2021-2022学年高一下学期数学沪教版(2020)必修第二册6.1.4 诱导公式(1)测试题word版含答案
文档属性
| 名称 | 2021-2022学年高一下学期数学沪教版(2020)必修第二册6.1.4 诱导公式(1)测试题word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 227.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 18:10:18 | ||
图片预览



文档简介
【学生版】
《第 6 章 三角》【6.1.4 诱导公式(1)】
一、选择题(每小题6分,共12分)
1、已知,则( )
A.0 B.m C.m D.不确定
【提示】
【答案】
【解析】
【考点】
2、已知,化简: ( )
A. B. C. D.随k的变化而变化
【提示】
【答案】
【解析】
【考点】
二、填充题(每小题10分,共60分)
3、化简:________
4、化简=
5、计算__________________
6、已知,则的值为
7、若,则等于
8、已知,且是第二象限角,则的值等于_______
三、解答题(第9题12分,第10题16分)
9、已知,
(1)求的值;
(2)求:的值;
9、(1)求函数的值域;
(2)化简:.
【附录】相关考点
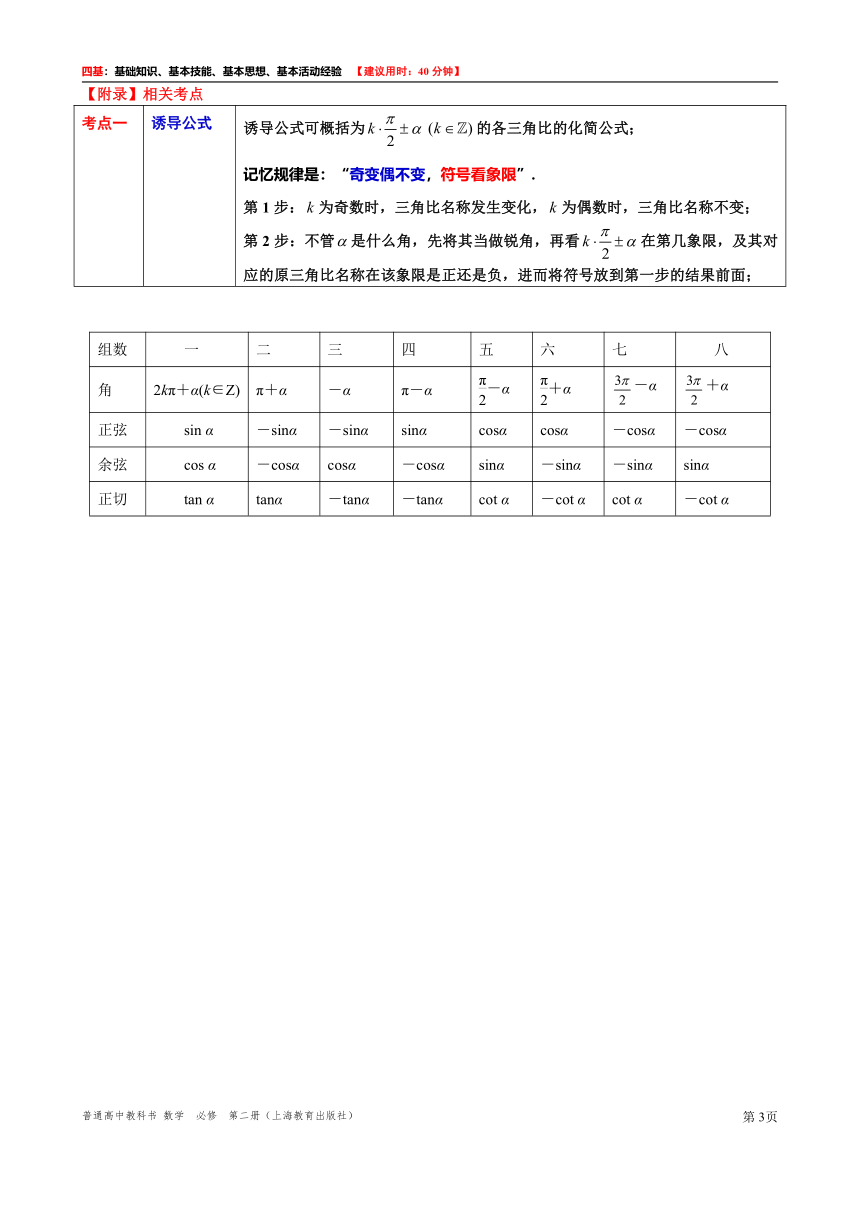
考点一 诱导公式 诱导公式可概括为的各三角比的化简公式; 记忆规律是:“奇变偶不变,符号看象限”. 第1步:为奇数时,三角比名称发生变化,为偶数时,三角比名称不变; 第2步:不管是什么角,先将其当做锐角,再看在第几象限,及其对应的原三角比名称在该象限是正还是负,进而将符号放到第一步的结果前面;
组数 一 二 三 四 五 六 七 八
角 2kπ+α(k∈Z) π+α -α π-α -α +α -α +α
正弦 sin α -sinα -sinα sinα cosα cosα -cosα -cosα
余弦 cos α -cosα cosα -cosα sinα -sinα -sinα sinα
正切 tan α tanα -tanα -tanα cot α -cot α cot α -cot α
【教师版】
《第 6 章 三角》【6.1.4 诱导公式(1)】
一、选择题(每小题6分,共12分)
1、已知,则( )
A.0 B.m C.m D.不确定
【提示】注意:;
【答案】C;
【解析】由;
【考点】诱导公式;
2、已知,化简: ( )
A. B. C. D.随k的变化而变化
【提示】根据给定条件按k是奇数和偶数分类,借助诱导公式化简计算;
【答案】B
【解析】因,则当k是奇数时,,
当k是偶数时,,
所以
故选:B
【考点】诱导公式;与分类讨论进行了简单整合;
二、填充题(每小题10分,共60分)
3、化简:________
【提示】注意:诱导公式的符号;
【答案】;
【解析】原式=;
【考点】诱导公式;
4、化简=
【提示】注意:诱导公式的符号;
【答案】;
【解析】;
【考点】诱导公式;
5、计算__________________
【提示】利用诱导公式变形给定表达式,再经计算;
【答案】0;
【解析】因,于是得:
原式
;
【考点】诱导公式;注意:角度之间的关系,创设条件使用诱导公式;
6、已知,则的值为
【提示】注意:诱导公式与同角三角函数公式的交汇;
【答案】;
【解析】根据诱导公式得,即,
又,所以,;
【考点】诱导公式;注意:与同角三角比的交汇;
7、若,则等于
【提示】注意:利用诱导公式化简;
【答案】;
【解析】因为,根据条件得,
又,所以;
所以,所以;
【考点】诱导公式;注意:与同角三角比的交汇;
8、已知,且是第二象限角,则的值等于_______
【提示】注意:利用诱导公式化简,再同角三角函数间的关系式可求得;
【答案】;
【解析】由,且是第二象限角,所以,,
所以,;故答案为:;
【考点】诱导公式;注意:与同角三角比的交汇;
三、解答题(第9题12分,第10题16分)
9、已知,
(1)求的值;
(2)求:的值;
【提示】(1)根据诱导公式即可求解;(2)根据诱导公式化简结合(1)的结论求值;
【答案】(1)3;(2)-4;
【解析】(1)由题:,所以,;
(2)
;
【考点】诱导公式的综合使用;
9、(1)求函数的值域;
(2)化简:.
【提示】(1)根据各象限三角函数的符号计算可得;(2)利用诱导公式及同角三角函数的基本关系化简;
【答案】(1);(2);;
【解析】(1)因为,显然;
当在第一象限时,、、,,所以;
当在第二象限时,、、,,
所以;
当在第三象限时,、、,,
所以;
当在第四象限时,、、,,
所以;
综上可得;
(2)
;
【考点】诱导公式与三角比符号的综合使用;
【附录】相关考点
考点一 诱导公式 诱导公式可概括为的各三角比的化简公式; 记忆规律是:“奇变偶不变,符号看象限”. 第1步:为奇数时,三角比名称发生变化,为偶数时,三角比名称不变; 第2步:不管是什么角,先将其当做锐角,再看在第几象限,及其对应的原三角比名称在该象限是正还是负,进而将符号放到第一步的结果前面;
组数 一 二 三 四 五 六 七 八
角 2kπ+α(k∈Z) π+α -α π-α -α +α -α +α
正弦 sin α -sinα -sinα sinα cosα cosα -cosα -cosα
余弦 cos α -cosα cosα -cosα sinα -sinα -sinα sinα
正切 tan α tanα -tanα -tanα cot α -cot α cot α -cot α
四基:基础知识、基本技能、基本思想、基本活动经验 【建议用时:40分钟】
第1页
普通高中教科书 数学 必修 第二册(上海教育出版社)
《第 6 章 三角》【6.1.4 诱导公式(1)】
一、选择题(每小题6分,共12分)
1、已知,则( )
A.0 B.m C.m D.不确定
【提示】
【答案】
【解析】
【考点】
2、已知,化简: ( )
A. B. C. D.随k的变化而变化
【提示】
【答案】
【解析】
【考点】
二、填充题(每小题10分,共60分)
3、化简:________
4、化简=
5、计算__________________
6、已知,则的值为
7、若,则等于
8、已知,且是第二象限角,则的值等于_______
三、解答题(第9题12分,第10题16分)
9、已知,
(1)求的值;
(2)求:的值;
9、(1)求函数的值域;
(2)化简:.
【附录】相关考点
考点一 诱导公式 诱导公式可概括为的各三角比的化简公式; 记忆规律是:“奇变偶不变,符号看象限”. 第1步:为奇数时,三角比名称发生变化,为偶数时,三角比名称不变; 第2步:不管是什么角,先将其当做锐角,再看在第几象限,及其对应的原三角比名称在该象限是正还是负,进而将符号放到第一步的结果前面;
组数 一 二 三 四 五 六 七 八
角 2kπ+α(k∈Z) π+α -α π-α -α +α -α +α
正弦 sin α -sinα -sinα sinα cosα cosα -cosα -cosα
余弦 cos α -cosα cosα -cosα sinα -sinα -sinα sinα
正切 tan α tanα -tanα -tanα cot α -cot α cot α -cot α
【教师版】
《第 6 章 三角》【6.1.4 诱导公式(1)】
一、选择题(每小题6分,共12分)
1、已知,则( )
A.0 B.m C.m D.不确定
【提示】注意:;
【答案】C;
【解析】由;
【考点】诱导公式;
2、已知,化简: ( )
A. B. C. D.随k的变化而变化
【提示】根据给定条件按k是奇数和偶数分类,借助诱导公式化简计算;
【答案】B
【解析】因,则当k是奇数时,,
当k是偶数时,,
所以
故选:B
【考点】诱导公式;与分类讨论进行了简单整合;
二、填充题(每小题10分,共60分)
3、化简:________
【提示】注意:诱导公式的符号;
【答案】;
【解析】原式=;
【考点】诱导公式;
4、化简=
【提示】注意:诱导公式的符号;
【答案】;
【解析】;
【考点】诱导公式;
5、计算__________________
【提示】利用诱导公式变形给定表达式,再经计算;
【答案】0;
【解析】因,于是得:
原式
;
【考点】诱导公式;注意:角度之间的关系,创设条件使用诱导公式;
6、已知,则的值为
【提示】注意:诱导公式与同角三角函数公式的交汇;
【答案】;
【解析】根据诱导公式得,即,
又,所以,;
【考点】诱导公式;注意:与同角三角比的交汇;
7、若,则等于
【提示】注意:利用诱导公式化简;
【答案】;
【解析】因为,根据条件得,
又,所以;
所以,所以;
【考点】诱导公式;注意:与同角三角比的交汇;
8、已知,且是第二象限角,则的值等于_______
【提示】注意:利用诱导公式化简,再同角三角函数间的关系式可求得;
【答案】;
【解析】由,且是第二象限角,所以,,
所以,;故答案为:;
【考点】诱导公式;注意:与同角三角比的交汇;
三、解答题(第9题12分,第10题16分)
9、已知,
(1)求的值;
(2)求:的值;
【提示】(1)根据诱导公式即可求解;(2)根据诱导公式化简结合(1)的结论求值;
【答案】(1)3;(2)-4;
【解析】(1)由题:,所以,;
(2)
;
【考点】诱导公式的综合使用;
9、(1)求函数的值域;
(2)化简:.
【提示】(1)根据各象限三角函数的符号计算可得;(2)利用诱导公式及同角三角函数的基本关系化简;
【答案】(1);(2);;
【解析】(1)因为,显然;
当在第一象限时,、、,,所以;
当在第二象限时,、、,,
所以;
当在第三象限时,、、,,
所以;
当在第四象限时,、、,,
所以;
综上可得;
(2)
;
【考点】诱导公式与三角比符号的综合使用;
【附录】相关考点
考点一 诱导公式 诱导公式可概括为的各三角比的化简公式; 记忆规律是:“奇变偶不变,符号看象限”. 第1步:为奇数时,三角比名称发生变化,为偶数时,三角比名称不变; 第2步:不管是什么角,先将其当做锐角,再看在第几象限,及其对应的原三角比名称在该象限是正还是负,进而将符号放到第一步的结果前面;
组数 一 二 三 四 五 六 七 八
角 2kπ+α(k∈Z) π+α -α π-α -α +α -α +α
正弦 sin α -sinα -sinα sinα cosα cosα -cosα -cosα
余弦 cos α -cosα cosα -cosα sinα -sinα -sinα sinα
正切 tan α tanα -tanα -tanα cot α -cot α cot α -cot α
四基:基础知识、基本技能、基本思想、基本活动经验 【建议用时:40分钟】
第1页
普通高中教科书 数学 必修 第二册(上海教育出版社)
