九年级同步导学案22.1.2二次函数y=ax2的图像和性质学案(无答案)
文档属性
| 名称 | 九年级同步导学案22.1.2二次函数y=ax2的图像和性质学案(无答案) | 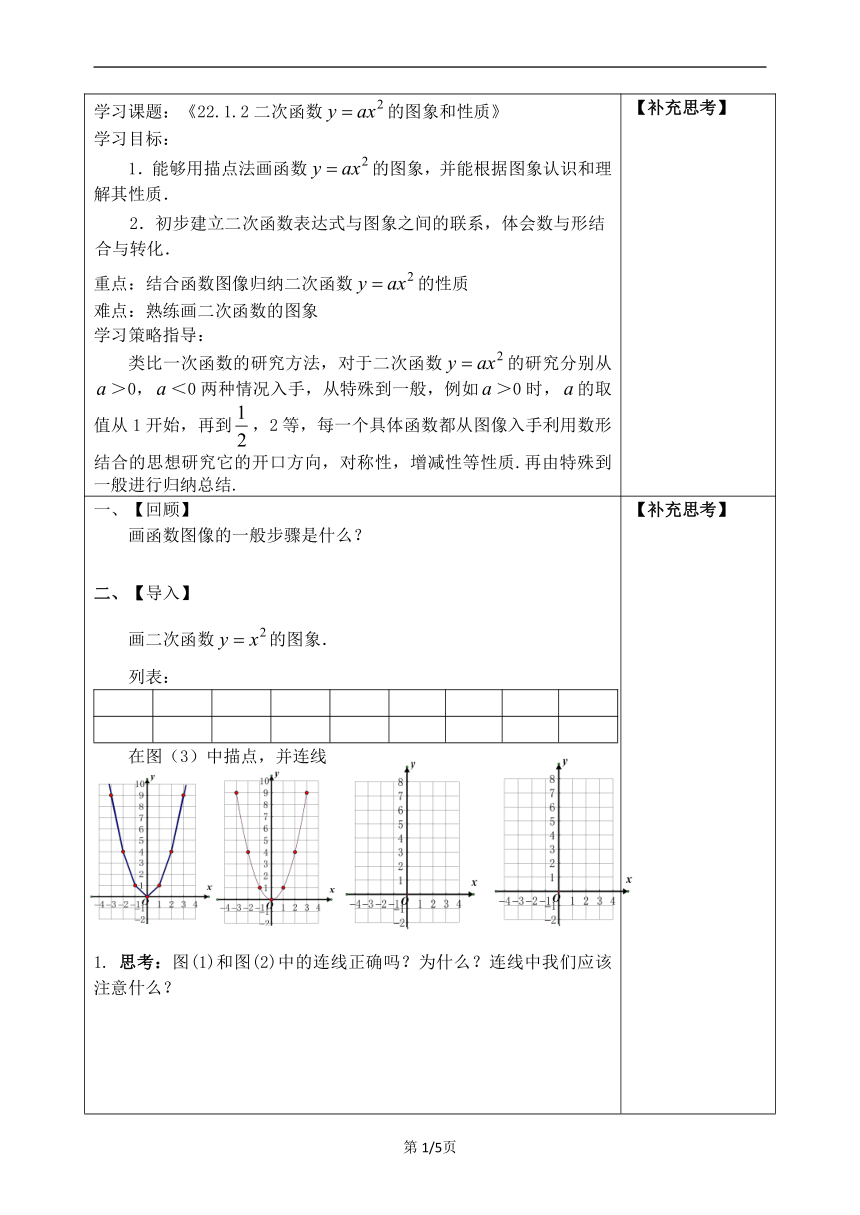 | |
| 格式 | doc | ||
| 文件大小 | 404.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览


文档简介
学习课题:《22.1.2二次函数的图象和性质》学习目标:1.能够用描点法画函数的图象,并能根据图象认识和理解其性质.2.初步建立二次函数表达式与图象之间的联系,体会数与形结合与转化.重点:结合函数图像归纳二次函数的性质难点:熟练画二次函数的图象学习策略指导:类比一次函数的研究方法,对于二次函数的研究分别从>0,<0两种情况入手,从特殊到一般,例如>0时,的取值从1开始,再到,2等,每一个具体函数都从图像入手利用数形结合的思想研究它的开口方向,对称性,增减性等性质.再由特殊到一般进行归纳总结. 【补充思考】
3 …
… …
归纳:抛物线的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”);在对称轴左侧,随的增大而 ,在对称轴右侧,随的增大而 ;越大,抛物线开口越 .猜测(可通过画图验证):二次函数的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”);在对称轴左侧,随的增大而 ,在对称轴右侧,随的增大而 ;越大,抛物线开口越 .归纳总结:一般地,的对称轴是 ,即直线= ,顶点是 .当>0时,抛物线开口 ;顶点是抛物线的最 点;在对称轴左侧(<0),随的增大而 ;在对称轴右侧(>0),随的增大而 .当<0时,抛物线开口 ,顶点是抛物线的最 点;在对称轴左侧(<0),随的增大而 ;在对称轴右侧(>0),随的增大而 .越大,抛物线的开口越 .四、【巩固】1.说出下列抛物线的开口方向、对称轴和顶点坐标:2.两条抛物线与在同一坐标系内,下列说法中不正确的是( )A.顶点相同 B.对称轴相同 C.开口方向相反 D.都有最小值3.函数是二次函数,则下列关于它的图象的说法:①开口向上;②开口向下;③对称轴是轴;④顶点坐标是(0,0);⑤顶点坐标是(0,-4);⑥顶点坐标是(-4,0);⑦有最高点;⑧有最低点.其中正确的有( )A.3个 B.4个 C.5个 D.6个4.若抛物线开口向下,则的值是( )A.-1或2 B.1或-2 C.2 D.-15.若二次函数的图象经过点P(,2),则该图象必经过点( )A.(,-2) B.(2,) C.(2,) D.(,2)五、【感悟】 1.本节课,我们主要学习哪些内容?2.在学习二次函数的图象和性质时,我们需要注意什么问题? 【补充思考】【补充思考】
六、【检测】1.函数的图象开口向_______,顶点是__________,对称轴是________,当=___________时,有最_________值是_________.2.二次函数有最低点,则=___________.3.写出一个过点(1,2)的函数表达式_________________.4.若二次函数的图象过点(1,-2),则的值是___________.5.二次函数的图象开口向下,则____________.6.已知函数是关于的二次函数.(1)求满足条件的的值;(2)当为何值时,抛物线有最低点?求这个最低点;(3)当为何值时,随的增大而增大?当为何值时,随的增大而减小?7.已知函数是二次函数,且开口向上.求的值及二次 函数的解析式,并回答随的变化规律.8.在同一直角坐标系中,抛物线与抛物线的形状______,开口方向____,两条抛物线关于_______对称.9.点在二次函数图像上,当>>0时,与的大小关系是____________.10.二次函数(>0),A(-2,),B(3,)在函数图像上,则_____.
七、【作业】
A组:
1.下列关于二次函数y=x2图象的说法中,错误的是( )
A.图象的形状是一条抛物线
B.图象开口向上,且关于y轴对称
C.图象的顶点是抛物线的最高点
D.图象的顶点坐标是(0,0)
2.两条抛物线y=5x2和y=﹣5x2在同一坐标系内,下列说法中不正确的是( )
A.顶点坐标相同 B.对称轴相同
C.开口方向相反 D.都有最小值
3.如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B. C. D.
4.在二次函数的图象的对称轴左侧,y随x的增大而增大,则m的值为 .
5.已知二次函数的图象经过点.
(1)求这个二次函数的解析式并画出其图象;
(2)请说出这个二次函数图象的顶点坐标、对称轴.
B组:
6.下列关于函数y=-x2的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点坐标为(0,0),其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点( )
A.(4,-2) B.(-4,2) C.(-2,-4) D.(2,4)
8.已知是二次函数,且函数图象有最高点.
(1)求k的值;
(2)求顶点坐标和对称轴.
PAGE
第2/5页
3 …
… …
归纳:抛物线的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”);在对称轴左侧,随的增大而 ,在对称轴右侧,随的增大而 ;越大,抛物线开口越 .猜测(可通过画图验证):二次函数的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”);在对称轴左侧,随的增大而 ,在对称轴右侧,随的增大而 ;越大,抛物线开口越 .归纳总结:一般地,的对称轴是 ,即直线= ,顶点是 .当>0时,抛物线开口 ;顶点是抛物线的最 点;在对称轴左侧(<0),随的增大而 ;在对称轴右侧(>0),随的增大而 .当<0时,抛物线开口 ,顶点是抛物线的最 点;在对称轴左侧(<0),随的增大而 ;在对称轴右侧(>0),随的增大而 .越大,抛物线的开口越 .四、【巩固】1.说出下列抛物线的开口方向、对称轴和顶点坐标:2.两条抛物线与在同一坐标系内,下列说法中不正确的是( )A.顶点相同 B.对称轴相同 C.开口方向相反 D.都有最小值3.函数是二次函数,则下列关于它的图象的说法:①开口向上;②开口向下;③对称轴是轴;④顶点坐标是(0,0);⑤顶点坐标是(0,-4);⑥顶点坐标是(-4,0);⑦有最高点;⑧有最低点.其中正确的有( )A.3个 B.4个 C.5个 D.6个4.若抛物线开口向下,则的值是( )A.-1或2 B.1或-2 C.2 D.-15.若二次函数的图象经过点P(,2),则该图象必经过点( )A.(,-2) B.(2,) C.(2,) D.(,2)五、【感悟】 1.本节课,我们主要学习哪些内容?2.在学习二次函数的图象和性质时,我们需要注意什么问题? 【补充思考】【补充思考】
六、【检测】1.函数的图象开口向_______,顶点是__________,对称轴是________,当=___________时,有最_________值是_________.2.二次函数有最低点,则=___________.3.写出一个过点(1,2)的函数表达式_________________.4.若二次函数的图象过点(1,-2),则的值是___________.5.二次函数的图象开口向下,则____________.6.已知函数是关于的二次函数.(1)求满足条件的的值;(2)当为何值时,抛物线有最低点?求这个最低点;(3)当为何值时,随的增大而增大?当为何值时,随的增大而减小?7.已知函数是二次函数,且开口向上.求的值及二次 函数的解析式,并回答随的变化规律.8.在同一直角坐标系中,抛物线与抛物线的形状______,开口方向____,两条抛物线关于_______对称.9.点在二次函数图像上,当>>0时,与的大小关系是____________.10.二次函数(>0),A(-2,),B(3,)在函数图像上,则_____.
七、【作业】
A组:
1.下列关于二次函数y=x2图象的说法中,错误的是( )
A.图象的形状是一条抛物线
B.图象开口向上,且关于y轴对称
C.图象的顶点是抛物线的最高点
D.图象的顶点坐标是(0,0)
2.两条抛物线y=5x2和y=﹣5x2在同一坐标系内,下列说法中不正确的是( )
A.顶点坐标相同 B.对称轴相同
C.开口方向相反 D.都有最小值
3.如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B. C. D.
4.在二次函数的图象的对称轴左侧,y随x的增大而增大,则m的值为 .
5.已知二次函数的图象经过点.
(1)求这个二次函数的解析式并画出其图象;
(2)请说出这个二次函数图象的顶点坐标、对称轴.
B组:
6.下列关于函数y=-x2的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点坐标为(0,0),其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点( )
A.(4,-2) B.(-4,2) C.(-2,-4) D.(2,4)
8.已知是二次函数,且函数图象有最高点.
(1)求k的值;
(2)求顶点坐标和对称轴.
PAGE
第2/5页
同课章节目录
