同步导学案23.1图形的旋转1(无答案)
文档属性
| 名称 | 同步导学案23.1图形的旋转1(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 182.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览


文档简介
学习课题:《23.1图形的旋转(第1课时)》学习目标:1.明确旋转及其旋转中心和旋转角的概念;2.知道旋转的三个性质.重点知识:旋转的基本性质.难点问题:图形的旋转的基本性质及其应用. 学习策略指导:“图形的旋转”作为小学数学新课程教材中的一部分,是图形变换中的一个非常重要的内容.再加上这部分课程内容丰富、灵活,能够使学生通过学习增强空间观念,进一步发展形象思维.在中学阶段已经学移,并且知道平移有两要素,通过比较大家就会猜想旋转需要满足哪些条件,从而激发学习的兴趣和动力. 【补充思考】
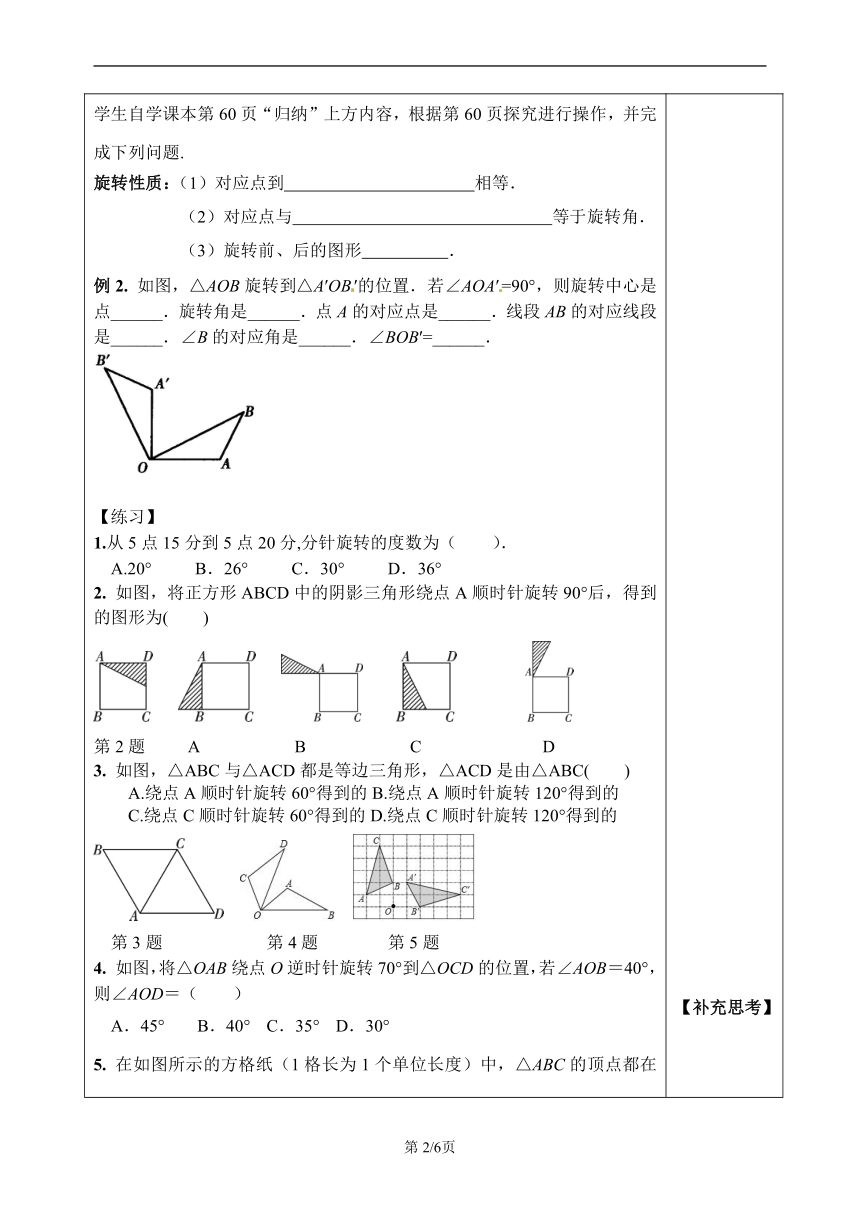
【回顾】1.下列现象不属于平移的是( )A.小华乘电梯从一楼到五楼 B.足球在操场上沿直线滚动 C.气球沿直线上升 D.雨滴沿直线从高空落下2.视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )A. B. C. D.【探究一】学生自学课本第59页内容,并完成下列问题.旋转定义:把一个平面图形绕着平面内某______沿着某个方向转动______的图形变换叫做旋转.这个点O叫做______,转动的角叫做______.如果图形上的点P经过旋转变为点P′,那么这两点叫做这个旋转的______.思考:旋转的三要素是 .例1.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.属于旋转的有( )A.2个 B.3个 C.4个 D.5个【探究二】学生自学课本第60页“归纳”上方内容,根据第60页探究进行操作,并完成下列问题.旋转性质:(1)对应点到 相等.(2)对应点与 等于旋转角.(3)旋转前、后的图形 .例2. 如图,△AOB旋转到△A′OB′的位置.若∠AOA′=90°,则旋转中心是点______.旋转角是______.点A的对应点是______.线段AB的对应线段是______.∠B的对应角是______.∠BOB′=______. 【练习】1.从5点15分到5点20分,分针旋转的度数为( ).A.20° B.26° C.30° D.36°2. 如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( ) 第2题 A B C D3. 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( ) A.绕点A顺时针旋转60°得到的B.绕点A顺时针旋转120°得到的C.绕点C顺时针旋转60°得到的D.绕点C顺时针旋转120°得到的 第3题 第4题 第5题4. 如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )A.45° B.40° C.35° D.30°5. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .90°6.如下图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.(1)在如图7所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置 (2)指出如图7所示中的线段BE与DF之间的关系. 【感悟】对于本节课你还有哪些困惑?在思想方法或知识上有哪些收获? 【补充思考】
【补充思考】【补充思考】【补充思考】
【检测】1. 将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )A. B. C. D.2. 如图,将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,则下列结论不一定成立的是( )A.∠ABC=∠ADE B.BC=DE C.BC∥AE D.AC平分∠BAE 第2题 第3题 第4题3. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为( )AA.1.6 B.1.8 C.2 D.2.64. 如图,将△ABC绕点B顺时针旋转得到△A'BC',使点A'落在AC上,已知∠C=40°,AC∥BC',则∠A= 度.5. 在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.(1)若AC=4,求DE的值;(2)确定△ACD的形状,并说明理由.【作业】A组1. 下面摆放的图案,从第二个起,每个都是前一个按顺时针方向旋转90°得到,第2019个图案中箭头的指向是( )A.上方 B.右方 C.下方 D.左方2. 如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转α角度(0<α<180°)得到△ADE,若DE∥AB,则α的值为( )A.65° B.75° C.85° D.130° 第2题 第3题 第6题 第7题3. 如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( )A.50° B.70° C.110° D.120°4. 时针从钟面上2点旋转到6点,共旋转了 度.5. 如图,正方形ABCD的边长为4,E是边BC上的一点,把△ABE平移到△DCF,再把△ABE逆时针旋转到△ADG的位置.(1)把△ABE逆时针旋转到△ADG的位置,旋转中心是 点;(2)若连接EG,求证:△AEG是等腰直角三角形. 第5题B组6. 如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA连续翻转(小正方形起始位置在AB边上),那么这个小正方形翻转到DA边的终点位置时,它的方向是( )A. B. C. D.7. 如图,在正方形ABCD中,点E在边DC上,DE=7,EC=3,把线段AE绕点A旋转后使点E落在直线BC上的点P处,则CP的长为________.3或178. 已知△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,点D是BC的中点,连接AE,BF.(1)当点A,C分别在DF和DE上时,如图1,试猜想线段AE和BF的数量关系,请直接写出你得到的结论(不要求证明)(2)将△DEF绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图2,请问:(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由. 第8题
PAGE
第1/6页
【回顾】1.下列现象不属于平移的是( )A.小华乘电梯从一楼到五楼 B.足球在操场上沿直线滚动 C.气球沿直线上升 D.雨滴沿直线从高空落下2.视力表中的字母“E”有各种不同的摆放形式,下面每种组合中的两个字母“E”不能关于某条直线成轴对称的是( )A. B. C. D.【探究一】学生自学课本第59页内容,并完成下列问题.旋转定义:把一个平面图形绕着平面内某______沿着某个方向转动______的图形变换叫做旋转.这个点O叫做______,转动的角叫做______.如果图形上的点P经过旋转变为点P′,那么这两点叫做这个旋转的______.思考:旋转的三要素是 .例1.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.属于旋转的有( )A.2个 B.3个 C.4个 D.5个【探究二】学生自学课本第60页“归纳”上方内容,根据第60页探究进行操作,并完成下列问题.旋转性质:(1)对应点到 相等.(2)对应点与 等于旋转角.(3)旋转前、后的图形 .例2. 如图,△AOB旋转到△A′OB′的位置.若∠AOA′=90°,则旋转中心是点______.旋转角是______.点A的对应点是______.线段AB的对应线段是______.∠B的对应角是______.∠BOB′=______. 【练习】1.从5点15分到5点20分,分针旋转的度数为( ).A.20° B.26° C.30° D.36°2. 如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( ) 第2题 A B C D3. 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( ) A.绕点A顺时针旋转60°得到的B.绕点A顺时针旋转120°得到的C.绕点C顺时针旋转60°得到的D.绕点C顺时针旋转120°得到的 第3题 第4题 第5题4. 如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )A.45° B.40° C.35° D.30°5. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .90°6.如下图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.(1)在如图7所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置 (2)指出如图7所示中的线段BE与DF之间的关系. 【感悟】对于本节课你还有哪些困惑?在思想方法或知识上有哪些收获? 【补充思考】
【补充思考】【补充思考】【补充思考】
【检测】1. 将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )A. B. C. D.2. 如图,将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,则下列结论不一定成立的是( )A.∠ABC=∠ADE B.BC=DE C.BC∥AE D.AC平分∠BAE 第2题 第3题 第4题3. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为( )AA.1.6 B.1.8 C.2 D.2.64. 如图,将△ABC绕点B顺时针旋转得到△A'BC',使点A'落在AC上,已知∠C=40°,AC∥BC',则∠A= 度.5. 在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.(1)若AC=4,求DE的值;(2)确定△ACD的形状,并说明理由.【作业】A组1. 下面摆放的图案,从第二个起,每个都是前一个按顺时针方向旋转90°得到,第2019个图案中箭头的指向是( )A.上方 B.右方 C.下方 D.左方2. 如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转α角度(0<α<180°)得到△ADE,若DE∥AB,则α的值为( )A.65° B.75° C.85° D.130° 第2题 第3题 第6题 第7题3. 如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( )A.50° B.70° C.110° D.120°4. 时针从钟面上2点旋转到6点,共旋转了 度.5. 如图,正方形ABCD的边长为4,E是边BC上的一点,把△ABE平移到△DCF,再把△ABE逆时针旋转到△ADG的位置.(1)把△ABE逆时针旋转到△ADG的位置,旋转中心是 点;(2)若连接EG,求证:△AEG是等腰直角三角形. 第5题B组6. 如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA连续翻转(小正方形起始位置在AB边上),那么这个小正方形翻转到DA边的终点位置时,它的方向是( )A. B. C. D.7. 如图,在正方形ABCD中,点E在边DC上,DE=7,EC=3,把线段AE绕点A旋转后使点E落在直线BC上的点P处,则CP的长为________.3或178. 已知△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,点D是BC的中点,连接AE,BF.(1)当点A,C分别在DF和DE上时,如图1,试猜想线段AE和BF的数量关系,请直接写出你得到的结论(不要求证明)(2)将△DEF绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图2,请问:(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由. 第8题
PAGE
第1/6页
同课章节目录
