同步导学案23.1图形的旋转2(无答案)
文档属性
| 名称 | 同步导学案23.1图形的旋转2(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览


文档简介
学习课题:《23.1图形的旋转(第2课时)》学习目标:1.能够按要求画出简单平面图形旋转后的图形.2.能够确定旋转中心和旋转角.3.能在平面直角坐标系内求旋转后点的坐标. 重点知识:画出简单图形旋转后的图形.难点问题:观察图案中相邻的两个基本图形,确定旋转中心和旋转角.学习策略指导:上节课已经学习了图形的旋转和旋转的基本性质,我们可以利用旋转来自己设计漂亮的图案了 ,准备好作图工具. 【补充思考】
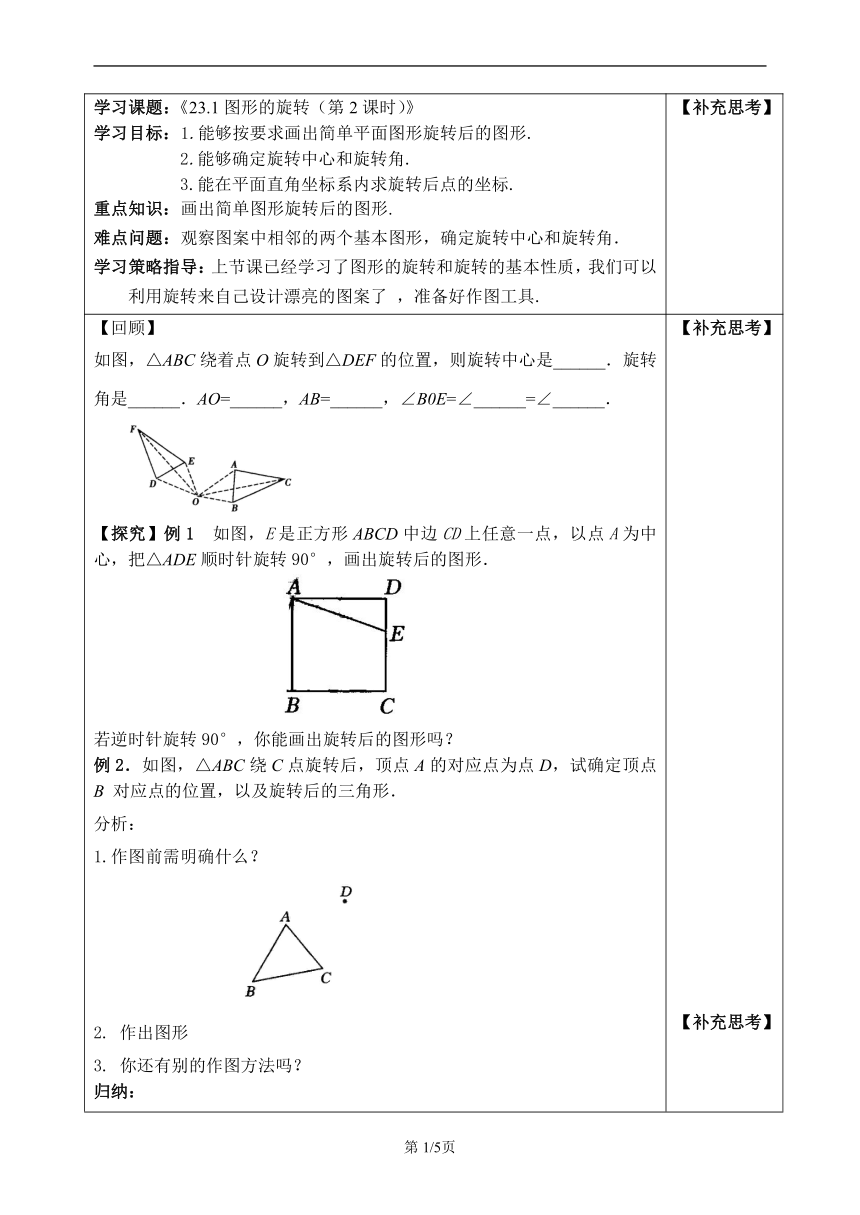
【回顾】如图,△ABC绕着点O旋转到△DEF的位置,则旋转中心是______.旋转角是______.AO=______,AB=______,∠B0E=∠______=∠______.【探究】例1 如图,E是正方形ABCD中边CD上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.若逆时针旋转90°,你能画出旋转后的图形吗?例2.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形.分析:1.作图前需明确什么? 2. 作出图形3. 你还有别的作图方法吗?归纳: 旋转作图时需确定:_______________________________. 旋转中心在_______________________________________.【练习】1.某商标标志如图所示,该标志的设计方案是( ) A.用一个菱形平移得到的B.用一个菱形经过两次旋转,每次旋转60°得到的C.用一个菱形经过两次旋转,每次旋转90°得到的D.用一个菱形经过两次旋转,每次旋转120°得到的 第1题 第2题 第3题 第4题2. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )A.30° B.90° C.120° D.180°3. 如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为( )A.(3,2) B.(3,﹣1) C.(2,﹣3) D.(3,﹣2)4.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转 次,每次旋转 度形成的.5.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).将△ABC绕原点O逆时针旋转90°后得得到△A1B1C1,请画出△A1B1C1.【感悟】对于本节课你还有哪些困惑?在思想方法或知识上有哪些收获? 【补充思考】【补充思考】
【检测】1.如图所示的图案是由下列哪个图形旋转得到的( )A. B. C. D.2. 以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为( )A.第一象限 B.第二象限 C.第三象限 D.第四象限3. 如图所示的图案,可以看作是由大写字母A绕中心连续旋转,每次旋转 度构成的. 第4题 第4题4. 如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC绕点P顺时针方向旋转90°,得到△A′B′C′,则点P的坐标为 . 5. 如图,在正方形网格中,以点A为旋转中心,将△ABC按逆时针方向旋转90°,画出旋转后的△AB1C1;【作业】A组1. 将如图方格纸中的图形绕O点顺时针旋转90°得到的图形是( )A. B.C.D..2. 下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度正确的是( )A.30° B.45° C.60° D.90°3. 下列3个图形中,能通过旋转得到右侧图形的有( )A.①② B.①③ C.②③ D.①②③4.一个等边三角形绕其中心至少旋转______度, 才能与自身重合.5. 以原点为中心,把点M (3,4)逆时针旋转90°得到点N,则点N的坐标为 .6. 如图,作以点O为旋转中心,把△ABC顺时针旋转120°后的△A′B′C′. 第6题B组7. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 . 第7题8. 将边长为2的正方形OABC如图①放置,O为坐标原点.(1) 如图②,若将正方形OABC绕点O逆时针旋转60°,求点A的坐标;(2) 如图③,若将图①中的正方形OABC绕点O逆时针旋转75°,求点B的坐标. 第8题
PAGE
第5/5页
【回顾】如图,△ABC绕着点O旋转到△DEF的位置,则旋转中心是______.旋转角是______.AO=______,AB=______,∠B0E=∠______=∠______.【探究】例1 如图,E是正方形ABCD中边CD上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.若逆时针旋转90°,你能画出旋转后的图形吗?例2.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形.分析:1.作图前需明确什么? 2. 作出图形3. 你还有别的作图方法吗?归纳: 旋转作图时需确定:_______________________________. 旋转中心在_______________________________________.【练习】1.某商标标志如图所示,该标志的设计方案是( ) A.用一个菱形平移得到的B.用一个菱形经过两次旋转,每次旋转60°得到的C.用一个菱形经过两次旋转,每次旋转90°得到的D.用一个菱形经过两次旋转,每次旋转120°得到的 第1题 第2题 第3题 第4题2. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )A.30° B.90° C.120° D.180°3. 如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为( )A.(3,2) B.(3,﹣1) C.(2,﹣3) D.(3,﹣2)4.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转 次,每次旋转 度形成的.5.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).将△ABC绕原点O逆时针旋转90°后得得到△A1B1C1,请画出△A1B1C1.【感悟】对于本节课你还有哪些困惑?在思想方法或知识上有哪些收获? 【补充思考】【补充思考】
【检测】1.如图所示的图案是由下列哪个图形旋转得到的( )A. B. C. D.2. 以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为( )A.第一象限 B.第二象限 C.第三象限 D.第四象限3. 如图所示的图案,可以看作是由大写字母A绕中心连续旋转,每次旋转 度构成的. 第4题 第4题4. 如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC绕点P顺时针方向旋转90°,得到△A′B′C′,则点P的坐标为 . 5. 如图,在正方形网格中,以点A为旋转中心,将△ABC按逆时针方向旋转90°,画出旋转后的△AB1C1;【作业】A组1. 将如图方格纸中的图形绕O点顺时针旋转90°得到的图形是( )A. B.C.D..2. 下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度正确的是( )A.30° B.45° C.60° D.90°3. 下列3个图形中,能通过旋转得到右侧图形的有( )A.①② B.①③ C.②③ D.①②③4.一个等边三角形绕其中心至少旋转______度, 才能与自身重合.5. 以原点为中心,把点M (3,4)逆时针旋转90°得到点N,则点N的坐标为 .6. 如图,作以点O为旋转中心,把△ABC顺时针旋转120°后的△A′B′C′. 第6题B组7. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 . 第7题8. 将边长为2的正方形OABC如图①放置,O为坐标原点.(1) 如图②,若将正方形OABC绕点O逆时针旋转60°,求点A的坐标;(2) 如图③,若将图①中的正方形OABC绕点O逆时针旋转75°,求点B的坐标. 第8题
PAGE
第5/5页
同课章节目录
