同步导学案23.2.2中心对称图形(无答案)
文档属性
| 名称 | 同步导学案23.2.2中心对称图形(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览

文档简介
学习课题:《23.2.2中心对称图形》学习目标:1.知道中心对称图形的概念及中心对称图形的对称中心的概念;2.会判断一个图形是否是中心对称图形;重点知识:中心对称图形的有关概念及其它们的运用.难点问题:区别关于中心对称的两个图形和中心对称图形.学习策略指导:本课采用“观察—操作—分析—归纳—应用”流程, 使学生进一步体验到数学是一个充满观察、实验、归纳、联想和猜测的探索过程.通过创设情境, 主动探究, 发挥同学们的主观能动性, 真正成为教学活动的主人. 【补充思考】
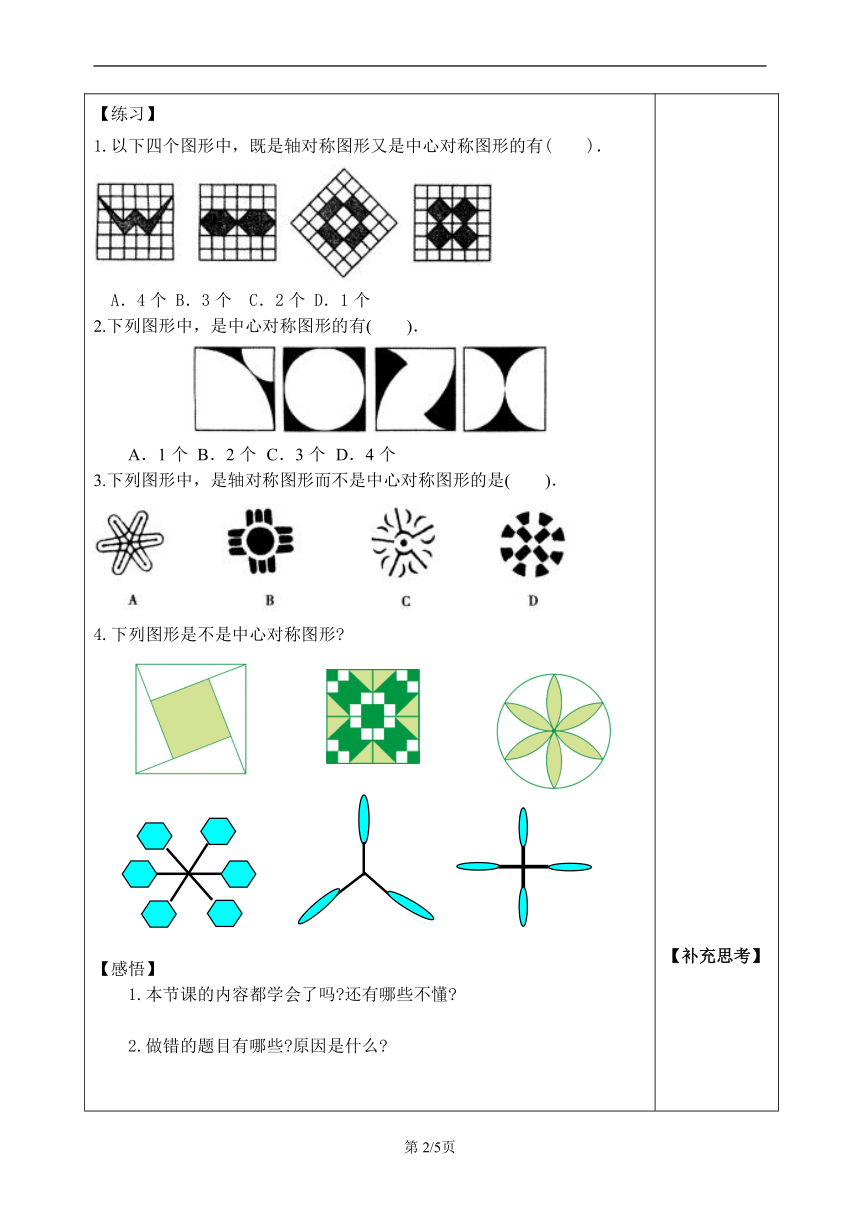
【回顾】什么是中心对称?它针对几个图形来说?【探究】自主学习(自学课本第66——第67页,完成下列各题)1.填一填①把一个图形绕着某一个点旋转______,如果旋转后的图形能够与原来的图形______,那么这个图形叫做中心对称图形,这个点就是它的____.②线段不仅是轴对称图形,而且是______图形,它的对称中心是________.③平行四边形是___________图形,它的对称中心是__________________.④圆不仅是轴对称图形,而且是________图形,它的对称中心是______.2.想一想.①说说中心对称图形与中心对称的联系与区别?②指出以下那个图形是中心对称图形,如果是的话,说出它的对称中心。①等边三角形 ②矩形 ③正方形 ④等腰三角形 ⑤菱形 ⑥正五边形⑦正六边形 【练习】1.以下四个图形中,既是轴对称图形又是中心对称图形的有( ).A.4个 B.3个 C.2个 D.1个 2.下列图形中,是中心对称图形的有( ). A.1个 B.2个 C.3个 D.4个3.下列图形中,是轴对称图形而不是中心对称图形的是( ). 4.下列图形是不是中心对称图形 【感悟】1.本节课的内容都学会了吗 还有哪些不懂 2.做错的题目有哪些 原因是什么 【检测】1.判断(1)中心对称图形只能有一个对称中心.( )(2)中心对称图形一定是轴对称图形.( )(3)中心对称图形的对称中心不可能在图形的外部.( )2.若两个图形关于某一点成中心对称,那么下列说法:①对称点的连线必过对称中心;②这两个图形一定全等;③对应线段一定平行且相等;④将一个图形绕对称中心旋转180°必定与另一个图形重合.其中正确的是( )(A) ①② (B) ①③ (C) ①②③ (D) ①②③④3.将两个大小相等的圆部分重合,其中重叠的部分(如图①中的阴影部分)我们称之为一个“花瓣”,由“花瓣”及圆组成的图形称之为花瓣图形,如图②是一些由“花瓣”和圆组成的图形.(1) 图②中是轴对称图形的有________,是中心对称图形的有________(填字母).(2) 若“花瓣”在圆中是均匀分布的,试根据(1)中的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)之间的规律.(3) 根据上面的结论,试判断下列花瓣图形的对称性:①九瓣图形是__________;②十二瓣图形是__________________________;③十五瓣图形是__________;④二十六瓣图形是__________________________.【作业】A组1. 近几年我国国产汽车行业蓬勃发展,下列汽车标识中,是中心对称图形的是( ) A B C D2. 如图①所示的四张牌,若将其中一张牌旋转180°后得到图②,则旋转的牌是( ) A B C D 第2题 第4题3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A.多边形 B.边数为奇数的正多边形C.正多边形 D.边数为偶数的正多边形4. 如图将①②③④中的一块涂成阴影能与图中原有阴影部分组成中心对称图形的是( )A.④ B.③ C.② D.①5. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:(1)使得6个阴影小等边三角形组成一个轴对称图形.(2)使得6个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形) 第5题B组6. 如图,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下列四个点M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是________. 第6题 第7题7. 如图是两个全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面的图案绕点O顺时针旋转,使得两个图案构成的图形是中心对称图形,那么它至少旋转________.8. 用六根一样长的小棒搭成如图所示的图形,试移动AC、BC这两根小棒,使六根小棒成为中心对称图形;若移动AC、DE这两根,能不能也达到要求呢?(画出图形) 第8题 【补充思考】
【补充思考】【补充思考】【补充思考】
PAGE
第5/5页
【回顾】什么是中心对称?它针对几个图形来说?【探究】自主学习(自学课本第66——第67页,完成下列各题)1.填一填①把一个图形绕着某一个点旋转______,如果旋转后的图形能够与原来的图形______,那么这个图形叫做中心对称图形,这个点就是它的____.②线段不仅是轴对称图形,而且是______图形,它的对称中心是________.③平行四边形是___________图形,它的对称中心是__________________.④圆不仅是轴对称图形,而且是________图形,它的对称中心是______.2.想一想.①说说中心对称图形与中心对称的联系与区别?②指出以下那个图形是中心对称图形,如果是的话,说出它的对称中心。①等边三角形 ②矩形 ③正方形 ④等腰三角形 ⑤菱形 ⑥正五边形⑦正六边形 【练习】1.以下四个图形中,既是轴对称图形又是中心对称图形的有( ).A.4个 B.3个 C.2个 D.1个 2.下列图形中,是中心对称图形的有( ). A.1个 B.2个 C.3个 D.4个3.下列图形中,是轴对称图形而不是中心对称图形的是( ). 4.下列图形是不是中心对称图形 【感悟】1.本节课的内容都学会了吗 还有哪些不懂 2.做错的题目有哪些 原因是什么 【检测】1.判断(1)中心对称图形只能有一个对称中心.( )(2)中心对称图形一定是轴对称图形.( )(3)中心对称图形的对称中心不可能在图形的外部.( )2.若两个图形关于某一点成中心对称,那么下列说法:①对称点的连线必过对称中心;②这两个图形一定全等;③对应线段一定平行且相等;④将一个图形绕对称中心旋转180°必定与另一个图形重合.其中正确的是( )(A) ①② (B) ①③ (C) ①②③ (D) ①②③④3.将两个大小相等的圆部分重合,其中重叠的部分(如图①中的阴影部分)我们称之为一个“花瓣”,由“花瓣”及圆组成的图形称之为花瓣图形,如图②是一些由“花瓣”和圆组成的图形.(1) 图②中是轴对称图形的有________,是中心对称图形的有________(填字母).(2) 若“花瓣”在圆中是均匀分布的,试根据(1)中的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)之间的规律.(3) 根据上面的结论,试判断下列花瓣图形的对称性:①九瓣图形是__________;②十二瓣图形是__________________________;③十五瓣图形是__________;④二十六瓣图形是__________________________.【作业】A组1. 近几年我国国产汽车行业蓬勃发展,下列汽车标识中,是中心对称图形的是( ) A B C D2. 如图①所示的四张牌,若将其中一张牌旋转180°后得到图②,则旋转的牌是( ) A B C D 第2题 第4题3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A.多边形 B.边数为奇数的正多边形C.正多边形 D.边数为偶数的正多边形4. 如图将①②③④中的一块涂成阴影能与图中原有阴影部分组成中心对称图形的是( )A.④ B.③ C.② D.①5. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:(1)使得6个阴影小等边三角形组成一个轴对称图形.(2)使得6个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形) 第5题B组6. 如图,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下列四个点M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是________. 第6题 第7题7. 如图是两个全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面的图案绕点O顺时针旋转,使得两个图案构成的图形是中心对称图形,那么它至少旋转________.8. 用六根一样长的小棒搭成如图所示的图形,试移动AC、BC这两根小棒,使六根小棒成为中心对称图形;若移动AC、DE这两根,能不能也达到要求呢?(画出图形) 第8题 【补充思考】
【补充思考】【补充思考】【补充思考】
PAGE
第5/5页
同课章节目录
