24.1.2垂直于弦的直径 同步导学案(无答案)
文档属性
| 名称 | 24.1.2垂直于弦的直径 同步导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 330.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 00:00:00 | ||
图片预览

文档简介
学习课题:《24.1.2垂直于弦的直径》学习目标:1.知道圆的轴对称性及对称轴.2. 知道垂径定理及其推论,并体会利用圆的对称性证明垂径定理;会用垂径定理解决有关的证明和计算问题.3. 经历探索垂径定理及其推论的过程,进一步体会研究几何图形的各种方法.重点知识:垂直于弦的直径的性质、推论及应用.难点问题:对垂直于弦的直径的性质、推论的说明理解.学习策略指导:本节课研究圆的轴对称性与垂径定理及其简单应用,垂径定理既是圆的性质的重要体现,是圆的轴对称性的具体化,也是今后证明线段相等、角相等、弧相等、垂直关系的重要依据.同时,也为进行圆的计算和作图提供了方法和依据.本节课通过“实验—观察—猜想—证明”的途径,进一步培养学生的动手、观察、分析、联想能力,同时利用圆的轴对称性,对学生进行数学美的教育. 【补充思考】
【回顾】1.如图:AB是⊙O的 ;CD是⊙O的 ;⊙O中优弧有 ;劣弧有 .2.在 圆或 圆中,能够 叫等弧.3.圆是轴对称图形吗?如果是,对称轴是什么?【导入】你知道赵州桥吗?它的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)是7.2m,能求出赵州桥主桥拱的半径吗?【探究】探究一:圆的轴对称性同学们能不能找到图1这个圆的圆心?拿出手中的圆形纸片试一试.问题:1.在找圆心的过程中,把圆纸片折叠时,两个半圆能够__________.2.刚才的实验能说明什么?由此你能得到什么结论?圆是____________,___________________________是它的对称抽,它的对称轴有 条.探究二:垂径定理如图2,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足E.1.这个图形是对称图形吗? 【补充思考】
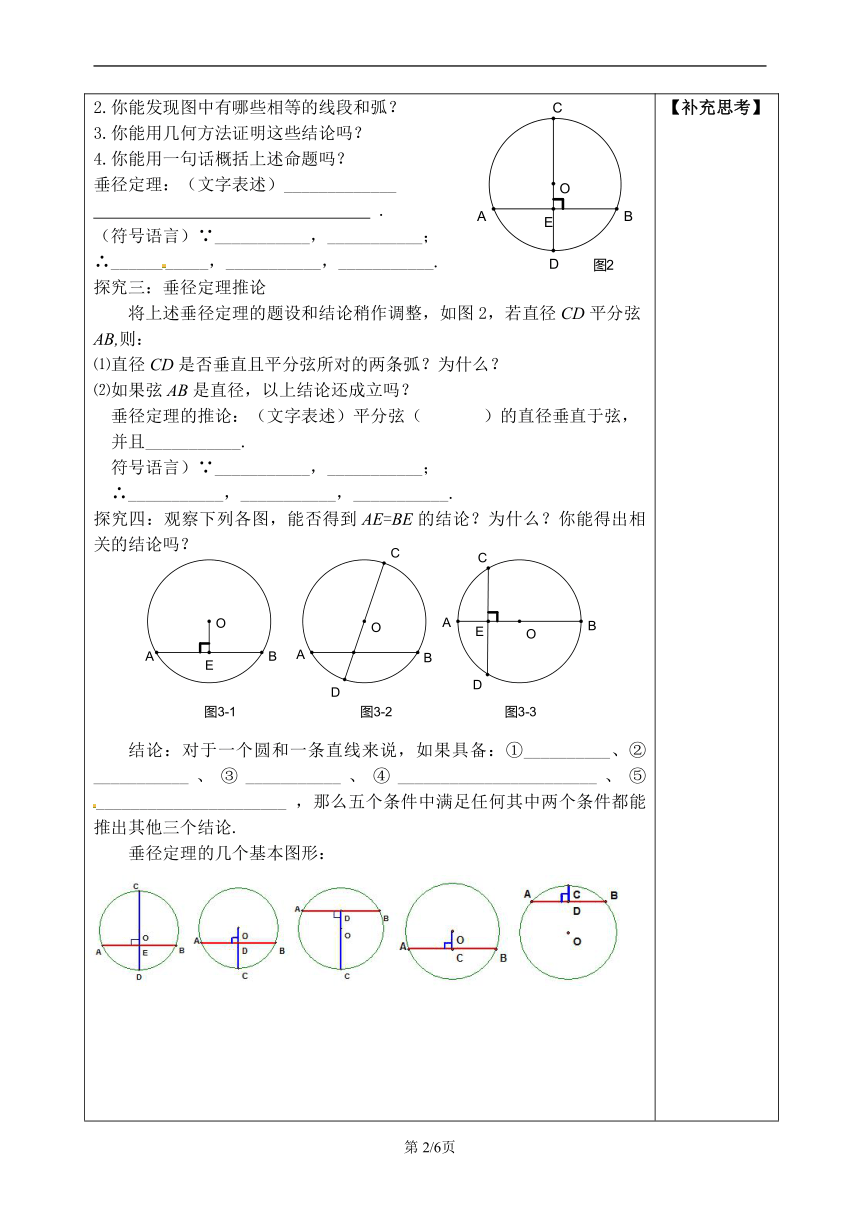
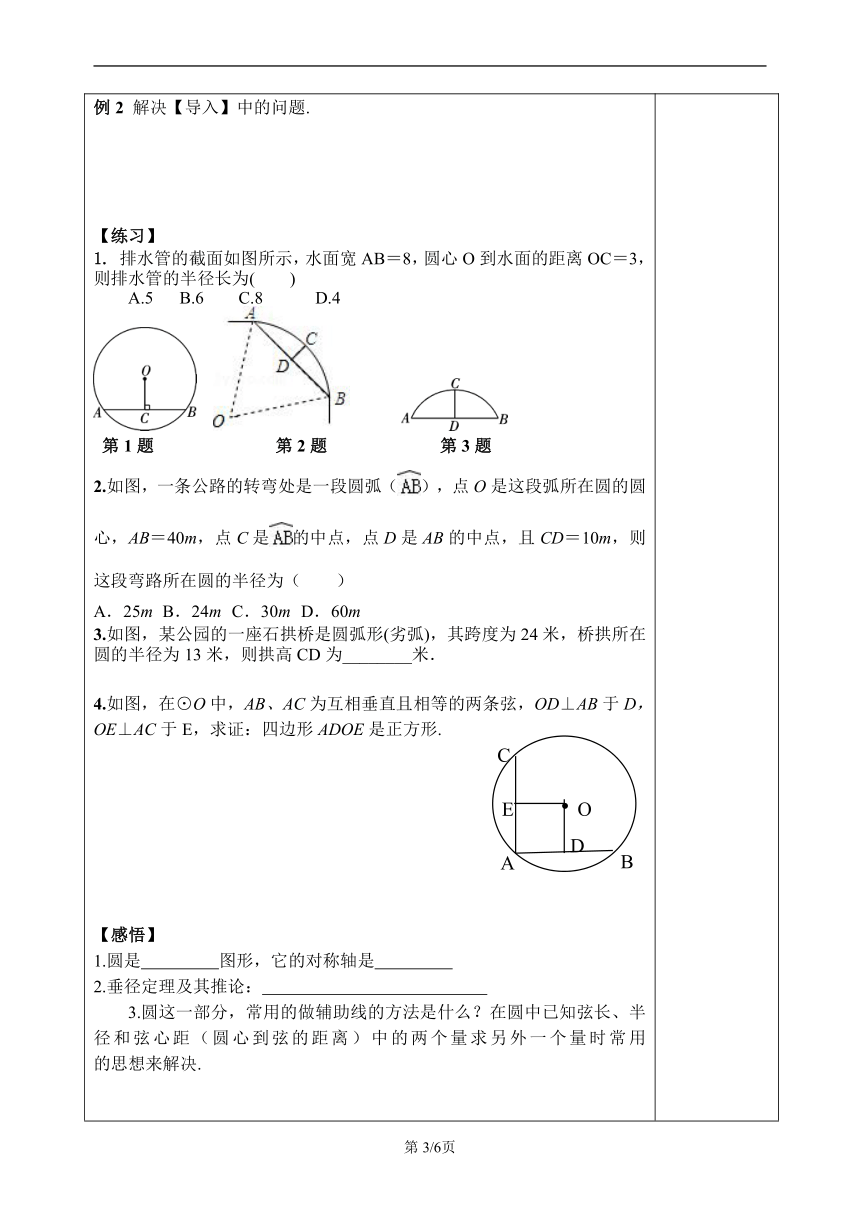
2.你能发现图中有哪些相等的线段和弧?3.你能用几何方法证明这些结论吗?4.你能用一句话概括上述命题吗?垂径定理:(文字表述)_____________ .(符号语言)∵___________,___________;∴___________,___________,___________.探究三:垂径定理推论将上述垂径定理的题设和结论稍作调整,如图2,若直径CD平分弦AB,则:⑴直径CD是否垂直且平分弦所对的两条弧?为什么?⑵如果弦AB是直径,以上结论还成立吗?垂径定理的推论:(文字表述)平分弦( )的直径垂直于弦,并且___________.符号语言)∵___________,___________;∴___________,___________,___________.探究四:观察下列各图,能否得到AE=BE的结论?为什么?你能得出相关的结论吗?结论:对于一个圆和一条直线来说,如果具备:①__________、②___________、③___________、④_______________________、⑤______________________ ,那么五个条件中满足任何其中两个条件都能推出其他三个结论.垂径定理的几个基本图形:例2 解决【导入】中的问题.【练习】1. 排水管的截面如图所示,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径长为( ) A.5 B.6 C.8 D.4 第1题 第2题 第3题2.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )A.25m B.24m C.30m D.60m3.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,桥拱所在圆的半径为13米,则拱高CD为________米.4.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.【感悟】1.圆是 图形,它的对称轴是 2.垂径定理及其推论: 3.圆这一部分,常用的做辅助线的方法是什么?在圆中已知弦长、半径和弦心距(圆心到弦的距离)中的两个量求另外一个量时常用 的思想来解决. 【补充思考】
【检测】1.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm。则直尺的宽是______.2.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________,最长弦长为_______.3.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是 .4.如图,已知半径为5的⊙O与y轴交于点M(0,-4),N(0,-10),函数(x<0)的图像过点P,则k=______.(第1题图 ) (第3题图) (第4题图) (第5题图) 5.在圆柱形油槽内装有一些油。截面如图,油面宽AB为6分米,如果再注入一些油 后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )A.6分米 B.8分米 C.10分米 D.12分米6.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.求证AC=BD.7.已知:如图,⊙O的直径AB=20cm,,求弦BC的长度.【作业】A组1. 如图,CD是⊙O的直径,弦AB⊥CD于点E,连接BC、BD,下列结论不一定正确的是( ) A. AE=BE B. = C. OE=DE D. = 第1题 第2题 第3题2. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE的长为( )A.8cm B.5cm C.3cm D.2cm3. 如图,⊙O的弦AB=6,C为AB的中点,且OC=4,则⊙O的半径为( )A.8 B.6 C.5 D.4 4. 如图,在⊙O中,∠OAB=45°,圆心O到弦AB的距离OE=2cm,则弦AB的长为________cm.5. 如图,P为⊙O内一点.(1) 过点P是否存在一条弦AB,使P为AB的中点?如果存在,请作出弦AB.(2) 在(1)的条件下,若⊙O的直径为16cm,OP=4cm,求弦AB的长. 第5题6.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施. 第6题B组7. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )A.2cm B.4cmC.2cm或4cm D.2cm或4cm8. 如图,点E在y轴上,⊙E与x轴交于点A,B,与y轴交于点C,D.若C(0,4),D(0,-1),则线段AB的长度为________.9. 已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm.求弦AB和CD之间的距离.
A
B
O
D
E
C
PAGE
第6/6页
【回顾】1.如图:AB是⊙O的 ;CD是⊙O的 ;⊙O中优弧有 ;劣弧有 .2.在 圆或 圆中,能够 叫等弧.3.圆是轴对称图形吗?如果是,对称轴是什么?【导入】你知道赵州桥吗?它的主桥拱是圆弧形,它的跨度(弧所对的弦长)是37.4m,拱高(弧的中点到弦的距离)是7.2m,能求出赵州桥主桥拱的半径吗?【探究】探究一:圆的轴对称性同学们能不能找到图1这个圆的圆心?拿出手中的圆形纸片试一试.问题:1.在找圆心的过程中,把圆纸片折叠时,两个半圆能够__________.2.刚才的实验能说明什么?由此你能得到什么结论?圆是____________,___________________________是它的对称抽,它的对称轴有 条.探究二:垂径定理如图2,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足E.1.这个图形是对称图形吗? 【补充思考】
2.你能发现图中有哪些相等的线段和弧?3.你能用几何方法证明这些结论吗?4.你能用一句话概括上述命题吗?垂径定理:(文字表述)_____________ .(符号语言)∵___________,___________;∴___________,___________,___________.探究三:垂径定理推论将上述垂径定理的题设和结论稍作调整,如图2,若直径CD平分弦AB,则:⑴直径CD是否垂直且平分弦所对的两条弧?为什么?⑵如果弦AB是直径,以上结论还成立吗?垂径定理的推论:(文字表述)平分弦( )的直径垂直于弦,并且___________.符号语言)∵___________,___________;∴___________,___________,___________.探究四:观察下列各图,能否得到AE=BE的结论?为什么?你能得出相关的结论吗?结论:对于一个圆和一条直线来说,如果具备:①__________、②___________、③___________、④_______________________、⑤______________________ ,那么五个条件中满足任何其中两个条件都能推出其他三个结论.垂径定理的几个基本图形:例2 解决【导入】中的问题.【练习】1. 排水管的截面如图所示,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径长为( ) A.5 B.6 C.8 D.4 第1题 第2题 第3题2.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )A.25m B.24m C.30m D.60m3.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,桥拱所在圆的半径为13米,则拱高CD为________米.4.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.【感悟】1.圆是 图形,它的对称轴是 2.垂径定理及其推论: 3.圆这一部分,常用的做辅助线的方法是什么?在圆中已知弦长、半径和弦心距(圆心到弦的距离)中的两个量求另外一个量时常用 的思想来解决. 【补充思考】
【检测】1.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm。则直尺的宽是______.2.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________,最长弦长为_______.3.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是 .4.如图,已知半径为5的⊙O与y轴交于点M(0,-4),N(0,-10),函数(x<0)的图像过点P,则k=______.(第1题图 ) (第3题图) (第4题图) (第5题图) 5.在圆柱形油槽内装有一些油。截面如图,油面宽AB为6分米,如果再注入一些油 后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )A.6分米 B.8分米 C.10分米 D.12分米6.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.求证AC=BD.7.已知:如图,⊙O的直径AB=20cm,,求弦BC的长度.【作业】A组1. 如图,CD是⊙O的直径,弦AB⊥CD于点E,连接BC、BD,下列结论不一定正确的是( ) A. AE=BE B. = C. OE=DE D. = 第1题 第2题 第3题2. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE的长为( )A.8cm B.5cm C.3cm D.2cm3. 如图,⊙O的弦AB=6,C为AB的中点,且OC=4,则⊙O的半径为( )A.8 B.6 C.5 D.4 4. 如图,在⊙O中,∠OAB=45°,圆心O到弦AB的距离OE=2cm,则弦AB的长为________cm.5. 如图,P为⊙O内一点.(1) 过点P是否存在一条弦AB,使P为AB的中点?如果存在,请作出弦AB.(2) 在(1)的条件下,若⊙O的直径为16cm,OP=4cm,求弦AB的长. 第5题6.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施. 第6题B组7. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )A.2cm B.4cmC.2cm或4cm D.2cm或4cm8. 如图,点E在y轴上,⊙E与x轴交于点A,B,与y轴交于点C,D.若C(0,4),D(0,-1),则线段AB的长度为________.9. 已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm.求弦AB和CD之间的距离.
A
B
O
D
E
C
PAGE
第6/6页
同课章节目录
