24.1.3弧、弦、圆心角 同步导学案(无答案)
文档属性
| 名称 | 24.1.3弧、弦、圆心角 同步导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 209.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览


文档简介
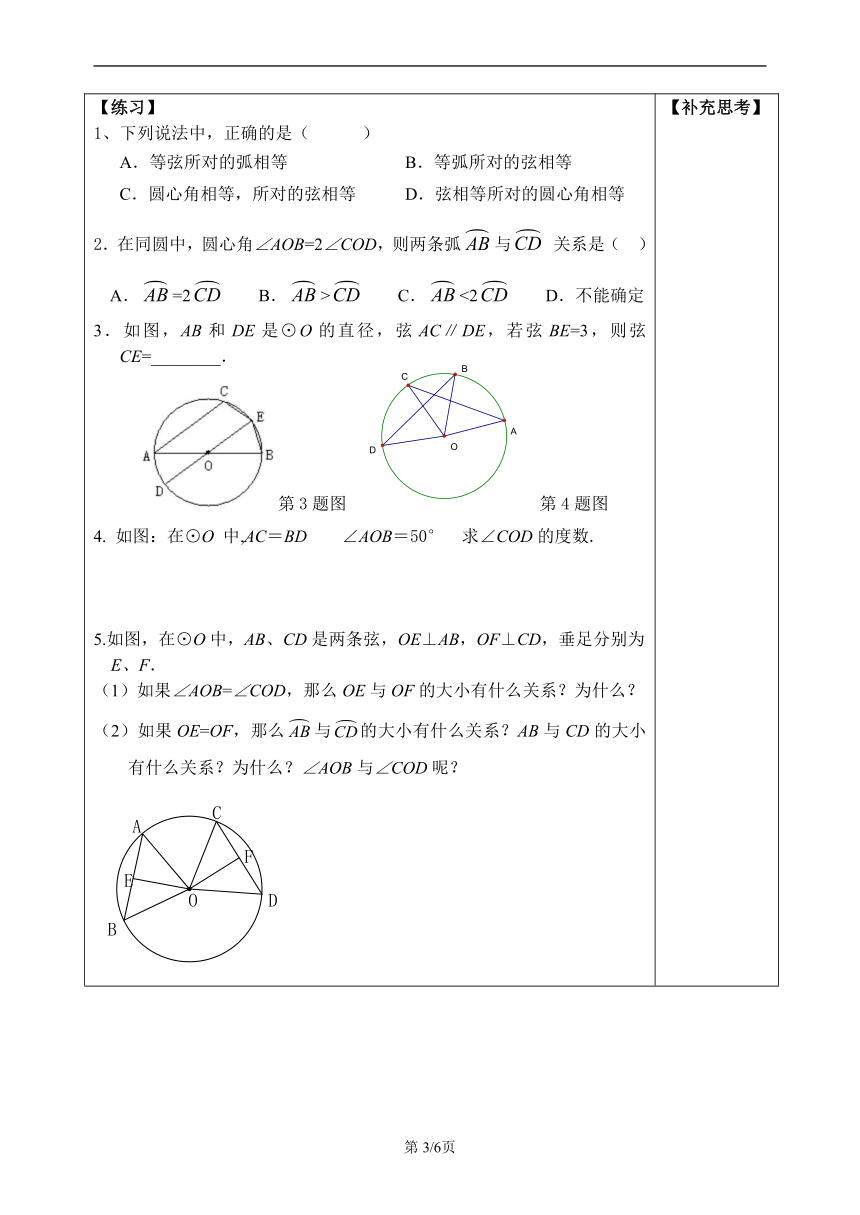
学习课题:《24.1.3弧、弦、圆心角》学习目标:1.在实际操作中发现圆的旋转不变性;2.会辨识圆心角;3.能利用圆心角、弧、弦之间的关系解决有关的证明与计算问题.重点知识:圆心角、弧、弦之间关系定理.难点问题:从圆的旋转不变性出发,得到圆心角、弧、弦之间的相等关系定理.学习策略指导:本节课主要研究圆心角、弧、弦之间的关系,并利用其解决相关问题,是在学生学习了圆的相关概念、垂径定理以及旋转的有关知识的基础上进行的,它是对前面所学知识的应用,也是证明同圆或等圆中弧相等、角相等以及线段相等的重要依据.此时的学生,已具有了一定的观察、实验、猜想、验证、推理、交流等数学能力,以及一定的合情推理和演绎推理的能力.本节课将采用动手操作、自主探究、合作交流相结合的方式进行学习,充分发挥学生的主体作用,使知识和能力得到内化.【回顾】1.圆是 对称图形,它的对称轴是 .2.圆是中心对称图形吗?它的对称中心在哪里?3.圆绕圆心旋转任意一个角度总能与原图形重合吗?【导入】圆是一个特殊的图形,通过前面的学习,同学们已经了解到圆既是一个轴对称图形又是一个中心对称图形.那么圆还有其他特性吗 【探究】探究一:圆心角定义1.如图,像∠AOB这样_________的角叫做圆心角.∠OAB与∠OBA是圆心角吗?为什么?2.∠AOB所对的弧为 ,所对的弦为 .3.弦AB所对的弧为 ,所对的圆心角为 .4. 所对的弦为 ,所对的圆心角为 .探究二:圆心角、弧、弦之间的关系按下面的步骤做一做:1.在两张透明纸上,作两个半径相等的⊙O和⊙O′,沿圆周分别将两圆剪下.2.在⊙O和⊙O′上,分别作相等的圆心角∠AOB和∠A′O′B′(如下图示),将两圆心重合并固定.注意:在画∠AOB与∠A′O′B′时,要使OB相对于OA的方向与O′B′相对于O′A′的方向一致,否则当OA与OA′重合时,OB与O′B′不能重合.3.将其中的一个圆旋转一个角度.使得OA与O′A′重合.由做一做知:在同圆等圆中,相等的圆心角所对的弧___,所对的弦也______. 在同圆等圆中,如果两条弧相等,那么它们所对的圆心角____,所对的弦 ;在同圆等圆中,如果两条弦相等,那么它们所对的圆心角____,所对的优弧和劣弧 ;归纳:在同圆等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也 .例1 如图,在⊙O中,AB、CD是两条弦,(1)如果AB=CD,那么_________,__________.(2)如果 ,那么_________,__________.(3)如果∠AOB=∠COD,那么_________,__________.(4),OE⊥AB,OF⊥CD,垂足分别为E、F.则OE____OF.证明你的结论.例2 如图,在⊙O中, = ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC. 【练习】1、下列说法中,正确的是( )A.等弦所对的弧相等 B.等弧所对的弦相等C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等2.在同圆中,圆心角∠AOB=2∠COD,则两条弧与 关系是( ) A.=2 B.> C.<2 D.不能确定3.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.第3题图 第4题图 4. 如图:在⊙O 中,AC=BD ∠AOB=50° 求∠COD的度数. 5.如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E、F.(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?(2)如果OE=OF,那么与的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢? ( http: / / www..cn ) 【补充思考】【补充思考】【补充思考】【补充思考】
【感悟】1. 是圆心角;2.圆不仅是 对称图形,而且是 对称图形,对称中心是 .3.弧、弦、圆心角之间的关系定理: .在关系定理中,为什么要说“同圆或等圆”?能不能去掉?在证明圆中弧、弦、圆心角相等时,可以通过证明本量中以外的量相等的来实现. 【补充思考】
【检测】1.如果两个圆心角相等,那么( )A.这两个圆心角所对的弦相等; B.这两个圆心角所对的弧相等;C.这两个圆心角所对的弦的弦心距(圆心到弦的距离)相等; D.以上说法都不对2.如图1,⊙O中,如果=2,那么( ).A.AB=2AC B.AB=AC C.AB<2AC D.AB>2AC 图1 图2 图3 图43.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.4.已知:如图2,已知AB和CD是⊙O的两条直径,弦CE∥AB,求证: = 5.如图3,在⊙O中,弦AB所对的劣弧为圆的,圆的半径为2cm,求AB的长.6.如图4,∠AOB=90°,C、D是AB三等分点,AB分别交OC、OD于点E、F,求证:AE=BF=CD.【作业】A组1. 下列说法正确的是( )A.相等的圆心角所对的弧相等 B.在同圆中,等弧所对的圆心角相等C.弦相等,则圆心到弦的距离相等 D.圆心到弦的距离相等,则弦相等2. 如图,圆心角∠AOB=25°,将旋转n°得到,则∠COD的度数为( )A.25° B.25°+n° C.50° D.50°+n° 第2题 第3题 第4题3. 如图,在⊙O中,AB,CD是两条弦,OM⊥CD于点M,ON⊥AB于点N.若AB=CD,则下列结论不正确的是( )A.∠AON=∠DOM B.AN=DM C.OM=DM D.OM=ON4. 如图,点A、B、C、D在⊙O上,且AB=BC=CD.若∠AOB=80°,则∠AOD的度数为________.5. 如图,点A,B,C,D在⊙O上,AB=CD,AC与BD相等吗?为什么? 第5题B组6. ⊙O中,M为的中点,则下列结论正确的是( )A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定7. 如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为________.8. 如图,在⊙O中,=,∠ACB=60°.(1) 求证:∠AOB=∠BOC=∠AOC;(2) 若D是的中点,求证:四边形OADB是菱形. 第8题
PAGE
第6/6页
【感悟】1. 是圆心角;2.圆不仅是 对称图形,而且是 对称图形,对称中心是 .3.弧、弦、圆心角之间的关系定理: .在关系定理中,为什么要说“同圆或等圆”?能不能去掉?在证明圆中弧、弦、圆心角相等时,可以通过证明本量中以外的量相等的来实现. 【补充思考】
【检测】1.如果两个圆心角相等,那么( )A.这两个圆心角所对的弦相等; B.这两个圆心角所对的弧相等;C.这两个圆心角所对的弦的弦心距(圆心到弦的距离)相等; D.以上说法都不对2.如图1,⊙O中,如果=2,那么( ).A.AB=2AC B.AB=AC C.AB<2AC D.AB>2AC 图1 图2 图3 图43.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.4.已知:如图2,已知AB和CD是⊙O的两条直径,弦CE∥AB,求证: = 5.如图3,在⊙O中,弦AB所对的劣弧为圆的,圆的半径为2cm,求AB的长.6.如图4,∠AOB=90°,C、D是AB三等分点,AB分别交OC、OD于点E、F,求证:AE=BF=CD.【作业】A组1. 下列说法正确的是( )A.相等的圆心角所对的弧相等 B.在同圆中,等弧所对的圆心角相等C.弦相等,则圆心到弦的距离相等 D.圆心到弦的距离相等,则弦相等2. 如图,圆心角∠AOB=25°,将旋转n°得到,则∠COD的度数为( )A.25° B.25°+n° C.50° D.50°+n° 第2题 第3题 第4题3. 如图,在⊙O中,AB,CD是两条弦,OM⊥CD于点M,ON⊥AB于点N.若AB=CD,则下列结论不正确的是( )A.∠AON=∠DOM B.AN=DM C.OM=DM D.OM=ON4. 如图,点A、B、C、D在⊙O上,且AB=BC=CD.若∠AOB=80°,则∠AOD的度数为________.5. 如图,点A,B,C,D在⊙O上,AB=CD,AC与BD相等吗?为什么? 第5题B组6. ⊙O中,M为的中点,则下列结论正确的是( )A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定7. 如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为________.8. 如图,在⊙O中,=,∠ACB=60°.(1) 求证:∠AOB=∠BOC=∠AOC;(2) 若D是的中点,求证:四边形OADB是菱形. 第8题
PAGE
第6/6页
同课章节目录
