24.1.4圆周角 第1课时同步导学案(无答案)
文档属性
| 名称 | 24.1.4圆周角 第1课时同步导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览

文档简介
学习课题:《24.1.4圆周角(1)》学习目标:1.知道圆周角的概念,能够识别圆周角;2.知道圆周角定理及其推论.并会熟练运用它们解决问题.3.经历圆周角定理的证明,学会分情况证明命题的思想和方法,体会类比、分类的数学方法.重点知识:圆周角定理及其推论的应用.难点问题:定理的灵活应用以及辅助线的添加.学习策略指导:与圆心角一样,圆周角也是研究圆时重点研究的一类角,圆周角定理揭示了一条弧所对的圆周角与圆心角之间的数量关系,从而把圆周角与相对应的弧、弦联系起来.圆周角定理及其推论为与圆有关的角、线段的计算、证明提供了十分便捷的方法和思路.圆周角定理的证明,采用归纳法,通过分类讨论,把一般问题转化为特殊情况来证明,渗透了分类讨论和化一般为特殊的划归思想. 【补充思考】
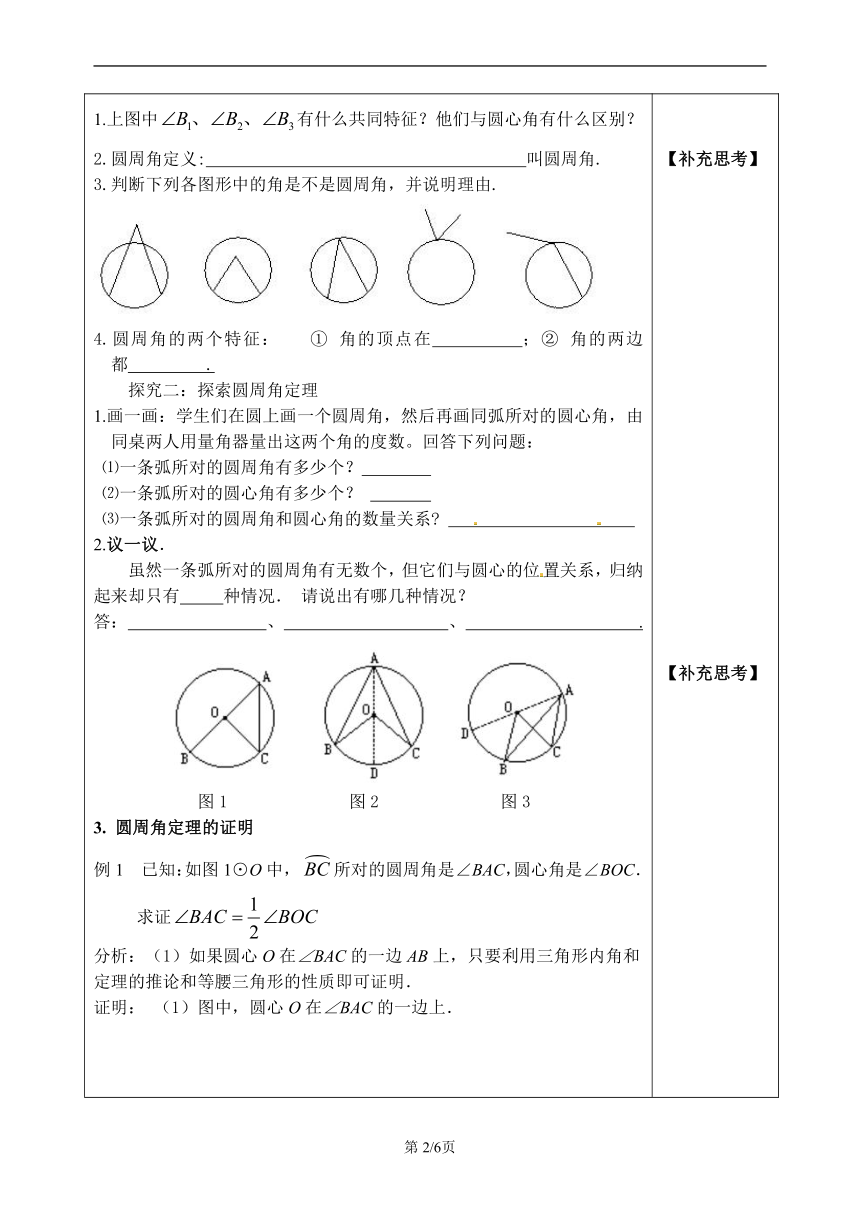
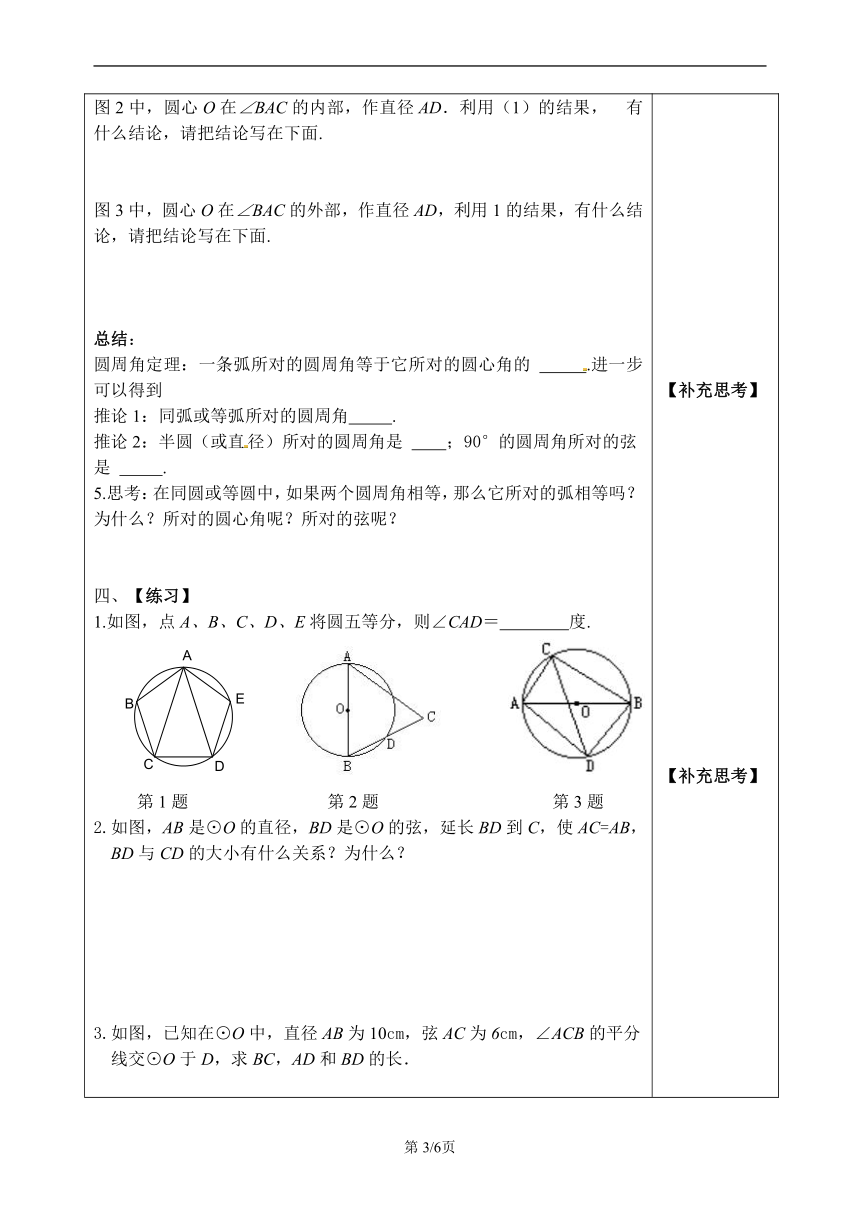
【回顾】1.什么叫圆心角?请画图说明.2.画图举例说明圆心角、弦、弧之间有什么内在联系?【导入】如图,点A在⊙O外,点在⊙O上,点C在⊙O内,度量的大小,你有什么发现?【探究】探究一:圆周角定义1.上图中有什么共同特征?他们与圆心角有什么区别?2.圆周角定义: 叫圆周角.3.判断下列各图形中的角是不是圆周角,并说明理由.4.圆周角的两个特征: ① 角的顶点在 ;② 角的两边都 .探究二:探索圆周角定理1.画一画:学生们在圆上画一个圆周角,然后再画同弧所对的圆心角,由同桌两人用量角器量出这两个角的度数。回答下列问题:⑴一条弧所对的圆周角有多少个? ⑵一条弧所对的圆心角有多少个? ⑶一条弧所对的圆周角和圆心角的数量关系 2.议一议.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置关系,归纳起来却只有 种情况. 请说出有哪几种情况? 答: 、 、 . 图1 图2 图33. 圆周角定理的证明例1 已知:如图1⊙O中, 所对的圆周角是∠BAC,圆心角是∠BOC.求证分析:(1)如果圆心O在∠BAC的一边AB上,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明.证明: (1)图中,圆心O在∠BAC的一边上.图2中,圆心O在∠BAC的内部,作直径AD.利用(1)的结果, 有什么结论,请把结论写在下面.图3中,圆心O在∠BAC的外部,作直径AD,利用1的结果,有什么结论,请把结论写在下面.总结:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的 .进一步可以得到推论1:同弧或等弧所对的圆周角 .推论2:半圆(或直径)所对的圆周角是 ;90°的圆周角所对的弦是 .5.思考:在同圆或等圆中,如果两个圆周角相等,那么它所对的弧相等吗?为什么?所对的圆心角呢?所对的弦呢?四、【练习】1.如图,点A、B、C、D、E将圆五等分,则∠CAD= 度.第1题 第2题 第3题2.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?3.如图,已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长. 【补充思考】【补充思考】【补充思考】【补充思考】【补充思考】【补充思考】
【感悟】一个定义:一个定理及两个推论:一种方法:一种思想: 【补充思考】
【检测】1.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )A.15 B.28 C.29 D.342.如图2,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( ) A.100° B.80° C.70° D.50°3.如图3,在⊙O中,弦BE与CD相交于点F,CB、ED的延长线交于点A,如果∠A=30°, ∠CFE=70°,∠CDE=( ) A.20° B.40 ° C.50 ° D.60°4.如图4,△ABC的三个顶点都在⊙O上,AD、BE是高,交点为H,BE的延长线交⊙O于F,下列结论:①∠BAO=∠CAD;②AO=AH;③DH=DC;④EH=EF,其中正确的的结论( )A.①② B. ②③ C. ①④ D. ③④5.如图,OA=OB=OC都是⊙O的半径,∠AOB=2∠BOC,求证:∠ACB=2∠BAC.6.如右图,在⊙O中,∠ACB=∠BDC=60°,AC=cm,(1)求∠ABC的度数; (2)求⊙O的面积【作业】A组1. 如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )A.∠B B.∠C C.∠DEB D.∠D 第1题 第2题 第3题2.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则∠BOC的度数为( )A.30° B.40° C.50° D.60°3.如图,BC是⊙O的直径,A,D是⊙O上的两点,连接AB,AD,BD,若∠ADB=70°,则∠ABC的度数是( )A.20° B.70° C.30° D.90°4. 如图,C、D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD= .5. 如图,点A,B,C在⊙O上,∠ACB=90°,∠ACB的平分线交⊙O于点D,连接AB,BD.若AC=6,BD=5,求BC的长. 第5题B组6. 如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )A.70° B.55° C.45° D.35° 第6题 第7题7. 如图所示,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,CD=,则⊙O的半径是 .8. 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且点D为的中点.若∠A=70°,求∠DBE的度数; 第8题
PAGE
第6/6页
【回顾】1.什么叫圆心角?请画图说明.2.画图举例说明圆心角、弦、弧之间有什么内在联系?【导入】如图,点A在⊙O外,点在⊙O上,点C在⊙O内,度量的大小,你有什么发现?【探究】探究一:圆周角定义1.上图中有什么共同特征?他们与圆心角有什么区别?2.圆周角定义: 叫圆周角.3.判断下列各图形中的角是不是圆周角,并说明理由.4.圆周角的两个特征: ① 角的顶点在 ;② 角的两边都 .探究二:探索圆周角定理1.画一画:学生们在圆上画一个圆周角,然后再画同弧所对的圆心角,由同桌两人用量角器量出这两个角的度数。回答下列问题:⑴一条弧所对的圆周角有多少个? ⑵一条弧所对的圆心角有多少个? ⑶一条弧所对的圆周角和圆心角的数量关系 2.议一议.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置关系,归纳起来却只有 种情况. 请说出有哪几种情况? 答: 、 、 . 图1 图2 图33. 圆周角定理的证明例1 已知:如图1⊙O中, 所对的圆周角是∠BAC,圆心角是∠BOC.求证分析:(1)如果圆心O在∠BAC的一边AB上,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明.证明: (1)图中,圆心O在∠BAC的一边上.图2中,圆心O在∠BAC的内部,作直径AD.利用(1)的结果, 有什么结论,请把结论写在下面.图3中,圆心O在∠BAC的外部,作直径AD,利用1的结果,有什么结论,请把结论写在下面.总结:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的 .进一步可以得到推论1:同弧或等弧所对的圆周角 .推论2:半圆(或直径)所对的圆周角是 ;90°的圆周角所对的弦是 .5.思考:在同圆或等圆中,如果两个圆周角相等,那么它所对的弧相等吗?为什么?所对的圆心角呢?所对的弦呢?四、【练习】1.如图,点A、B、C、D、E将圆五等分,则∠CAD= 度.第1题 第2题 第3题2.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?3.如图,已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长. 【补充思考】【补充思考】【补充思考】【补充思考】【补充思考】【补充思考】
【感悟】一个定义:一个定理及两个推论:一种方法:一种思想: 【补充思考】
【检测】1.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )A.15 B.28 C.29 D.342.如图2,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( ) A.100° B.80° C.70° D.50°3.如图3,在⊙O中,弦BE与CD相交于点F,CB、ED的延长线交于点A,如果∠A=30°, ∠CFE=70°,∠CDE=( ) A.20° B.40 ° C.50 ° D.60°4.如图4,△ABC的三个顶点都在⊙O上,AD、BE是高,交点为H,BE的延长线交⊙O于F,下列结论:①∠BAO=∠CAD;②AO=AH;③DH=DC;④EH=EF,其中正确的的结论( )A.①② B. ②③ C. ①④ D. ③④5.如图,OA=OB=OC都是⊙O的半径,∠AOB=2∠BOC,求证:∠ACB=2∠BAC.6.如右图,在⊙O中,∠ACB=∠BDC=60°,AC=cm,(1)求∠ABC的度数; (2)求⊙O的面积【作业】A组1. 如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )A.∠B B.∠C C.∠DEB D.∠D 第1题 第2题 第3题2.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则∠BOC的度数为( )A.30° B.40° C.50° D.60°3.如图,BC是⊙O的直径,A,D是⊙O上的两点,连接AB,AD,BD,若∠ADB=70°,则∠ABC的度数是( )A.20° B.70° C.30° D.90°4. 如图,C、D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD= .5. 如图,点A,B,C在⊙O上,∠ACB=90°,∠ACB的平分线交⊙O于点D,连接AB,BD.若AC=6,BD=5,求BC的长. 第5题B组6. 如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )A.70° B.55° C.45° D.35° 第6题 第7题7. 如图所示,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,CD=,则⊙O的半径是 .8. 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且点D为的中点.若∠A=70°,求∠DBE的度数; 第8题
PAGE
第6/6页
同课章节目录
