24.1.4圆周角 第2课时同步导学案(无答案)
文档属性
| 名称 | 24.1.4圆周角 第2课时同步导学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 232.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览


文档简介
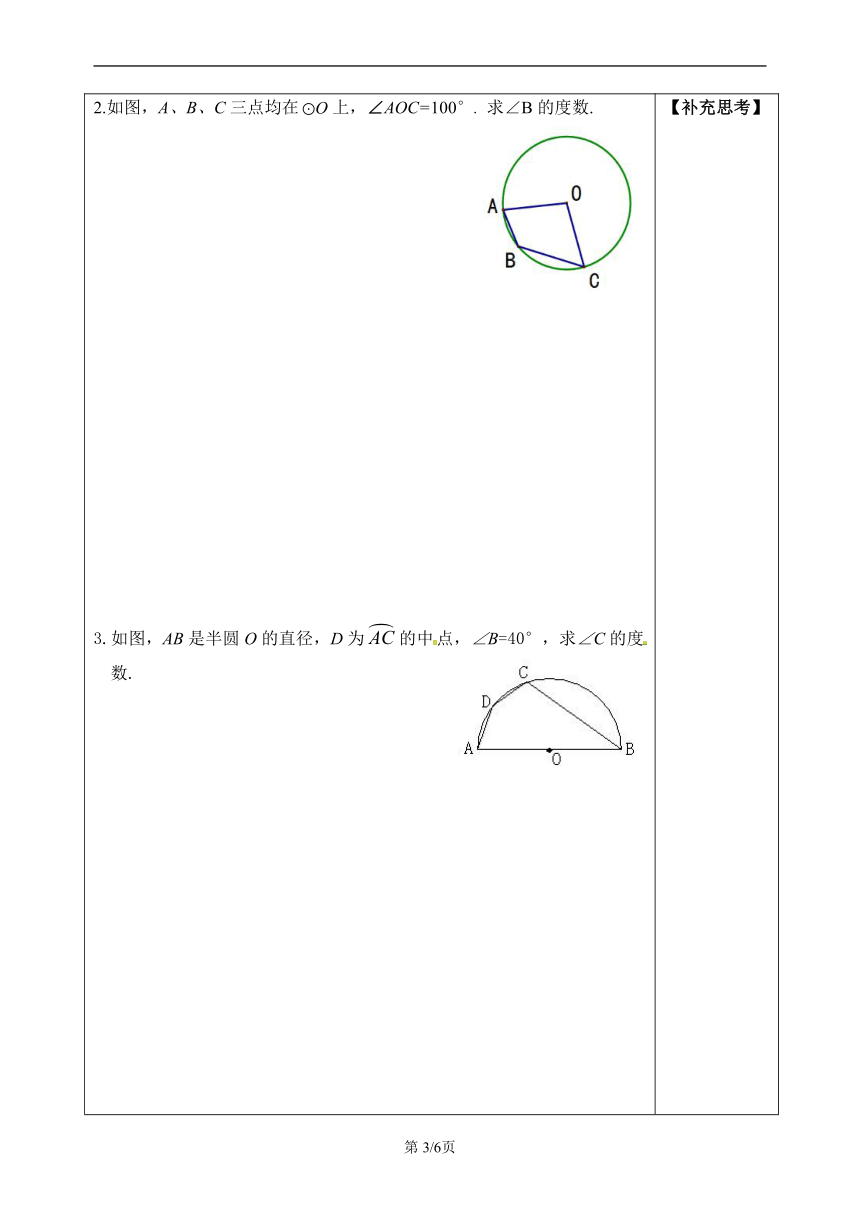
学习课题:《24.1.4圆周角(2)》学习目标:1.能结合图形说明什么是圆内接多边形和多边形的外接圆;2.知道圆内接四边形的性质,并且能利用圆内接四边形的性质解决相关问题.重点知识:圆内接四边形和它的性质及圆周角定理及其推论的进一步运用.难点问题:运用圆内接四边形的性质解决相关问题.学习策略指导:圆内接四边形的四个角都是圆周角,利用圆周角定理,可以把圆内接四边形的四个内角和相应的圆心角联系起来,得到圆内接四边形的性质.圆内接四边形的性质在圆中探索角相等或互补关系时经常用到,要注意掌握. 【补充思考】
【回顾】1.如图,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD= .2.如图,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON= .3.如图,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M.若∠BAC=60°,∠ABC=50°,则∠CBM= ,∠AMB= .4.⊙O中,若弦AB长2cm,O到AB的距离为cm,则此弦所对的圆周角等于 . 【补充思考】
【导入】这节我们学习有关圆内接四边形的知识,同时对圆周角定理的灵活应用,做进一步的训练.【探究】活动一:自学课本87页,完成下列题目.若一个多边形各顶点都在 ,那么,这个多边形叫做 ,这个圆叫做这个多边形的 .如右图,四边形ABCD为⊙O的 ;⊙O为四边形ABCD的 .活动二:圆内接四边形的性质1.如上图,圆内接四边形的内角间有哪些关系呢?用量角器量一量,并作猜想.⑴和之间是什么关系?答: .⑵和之间是什么关系?答: .我们发现:圆内接四边形 .2.证明猜想:已知:四边形ABCD是⊙O的内接四边形.求证:,分析:圆内接四边形的四个内角均为圆周角,我们可以利用圆周角定理及其推论,探索它们之间的关系.证明:【练习】1.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若,求∠DCE的度数. 【补充思考】
2.如图,A、B、C三点均在上,∠AOC=100°. 求∠B的度数.3.如图,AB是半圆O的直径,D为的中点,∠B=40°,求∠C的度 数. 【补充思考】
【感悟】1.什么是圆内接四边形?圆内接四边形的性质是什么?2.在应用圆周角定理或圆内接四边形的性质解决有关问题的过程中常用的做辅助线的方法是什么? 3.到现在为止你证明角相等或互补的方法有哪些?证明线段相等的方法呢? 【补充思考】
【检测】1.在圆内接四边形ABCD中,∶∶∶可以是( )A.1∶2∶3∶4 B. 1∶3∶2∶4 C. 4∶2∶3∶1 D.4∶2∶1∶32.若圆内接四边形相邻三个外角的度数的比是2∶4∶3,则该四边形内角中最大的角是____度.3.如图AB是⊙O的直径,C,D,E是⊙O上的点,求∠ACE+∠EDB的度数.4.如图,AB为⊙O的直径,点CD在⊙O上,若∠AOD=,求∠BCD的度数.5.如图,在△ABC中,AB=AC,BD是∠ABC的角平分线,△ABD的外接圆交BC于E.求证:AD=EC.【作业】A组1. 如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )A.110° B.120° C.135° D.140° 第1题 第2题 第3题 第4题 2.如图,四边形ABCD是半圆的内接四边形,AB是直径,=.若∠C=110°,则∠ABC的度数等于( )A.55° B.60° C.65° D.70°3.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是上的点.若∠BOC=40°,则∠D的度数为( )A.100° B.110° C.120° D.130°4. 如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD.若∠C=70°,则∠ADE的度数为________.5. 如图,四边形ABED是圆的内接四边形,延长AD、BE相交于点C,已知∠C=∠EDC.(1)求证:AB=AC;(2)若AB是四边形ABED外接圆的直径,求证:=. 第5题B组6. 如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是( )A.130° B.140° C.150° D.160° 第6题 第7题7. 如图,在平面直角坐标系中,O为坐标原点,以点O为圆心作⊙O,点A,C分别是⊙O与x轴负半轴、y轴正半轴的交点,点B,D在⊙O上,连接AB,BC,CD,DA,那么∠ADC的度数是________.8. 已知四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,∠BCA=60°,∠BAC=30°,求∠BDC的大小. 第8题
PAGE
第6/6页
【回顾】1.如图,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD= .2.如图,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON= .3.如图,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M.若∠BAC=60°,∠ABC=50°,则∠CBM= ,∠AMB= .4.⊙O中,若弦AB长2cm,O到AB的距离为cm,则此弦所对的圆周角等于 . 【补充思考】
【导入】这节我们学习有关圆内接四边形的知识,同时对圆周角定理的灵活应用,做进一步的训练.【探究】活动一:自学课本87页,完成下列题目.若一个多边形各顶点都在 ,那么,这个多边形叫做 ,这个圆叫做这个多边形的 .如右图,四边形ABCD为⊙O的 ;⊙O为四边形ABCD的 .活动二:圆内接四边形的性质1.如上图,圆内接四边形的内角间有哪些关系呢?用量角器量一量,并作猜想.⑴和之间是什么关系?答: .⑵和之间是什么关系?答: .我们发现:圆内接四边形 .2.证明猜想:已知:四边形ABCD是⊙O的内接四边形.求证:,分析:圆内接四边形的四个内角均为圆周角,我们可以利用圆周角定理及其推论,探索它们之间的关系.证明:【练习】1.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若,求∠DCE的度数. 【补充思考】
2.如图,A、B、C三点均在上,∠AOC=100°. 求∠B的度数.3.如图,AB是半圆O的直径,D为的中点,∠B=40°,求∠C的度 数. 【补充思考】
【感悟】1.什么是圆内接四边形?圆内接四边形的性质是什么?2.在应用圆周角定理或圆内接四边形的性质解决有关问题的过程中常用的做辅助线的方法是什么? 3.到现在为止你证明角相等或互补的方法有哪些?证明线段相等的方法呢? 【补充思考】
【检测】1.在圆内接四边形ABCD中,∶∶∶可以是( )A.1∶2∶3∶4 B. 1∶3∶2∶4 C. 4∶2∶3∶1 D.4∶2∶1∶32.若圆内接四边形相邻三个外角的度数的比是2∶4∶3,则该四边形内角中最大的角是____度.3.如图AB是⊙O的直径,C,D,E是⊙O上的点,求∠ACE+∠EDB的度数.4.如图,AB为⊙O的直径,点CD在⊙O上,若∠AOD=,求∠BCD的度数.5.如图,在△ABC中,AB=AC,BD是∠ABC的角平分线,△ABD的外接圆交BC于E.求证:AD=EC.【作业】A组1. 如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )A.110° B.120° C.135° D.140° 第1题 第2题 第3题 第4题 2.如图,四边形ABCD是半圆的内接四边形,AB是直径,=.若∠C=110°,则∠ABC的度数等于( )A.55° B.60° C.65° D.70°3.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是上的点.若∠BOC=40°,则∠D的度数为( )A.100° B.110° C.120° D.130°4. 如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD.若∠C=70°,则∠ADE的度数为________.5. 如图,四边形ABED是圆的内接四边形,延长AD、BE相交于点C,已知∠C=∠EDC.(1)求证:AB=AC;(2)若AB是四边形ABED外接圆的直径,求证:=. 第5题B组6. 如图,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是( )A.130° B.140° C.150° D.160° 第6题 第7题7. 如图,在平面直角坐标系中,O为坐标原点,以点O为圆心作⊙O,点A,C分别是⊙O与x轴负半轴、y轴正半轴的交点,点B,D在⊙O上,连接AB,BC,CD,DA,那么∠ADC的度数是________.8. 已知四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,∠BCA=60°,∠BAC=30°,求∠BDC的大小. 第8题
PAGE
第6/6页
同课章节目录
