24.2.2直线与圆的位置关系 第2课时同步导学案(无答案)
文档属性
| 名称 | 24.2.2直线与圆的位置关系 第2课时同步导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览

文档简介
学习课题:《24.2.2 直线和圆的位置关系(2)》学习目标:1.记住并理解切线的判定定理和切线的性质定理,并能初步运用它解决简单的问题.2.知道判定切线的三种常用方法,并能选择合适的方法来判定. 能够正确区分和运用切线的判定定理和切线的性质定理.3.掌握在解决切线的问题中常用的辅助线的作法.重点知识: 记住并掌握切线的判定定理和性质定理.难点问题: 能熟练运用切线的判定定理和性质定理解决有关问题.学习策略指导:认真通读教材,对于切线的判定定理,首先要分清定理的条件和结论,运用时“经过半径的外端”和“垂直于这条半径”两个条件缺一不可;了解切线性质定理的的证明(用反证法)对于学生不做要求; 在运用切线的判定定理和性质定理进行证明时,关注辅助线的添加方法,一半分为两种情况:当已知点在圆上时,连半径证垂直;当未知点在圆上时,作出垂直时证半径。 【补充思考】
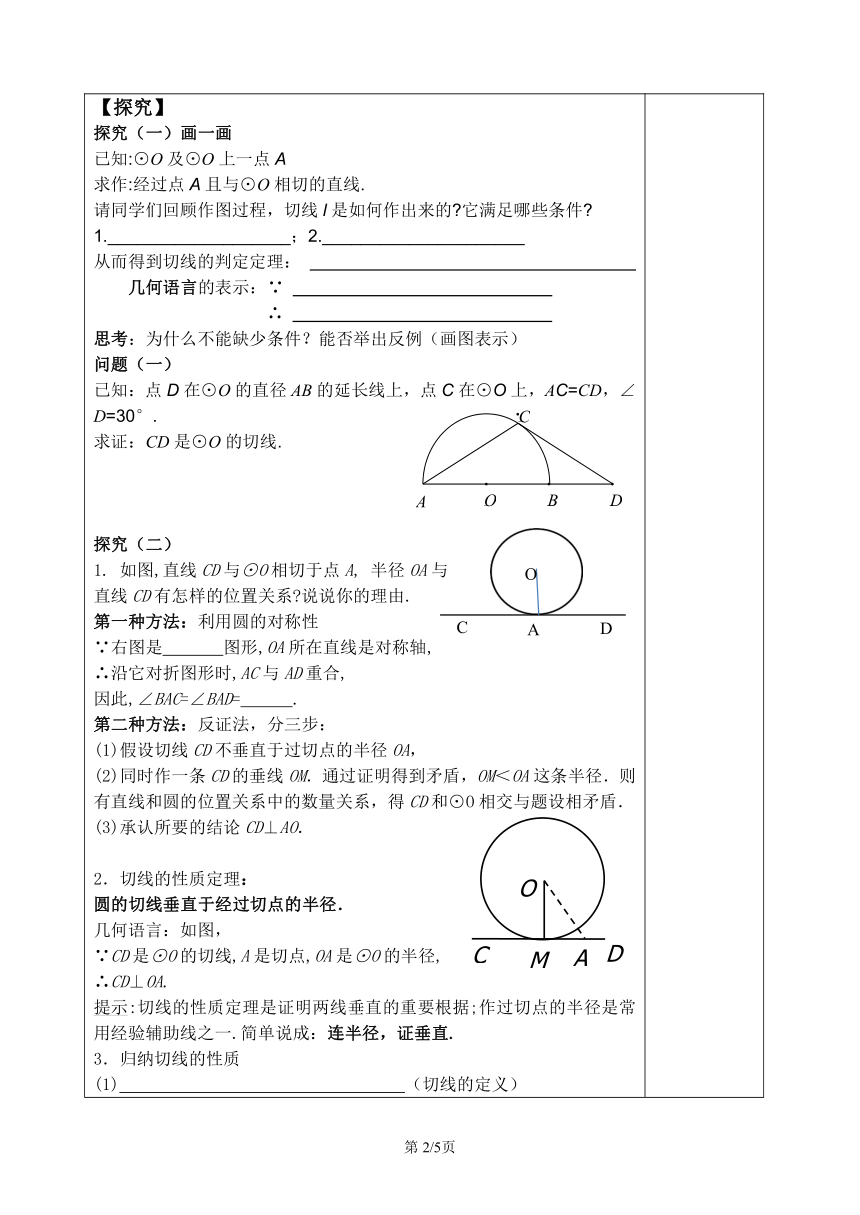
【回顾】 问题:直线和圆有几种位置关系?如何判断直线与圆相切?有几种方法?判断的方法:1. 2. 【导入】如图,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?思考: 我们常遇到判定直线和圆相切的情况,如果我们始终用寻找公共点的个数和圆心到直线的距离来判断很不方便,也难于操作,还有没有其它的方法呢?【探究】探究(一)画一画已知:⊙O及⊙O上一点A求作:经过点A且与⊙O相切的直线.请同学们回顾作图过程,切线l是如何作出来的 它满足哪些条件 1.___________________;2._____________________从而得到切线的判定定理: 几何语言的表示:∵ ∴ 思考:为什么不能缺少条件?能否举出反例(画图表示)问题(一) 已知:点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°. 求证:CD是⊙O的切线. 探究(二)如图,直线CD与⊙O相切于点A, 半径OA与直线CD有怎样的位置关系 说说你的理由.第一种方法:利用圆的对称性∵右图是 图形,OA所在直线是对称轴,∴沿它对折图形时,AC与AD重合,因此,∠BAC=∠BAD= .第二种方法:反证法,分三步:(1)假设切线CD不垂直于过切点的半径OA,(2)同时作一条CD的垂线OM.通过证明得到矛盾,OM<OA这条半径.则有直线和圆的位置关系中的数量关系,得CD和⊙O相交与题设相矛盾.(3)承认所要的结论CD⊥AO.2.切线的性质定理:圆的切线垂直于经过切点的半径.几何语言:如图,∵CD是⊙O的切线,A是切点,OA是⊙O的半径,∴CD⊥OA.提示:切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.简单说成:连半径,证垂直.3.归纳切线的性质(1) (切线的定义)(2) (判定方法<2>的逆命题)(3) (切线的性质定理)问题(二)已知:如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D. 求证:AC平分∠DAB.【练习】如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )A. 70° B. 35° C. 20° D. 10°2.如图,在△ABC中,AB=AC,∠BAC=120°,⊙A与BC相切于点D,与AB相交于点E,则∠BDE等于___度.3. 如图,DB是⊙O的直径,点A在BD的延长线上AB=OB,∠CAD=30°.求证:AC是⊙O的切线. 【感悟】1.判定一条直线是圆的切线的三种方法.(1)定义(2)数量关系(3)判定定理 (注意两个条件缺一不可) 2.切线的性质定理和判定定理:3.辅助线作法:(1)公共点确定: (2)公共点不确定: 【检测】1.判断下列命题是否正确. (1)经过半径外端的直线是圆的切线.( )(2)垂直于半径的直线是圆的切线.( ) (3)过半径的端点并且垂直于这半径的直线是圆的切线.( )(4)以等腰三角形的顶点为圆心,底边上的中线为半径的圆与底边相切( )如图,AB是⊙O的弦,过点A作⊙O的切线AC,如果∠BAC=55°,则∠AOB的度数是( )A. 55° B. 90° C. 110° D. 120°如图,AB是⊙O的直径,P为AB延长线上的一点,PC切⊙O于点C,若PB=2,AB=6,求PC的长.4.如图,AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT是⊙O的切线. 【补充思考】
【作业】A组1.如图,为的切线,点为切点,的延长线交于点,若,则的度数是 A. B. C. D. 第1题 第2题 第3题2.如图,点、是上两点,连接并延长交切线于点,连接、、、,若,则的度数为 A. B. C. D.3.在中,,,与相切于点,若,则的长为 A. B. C.3 D.4.已知在矩形中,,对角线.的半径长为12,下列说法正确的是 A.与直线相交 B.与直线相切 C.点在上 D.点在内B组5.如图, 以O为圆心的两个同心圆中, 大圆的弦AB是小圆的切线, 点P为切点 .若大圆半径为 2 ,小圆半径为 1 ,则AB的长为 A . B . C . D . 2 第5题 第6题6.如图,是直径,是切线,交与点.(1)若点在上,连接,且,求证:是的切线;(2)若.,求的度数
O
A
A
_
B
_
D
_
O
_
C
O
A
C
D
C
D
A
M
O
A
D
O
B
C
O
T
B
A
PAGE
第5/5页
【回顾】 问题:直线和圆有几种位置关系?如何判断直线与圆相切?有几种方法?判断的方法:1. 2. 【导入】如图,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?思考: 我们常遇到判定直线和圆相切的情况,如果我们始终用寻找公共点的个数和圆心到直线的距离来判断很不方便,也难于操作,还有没有其它的方法呢?【探究】探究(一)画一画已知:⊙O及⊙O上一点A求作:经过点A且与⊙O相切的直线.请同学们回顾作图过程,切线l是如何作出来的 它满足哪些条件 1.___________________;2._____________________从而得到切线的判定定理: 几何语言的表示:∵ ∴ 思考:为什么不能缺少条件?能否举出反例(画图表示)问题(一) 已知:点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°. 求证:CD是⊙O的切线. 探究(二)如图,直线CD与⊙O相切于点A, 半径OA与直线CD有怎样的位置关系 说说你的理由.第一种方法:利用圆的对称性∵右图是 图形,OA所在直线是对称轴,∴沿它对折图形时,AC与AD重合,因此,∠BAC=∠BAD= .第二种方法:反证法,分三步:(1)假设切线CD不垂直于过切点的半径OA,(2)同时作一条CD的垂线OM.通过证明得到矛盾,OM<OA这条半径.则有直线和圆的位置关系中的数量关系,得CD和⊙O相交与题设相矛盾.(3)承认所要的结论CD⊥AO.2.切线的性质定理:圆的切线垂直于经过切点的半径.几何语言:如图,∵CD是⊙O的切线,A是切点,OA是⊙O的半径,∴CD⊥OA.提示:切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.简单说成:连半径,证垂直.3.归纳切线的性质(1) (切线的定义)(2) (判定方法<2>的逆命题)(3) (切线的性质定理)问题(二)已知:如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D. 求证:AC平分∠DAB.【练习】如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )A. 70° B. 35° C. 20° D. 10°2.如图,在△ABC中,AB=AC,∠BAC=120°,⊙A与BC相切于点D,与AB相交于点E,则∠BDE等于___度.3. 如图,DB是⊙O的直径,点A在BD的延长线上AB=OB,∠CAD=30°.求证:AC是⊙O的切线. 【感悟】1.判定一条直线是圆的切线的三种方法.(1)定义(2)数量关系(3)判定定理 (注意两个条件缺一不可) 2.切线的性质定理和判定定理:3.辅助线作法:(1)公共点确定: (2)公共点不确定: 【检测】1.判断下列命题是否正确. (1)经过半径外端的直线是圆的切线.( )(2)垂直于半径的直线是圆的切线.( ) (3)过半径的端点并且垂直于这半径的直线是圆的切线.( )(4)以等腰三角形的顶点为圆心,底边上的中线为半径的圆与底边相切( )如图,AB是⊙O的弦,过点A作⊙O的切线AC,如果∠BAC=55°,则∠AOB的度数是( )A. 55° B. 90° C. 110° D. 120°如图,AB是⊙O的直径,P为AB延长线上的一点,PC切⊙O于点C,若PB=2,AB=6,求PC的长.4.如图,AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT是⊙O的切线. 【补充思考】
【作业】A组1.如图,为的切线,点为切点,的延长线交于点,若,则的度数是 A. B. C. D. 第1题 第2题 第3题2.如图,点、是上两点,连接并延长交切线于点,连接、、、,若,则的度数为 A. B. C. D.3.在中,,,与相切于点,若,则的长为 A. B. C.3 D.4.已知在矩形中,,对角线.的半径长为12,下列说法正确的是 A.与直线相交 B.与直线相切 C.点在上 D.点在内B组5.如图, 以O为圆心的两个同心圆中, 大圆的弦AB是小圆的切线, 点P为切点 .若大圆半径为 2 ,小圆半径为 1 ,则AB的长为 A . B . C . D . 2 第5题 第6题6.如图,是直径,是切线,交与点.(1)若点在上,连接,且,求证:是的切线;(2)若.,求的度数
O
A
A
_
B
_
D
_
O
_
C
O
A
C
D
C
D
A
M
O
A
D
O
B
C
O
T
B
A
PAGE
第5/5页
同课章节目录
