24.2.2直线与圆的位置关系 第3课时同步导学案(无答案)
文档属性
| 名称 | 24.2.2直线与圆的位置关系 第3课时同步导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览

文档简介
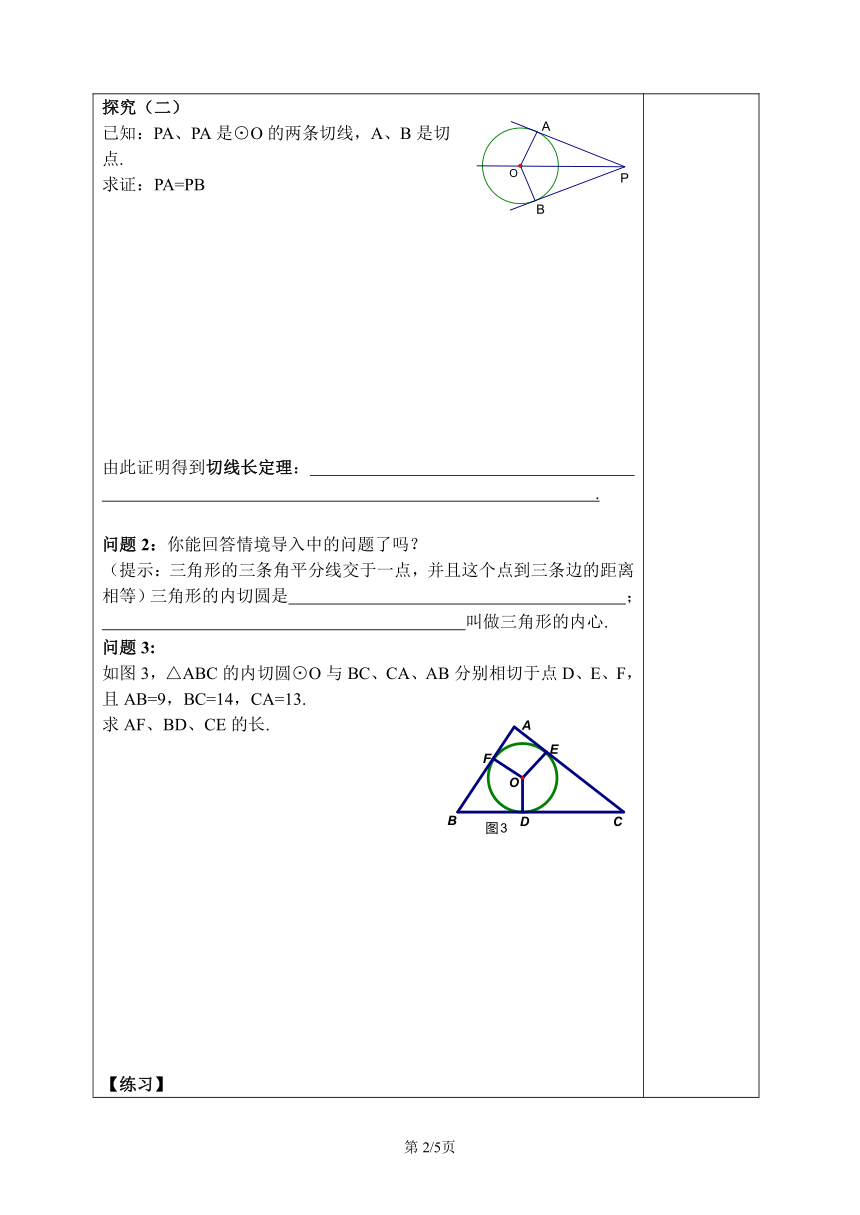
学习课题:《24.2.2 直线和圆的位置关系(3) 》学习目标:1.知道切线长的定义,能说出并掌握切线长定理,初步学会运用切线长定理进行计算与证明;2.知道并记住三角形的内切圆和三角形的内心的概念;3.学会利用方程思想解决几何问题,体验数形结合思想.重点知识:切线长定理及应用难点问题:切线长定理的应用学习策略指导:学习之前要首先复习切线的性质和判定,关注全等三角形的构造与证明在本节课的学习中的作用.在探究过程中关注圆的轴对称性,利用圆的对称性,进一步理解切线长定理,在基本图形中注意结论的多样性图形的多变性.在做题的同事注意总结证明方法的灵活运用.【回顾】1.切线的判定定理和性质定理?2.切线的判定方法有哪些?3.证明切线时常用的辅助线做法? 【导入】如图2是一块三角形铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?【探究】探究(一)在纸上画一⊙O,PA为⊙O的一条切线,沿着直线PO将纸对折,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的切线吗?利用图形的轴对称性,说明图1中的PA与PB,∠APO与∠APO有什么关系?问题:1:切线长是指 .思考:切线长与切线有什么区别与联系?探究(二)已知:PA、PA是⊙O的两条切线,A、B是切点.求证:PA=PB 由此证明得到切线长定理: .问题2:你能回答情境导入中的问题了吗?(提示:三角形的三条角平分线交于一点,并且这个点到三条边的距离相等)三角形的内切圆是 ; 叫做三角形的内心.问题3:如图3,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13.求AF、BD、CE的长.【练习】1.如图,Rt△ABC中,∠C=90°,AB、BC、CA的长分别为c、a、b.求△ABC的内切圆半径r. 2.如图3,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=3,BF=2,且△ABC的面积为6.求内切圆的半径r.【感悟】1.切线长定理.2.三角形的内切圆、内心、外接圆、外心的概念.3.直角三角形内切圆半径r=.【检测】1.下列说法正确的是( )A.垂直于半径的直线是圆的切线 B.经过三点一定可以作圆C.圆的切线垂直于圆的半径 D.每个三角形都有一个内切圆2.如图,⊙O内切于,切点分别为.已知,,连结,那么等于( )A. B. C. D.3.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________4.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为 5.为了测量一个圆铁环的半径,某同学用了如下方法,将铁环平放在一个平桌面上,用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据,进而求出铁环半径,若测得PA=5cm,求铁环的半径. 【补充思考】
D
O
A
F
C
B
E
A
P
60°
30°
PAGE
第5/5页
D
O
A
F
C
B
E
A
P
60°
30°
PAGE
第5/5页
同课章节目录
