24.3 正多边形和圆 第1课时同步导学案(无答案)
文档属性
| 名称 | 24.3 正多边形和圆 第1课时同步导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 624.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览

文档简介
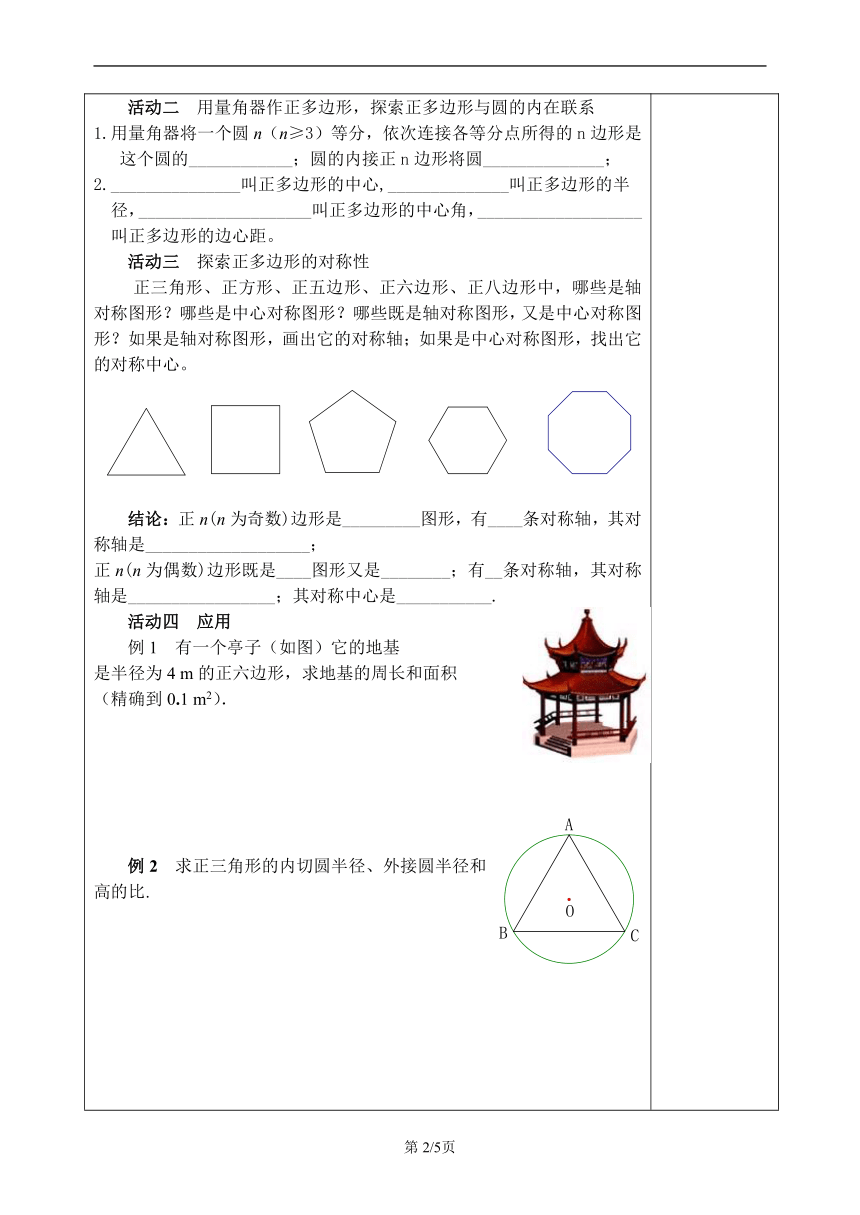
学习课题:《24.3正多边形和圆(1)》学习目标:1.通过自己观察、思考,知道正多边形与圆的关系;知道正多边形的中心、半径、边心距、中心角等概念.2.在经历探索正多边形与圆的关系过程中,能运用圆的有关知识解决问题,并能运用正多边形的知识解决圆的有关计算问题.重点知识:探索正多边形与圆的关系,正多边形的概念,并进行有关计算. 难点问题:学会构造直角三角形进行有关计算.学习策略指导:细读教材,感受正多边形和圆的关系,对比圆的概念结合圆与正多边形的关系理解正多边形的有关概念,借助解直角三角形的知识进行正多边形的计算. 【补充思考】
【回顾】①么叫正多边形?矩形是正多边形吗?菱形呢?正方形呢? ②从你身边举出两三个正多边形的实例,正多边形是轴对称图形吗?是中心对称图形吗?如果是,对称中心在哪里?【导入】数学源于生活,让我们观看下列美丽的图案,感受数学之美.问题1 这些美丽的图案,都是在日常生活中我们经常能看到的、利用正多边形设计的物体.你能从这些图案中找出正多边形来吗? 问题2 你知道正多边形和圆有什么关系吗? 【探究】活动一 观察生活中的一些图形,归纳它们的共同特征,引入正多边形的概念_________________________的多边形叫做正多边形。思考:各边相等的多边形一定是正多边形吗?各角相等的多边形呢?若不是举例说明.总结:各边相等与各角相等必须同时成立的多边形才是正多边形. 活动二 用量角器作正多边形,探索正多边形与圆的内在联系1.用量角器将一个圆n(n≥3)等分,依次连接各等分点所得的n边形是这个圆的____________;圆的内接正n边形将圆______________;2._______________叫正多边形的中心,______________叫正多边形的半径,____________________叫正多边形的中心角,___________________叫正多边形的边心距。活动三 探索正多边形的对称性正三角形、正方形、正五边形、正六边形、正八边形中,哪些是轴对称图形?哪些是中心对称图形?哪些既是轴对称图形,又是中心对称图形?如果是轴对称图形,画出它的对称轴;如果是中心对称图形,找出它的对称中心。 结论:正n(n为奇数)边形是_________图形,有____条对称轴,其对称轴是___________________;正n(n为偶数)边形既是____图形又是________;有__条对称轴,其对称轴是_________________;其对称中心是___________.活动四 应用例1 有一个亭子(如图)它的地基是半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).例2 求正三角形的内切圆半径、外接圆半径和高的比.【练习】1.下列正多边形中,对称轴条数是6条的为 A.正三角形 B.正方形C.正六边形 D.正五边形2.若正多边形的中心角为,则该正多边形的边数为 .A.8 B.7 C.6 D.53.下列命题中,正确的说法有_________________(填序号).①正多边形的各边相等;②各边相等的多边形是正多边形;③正多边形的各角相等;④各角相等的多边形是正多边形;⑤既是轴对称图形,又是中心对称的多边形是正多边形. 4.如图,在同一平面内,将边长相等的正方形、正五边形的一边重合,那么 .5.如果要画一个正十二边形,那么用量角器将圆_______等分, 每一份的圆心角是_______°.6.已知正六边形的边心距为,则正六边形的边长为______________.7.求出半径为4的圆内接正三角形的边长、边心距和面积. 【补充思考】
【感悟】1.这节课你学到了哪些知识?还有哪些疑惑?2.梳理本节知识结构,建立知识间的联系. 【补充思考】
【检测】1.如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( ).A.60° B.45° C.30° D.22. 2.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB 的度数是( ). A.36° B.60° C.72° D.108°3.如图,将边长相等的正六边形和正五边形的边重合叠放在一起,则的度数是 .4.如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 .5.如图,在半径为10cm的⊙O中作一个正六边形ABCDEF.试求此正六边形的面积.6.如图五边形内接于,.求证:五边形是正五边形.
【作业】A组1.在正五边形的外接圆中,任一边所对的圆周角的度数为 A. B. C. D.或2.若正边形的一个内角为,那么的值为 A.12 B.10 C.8 D.73.如图,在正八边形中,连结,,则的值是 A. B. C. D. 第3题 第4题4.如图,正六边形内接于,连接.则的度数是 A. B. C. D.B组5.如图(1)(2)(3)(4),M、N分别为⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE,…,正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.(1)求图1中∠MON的度数;(2)图2中∠MON的度数为_________;(3)请探究∠MON的度数与正n边形边数n的关系(直接写答案).
PAGE
第5/5页
【回顾】①么叫正多边形?矩形是正多边形吗?菱形呢?正方形呢? ②从你身边举出两三个正多边形的实例,正多边形是轴对称图形吗?是中心对称图形吗?如果是,对称中心在哪里?【导入】数学源于生活,让我们观看下列美丽的图案,感受数学之美.问题1 这些美丽的图案,都是在日常生活中我们经常能看到的、利用正多边形设计的物体.你能从这些图案中找出正多边形来吗? 问题2 你知道正多边形和圆有什么关系吗? 【探究】活动一 观察生活中的一些图形,归纳它们的共同特征,引入正多边形的概念_________________________的多边形叫做正多边形。思考:各边相等的多边形一定是正多边形吗?各角相等的多边形呢?若不是举例说明.总结:各边相等与各角相等必须同时成立的多边形才是正多边形. 活动二 用量角器作正多边形,探索正多边形与圆的内在联系1.用量角器将一个圆n(n≥3)等分,依次连接各等分点所得的n边形是这个圆的____________;圆的内接正n边形将圆______________;2._______________叫正多边形的中心,______________叫正多边形的半径,____________________叫正多边形的中心角,___________________叫正多边形的边心距。活动三 探索正多边形的对称性正三角形、正方形、正五边形、正六边形、正八边形中,哪些是轴对称图形?哪些是中心对称图形?哪些既是轴对称图形,又是中心对称图形?如果是轴对称图形,画出它的对称轴;如果是中心对称图形,找出它的对称中心。 结论:正n(n为奇数)边形是_________图形,有____条对称轴,其对称轴是___________________;正n(n为偶数)边形既是____图形又是________;有__条对称轴,其对称轴是_________________;其对称中心是___________.活动四 应用例1 有一个亭子(如图)它的地基是半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).例2 求正三角形的内切圆半径、外接圆半径和高的比.【练习】1.下列正多边形中,对称轴条数是6条的为 A.正三角形 B.正方形C.正六边形 D.正五边形2.若正多边形的中心角为,则该正多边形的边数为 .A.8 B.7 C.6 D.53.下列命题中,正确的说法有_________________(填序号).①正多边形的各边相等;②各边相等的多边形是正多边形;③正多边形的各角相等;④各角相等的多边形是正多边形;⑤既是轴对称图形,又是中心对称的多边形是正多边形. 4.如图,在同一平面内,将边长相等的正方形、正五边形的一边重合,那么 .5.如果要画一个正十二边形,那么用量角器将圆_______等分, 每一份的圆心角是_______°.6.已知正六边形的边心距为,则正六边形的边长为______________.7.求出半径为4的圆内接正三角形的边长、边心距和面积. 【补充思考】
【感悟】1.这节课你学到了哪些知识?还有哪些疑惑?2.梳理本节知识结构,建立知识间的联系. 【补充思考】
【检测】1.如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( ).A.60° B.45° C.30° D.22. 2.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB 的度数是( ). A.36° B.60° C.72° D.108°3.如图,将边长相等的正六边形和正五边形的边重合叠放在一起,则的度数是 .4.如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 .5.如图,在半径为10cm的⊙O中作一个正六边形ABCDEF.试求此正六边形的面积.6.如图五边形内接于,.求证:五边形是正五边形.
【作业】A组1.在正五边形的外接圆中,任一边所对的圆周角的度数为 A. B. C. D.或2.若正边形的一个内角为,那么的值为 A.12 B.10 C.8 D.73.如图,在正八边形中,连结,,则的值是 A. B. C. D. 第3题 第4题4.如图,正六边形内接于,连接.则的度数是 A. B. C. D.B组5.如图(1)(2)(3)(4),M、N分别为⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE,…,正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.(1)求图1中∠MON的度数;(2)图2中∠MON的度数为_________;(3)请探究∠MON的度数与正n边形边数n的关系(直接写答案).
PAGE
第5/5页
同课章节目录
