24.3 正多边形和圆 第2课时同步导学案(无答案)
文档属性
| 名称 | 24.3 正多边形和圆 第2课时同步导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 490.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:27 | ||
图片预览

文档简介
学习课题:《24.3正多边形和圆(2)》学习目标:1.会用量角器等分圆作任意正多边形;会用尺规作圆内接正方形和正六边形,并且能作圆内接正八边形、正三角形、 正十二边形;2.通过作图的过程,提高学生的几何语言表达能力和合情推理能力.通过画图,培养学生的作图能力及动手操作能力.重点知识:会用量角器或尺规作图等分圆周作圆内接正方形和正六边形.难点问题:作图原理的认知.学习策略指导:在学习之前要回顾量角器画角的基本方法与规范,复习尺规画垂线的基本方法,以及正六边形的半径与边长之间的关系;等分圆周法是一种作正多边形的常见方法,通过作简单的正三角形、正方形、正六边形,一直推广到作正八边形的情况,可以体会极限的思想. 【补充思考】
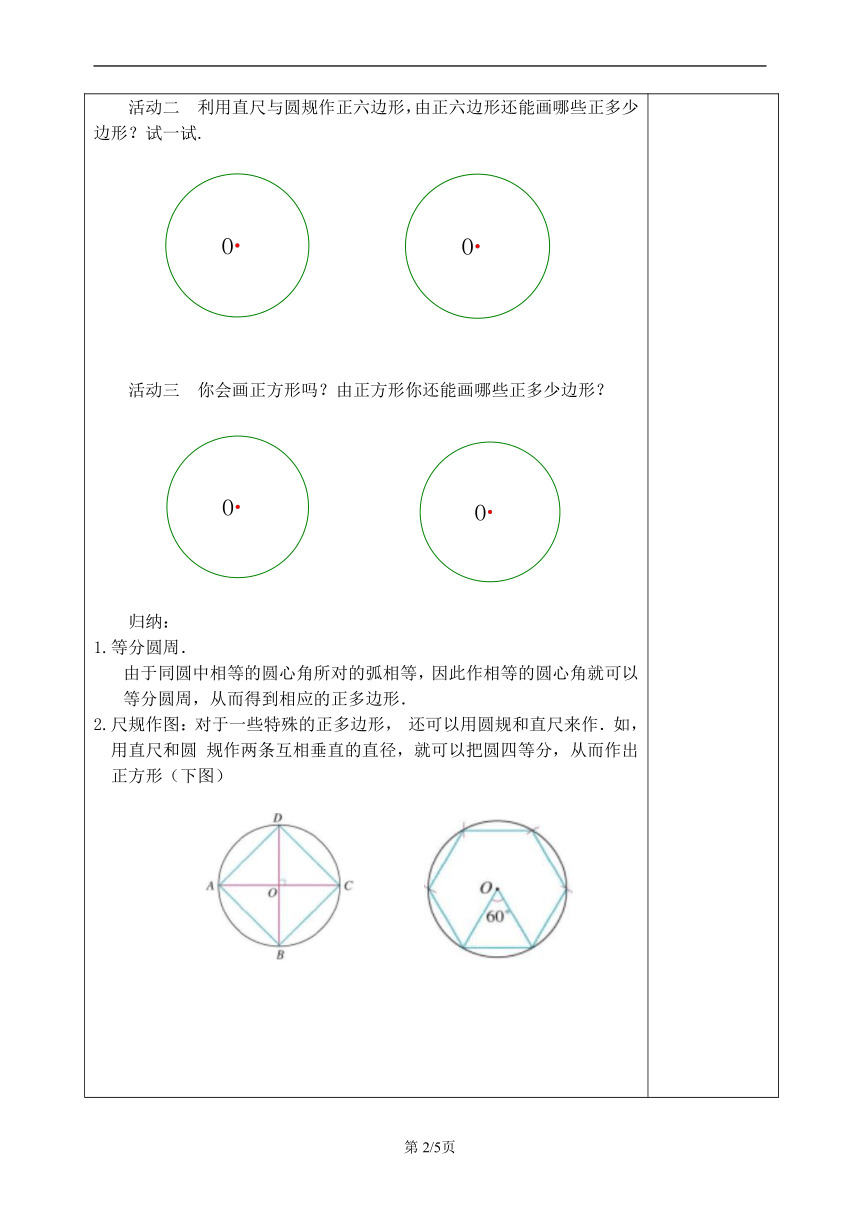
【回顾】1.什么是正多边形?怎么证明一个多边形是正多边形? 2.多边形的内角和怎么计算?正多边形的每一个内角怎么计算? 3.正多边形的半径、中心角、边心距是如何定义的?正多边形的中心角怎么计算?【导入】实际生活中,经常遇到画正多边形的问题,比如画一个六角螺帽的平面图、画一个五角星等,这些问题都与等分圆周有关. 【探究】1.现在我们要画半径为2cm的正六边形,从正多边形与圆的关系可知,只要把半径为______的圆______等分,然后依次连结_______________就得正六边形.2.把半径为2cm的圆六等分,只要把________的圆心角_______等份,即正六边形的中心角=________活动一 用量角器六等分圆,画出半径为2cm的正六边形,作正六边形中心角=________. 结论:用_______________的方法,可以作任意正n边形活动二 利用直尺与圆规作正六边形,由正六边形还能画哪些正多少边形?试一试.活动三 你会画正方形吗?由正方形你还能画哪些正多少边形? 归纳:1.等分圆周. 由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角就可以等分圆周,从而得到相应的正多边形. 2.尺规作图:对于一些特殊的正多边形, 还可以用圆规和直尺来作.如,用直尺和圆 规作两条互相垂直的直径,就可以把圆四等分,从而作出正方形(下图) 【练习】1.要把一个圆周8等分,每一段弧所对的圆心角的度数为______,顺次连接各分点得到正 .2.把一个圆周10等分,顺次连接各分点,所得四边形是什么形状?为什么?3.能用圆规和直尺画一个正三角形吗? 4.实例探究:用等分圆周的方法画出下列图案. 【补充思考】
【感悟】1.这堂课你学了哪些知识?(1)用量角器等分圆周作任意正n边形;(2)用尺规作正方形及由此扩展作正八边形、用尺规作正六边形及由此扩展作正12边形、正三角形).你收获了哪些方法和经验? 【补充思考】
【检测】1.四边形ABCD为⊙O的内接梯形,如图所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是______;△ODA的周长是_______;∠BOC的度数是________.2.如果要画一个正十二边形,那么用量角器将圆____等分,每一份的圆心角是____.借助量角器画一个正十二边形.3.画一个半径为2cm的正五边形,再作出这个正五边形的各条对角线,画一个五角星.4.已知⊙O和⊙O上的一点A(如图). (1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;(2)在(1)题的作图中,如果点E在弧AD上,求证:DE是⊙O内接正十二边形的一边.
【作业】A组1.若一个圆内接正多边形的中心角是,则这个多边形是 A.正五边形 B.正八边形 C.正十边形 D.正十八边形2.正六边形的边长与边心距之比为 A. B. C. D.3.已知圆的内接正六边形的面积为,则该圆的半径等于 A. B. C. D.4.已知等边三角形的内切圆半径,外接圆半径和高的比是 A. B. C. D.B组5.半径为的圆内接正三角形、正方形、正六边形的边心距分别为,,,则,,的大小关系是 A. B. C. D.6.若一个正多边形的一个外角为,边心距为.则它的外接圆半径为 .7.你能进一步只用直尺和圆规画出正十二边形、正十二边形吗?试一试.8.如图,在半径为的圆中作一个正六边形,试求此正六边形的面积.
PAGE
第5/5页
【回顾】1.什么是正多边形?怎么证明一个多边形是正多边形? 2.多边形的内角和怎么计算?正多边形的每一个内角怎么计算? 3.正多边形的半径、中心角、边心距是如何定义的?正多边形的中心角怎么计算?【导入】实际生活中,经常遇到画正多边形的问题,比如画一个六角螺帽的平面图、画一个五角星等,这些问题都与等分圆周有关. 【探究】1.现在我们要画半径为2cm的正六边形,从正多边形与圆的关系可知,只要把半径为______的圆______等分,然后依次连结_______________就得正六边形.2.把半径为2cm的圆六等分,只要把________的圆心角_______等份,即正六边形的中心角=________活动一 用量角器六等分圆,画出半径为2cm的正六边形,作正六边形中心角=________. 结论:用_______________的方法,可以作任意正n边形活动二 利用直尺与圆规作正六边形,由正六边形还能画哪些正多少边形?试一试.活动三 你会画正方形吗?由正方形你还能画哪些正多少边形? 归纳:1.等分圆周. 由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角就可以等分圆周,从而得到相应的正多边形. 2.尺规作图:对于一些特殊的正多边形, 还可以用圆规和直尺来作.如,用直尺和圆 规作两条互相垂直的直径,就可以把圆四等分,从而作出正方形(下图) 【练习】1.要把一个圆周8等分,每一段弧所对的圆心角的度数为______,顺次连接各分点得到正 .2.把一个圆周10等分,顺次连接各分点,所得四边形是什么形状?为什么?3.能用圆规和直尺画一个正三角形吗? 4.实例探究:用等分圆周的方法画出下列图案. 【补充思考】
【感悟】1.这堂课你学了哪些知识?(1)用量角器等分圆周作任意正n边形;(2)用尺规作正方形及由此扩展作正八边形、用尺规作正六边形及由此扩展作正12边形、正三角形).你收获了哪些方法和经验? 【补充思考】
【检测】1.四边形ABCD为⊙O的内接梯形,如图所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是______;△ODA的周长是_______;∠BOC的度数是________.2.如果要画一个正十二边形,那么用量角器将圆____等分,每一份的圆心角是____.借助量角器画一个正十二边形.3.画一个半径为2cm的正五边形,再作出这个正五边形的各条对角线,画一个五角星.4.已知⊙O和⊙O上的一点A(如图). (1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;(2)在(1)题的作图中,如果点E在弧AD上,求证:DE是⊙O内接正十二边形的一边.
【作业】A组1.若一个圆内接正多边形的中心角是,则这个多边形是 A.正五边形 B.正八边形 C.正十边形 D.正十八边形2.正六边形的边长与边心距之比为 A. B. C. D.3.已知圆的内接正六边形的面积为,则该圆的半径等于 A. B. C. D.4.已知等边三角形的内切圆半径,外接圆半径和高的比是 A. B. C. D.B组5.半径为的圆内接正三角形、正方形、正六边形的边心距分别为,,,则,,的大小关系是 A. B. C. D.6.若一个正多边形的一个外角为,边心距为.则它的外接圆半径为 .7.你能进一步只用直尺和圆规画出正十二边形、正十二边形吗?试一试.8.如图,在半径为的圆中作一个正六边形,试求此正六边形的面积.
PAGE
第5/5页
同课章节目录
