24章圆检测(无答案)
图片预览

文档简介
人教版·九年级·数学·教与学 第16/16课时/第24章
2020/2021学年度第一学期 编写 宋国平
24章圆单元测试题
一、选择题:(每小题3分 ,共30分)
1.下列命题:①半圆所对的弦是直径,直径所对的弧是半圆;②平分弦的直径垂直于弦,并且垂直于弦所对的弧;③两条弦相等,它们所对的圆心角相等;④到圆心距离等于半径的直线是圆的切线;其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
2.如图;如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中错误的是( )
A.CE=DE B. C.∠BAC=∠BAD D.AC>AD
3.⊙O的半径是3cm,直线l上有一点P到点O的距离为3cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.相交或相切
4.在半径为8cm的圆中,垂直平分半径的弦长为( )
A. B. C.4cm D.8cm
5.若一个扇形的面积是12π,它的弧长是4π,则它的半径是( )
A.3 B.4 C.5 D.6
6.如图,△ABC内接于⊙O,连结OA、OB,若∠ABO=25°,则∠C的度数为( ).
A.55° B.60° C.65° D.70°
7.如图,将半径为的圆形纸片折叠后,圆弧恰好经过圆心,则折痕的长为( )
A、 B、 C、 D、
8.如图,已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若,则BD的长为( )
A. B. C. D.
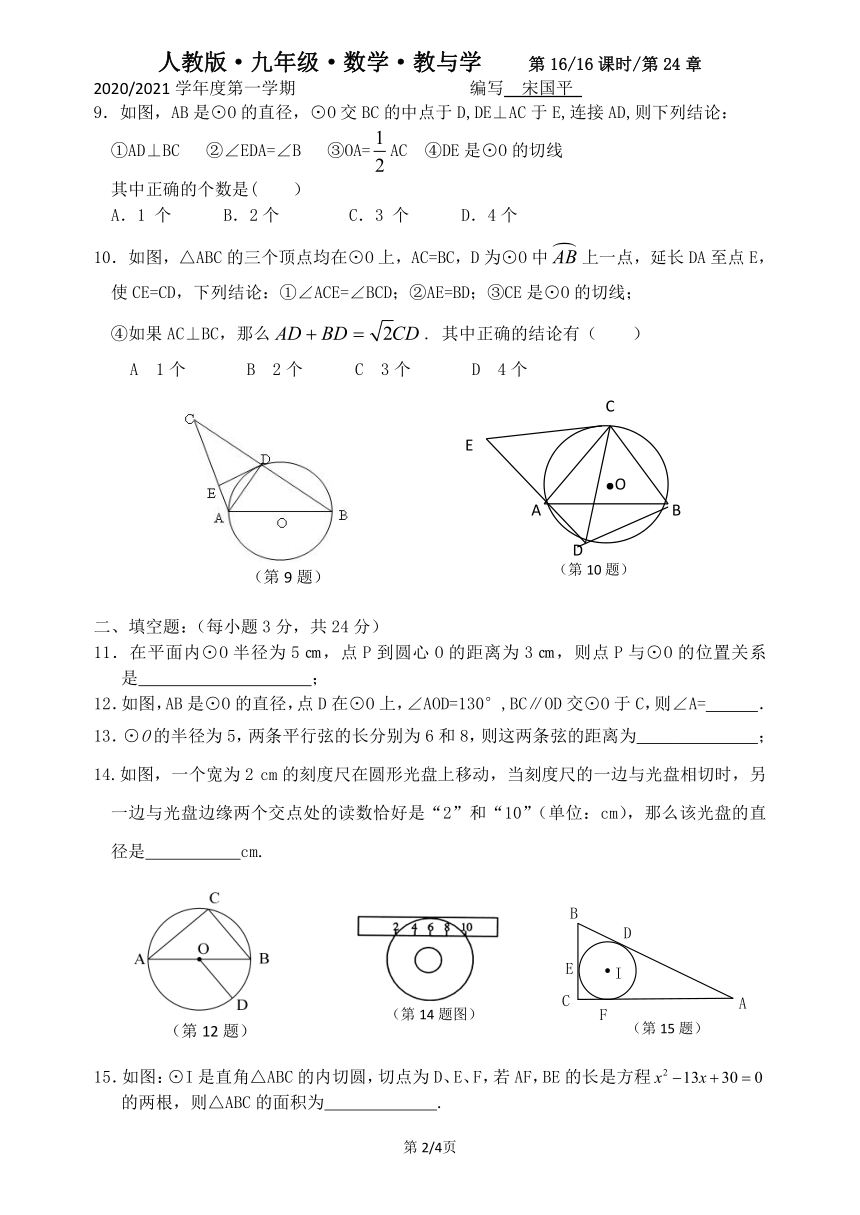
9.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC ②∠EDA=∠B ③OA=AC ④DE是⊙O的切线
其中正确的个数是( )
A.1 个 B.2个 C.3 个 D.4个
10.如图,△ABC的三个顶点均在⊙O上,AC=BC,D为⊙O中上一点,延长DA至点E,
使CE=CD,下列结论:①∠ACE=∠BCD;②AE=BD;③CE是⊙O的切线;
④如果AC⊥BC,那么. 其中正确的结论有( )
A 1个 B 2个 C 3个 D 4个
二、填空题:(每小题3分,共24分)
11.在平面内⊙O半径为5㎝,点P到圆心O的距离为3㎝,则点P与⊙O的位置关系是 ;
12.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于C,则∠A= .
13.⊙O的半径为5,两条平行弦的长分别为6和8,则这两条弦的距离为 ;
14.如图,一个宽为2 cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是 cm.
15.如图:⊙I是直角△ABC的内切圆,切点为D、E、F,若AF,BE的长是方程的两根,则△ABC的面积为 .
16.如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数的图像过点P,则= .
17. 如图,为与圆O的重迭情形,其中BC为圆O的直径。若,BC=2,则图中阴影区域的面积为______________.
18.如图:圆锥的侧面积恰好等于其底面积的2倍,则该圆锥的侧面展开图所对应的扇形圆心角的度数为 .
三、解答题:(本题共66分)
19.(10分)如图,AB是⊙O的直径,C为⊙O上的一点,AD和过C的切线互相垂直,垂足为D,求证:AC平分∠DAB.
20.(10分)如图所示,AD是⊙O的直径,AC为弦,∠CAD=30°,OB⊥AD于O,交AC于B,AB=5,求BC的长.
21.(14分) 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1) 求证:直线PB与⊙O相切;
(2) PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
22. (16分)已知:如图,在锐角∠MAN的边AN上取一点B,
以AB为直径的半圆O交AM于C,交∠MAN的角平分线
于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN
于F.(1)猜想ED与⊙O的位置关系,并说明理由;
(2)若∠MAN=60°,AE=,求阴影部分的面积.
23.(16分)如图10,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5㎝,AC=8㎝,求⊙O的半径.
(第8题图)
O
A
B
(第7题图)
(第6题图)
(第9题)
A
E
D
C
B
●O
(第10题)
(第14题图)
(第15题)
(第12题)
O
P
M
A
N
(第16题)
(第18题图)
(第17题图)
PAGE
第1/4页
2020/2021学年度第一学期 编写 宋国平
24章圆单元测试题
一、选择题:(每小题3分 ,共30分)
1.下列命题:①半圆所对的弦是直径,直径所对的弧是半圆;②平分弦的直径垂直于弦,并且垂直于弦所对的弧;③两条弦相等,它们所对的圆心角相等;④到圆心距离等于半径的直线是圆的切线;其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
2.如图;如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中错误的是( )
A.CE=DE B. C.∠BAC=∠BAD D.AC>AD
3.⊙O的半径是3cm,直线l上有一点P到点O的距离为3cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.相交或相切
4.在半径为8cm的圆中,垂直平分半径的弦长为( )
A. B. C.4cm D.8cm
5.若一个扇形的面积是12π,它的弧长是4π,则它的半径是( )
A.3 B.4 C.5 D.6
6.如图,△ABC内接于⊙O,连结OA、OB,若∠ABO=25°,则∠C的度数为( ).
A.55° B.60° C.65° D.70°
7.如图,将半径为的圆形纸片折叠后,圆弧恰好经过圆心,则折痕的长为( )
A、 B、 C、 D、
8.如图,已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若,则BD的长为( )
A. B. C. D.
9.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC ②∠EDA=∠B ③OA=AC ④DE是⊙O的切线
其中正确的个数是( )
A.1 个 B.2个 C.3 个 D.4个
10.如图,△ABC的三个顶点均在⊙O上,AC=BC,D为⊙O中上一点,延长DA至点E,
使CE=CD,下列结论:①∠ACE=∠BCD;②AE=BD;③CE是⊙O的切线;
④如果AC⊥BC,那么. 其中正确的结论有( )
A 1个 B 2个 C 3个 D 4个
二、填空题:(每小题3分,共24分)
11.在平面内⊙O半径为5㎝,点P到圆心O的距离为3㎝,则点P与⊙O的位置关系是 ;
12.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于C,则∠A= .
13.⊙O的半径为5,两条平行弦的长分别为6和8,则这两条弦的距离为 ;
14.如图,一个宽为2 cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是 cm.
15.如图:⊙I是直角△ABC的内切圆,切点为D、E、F,若AF,BE的长是方程的两根,则△ABC的面积为 .
16.如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数的图像过点P,则= .
17. 如图,为与圆O的重迭情形,其中BC为圆O的直径。若,BC=2,则图中阴影区域的面积为______________.
18.如图:圆锥的侧面积恰好等于其底面积的2倍,则该圆锥的侧面展开图所对应的扇形圆心角的度数为 .
三、解答题:(本题共66分)
19.(10分)如图,AB是⊙O的直径,C为⊙O上的一点,AD和过C的切线互相垂直,垂足为D,求证:AC平分∠DAB.
20.(10分)如图所示,AD是⊙O的直径,AC为弦,∠CAD=30°,OB⊥AD于O,交AC于B,AB=5,求BC的长.
21.(14分) 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1) 求证:直线PB与⊙O相切;
(2) PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
22. (16分)已知:如图,在锐角∠MAN的边AN上取一点B,
以AB为直径的半圆O交AM于C,交∠MAN的角平分线
于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN
于F.(1)猜想ED与⊙O的位置关系,并说明理由;
(2)若∠MAN=60°,AE=,求阴影部分的面积.
23.(16分)如图10,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5㎝,AC=8㎝,求⊙O的半径.
(第8题图)
O
A
B
(第7题图)
(第6题图)
(第9题)
A
E
D
C
B
●O
(第10题)
(第14题图)
(第15题)
(第12题)
O
P
M
A
N
(第16题)
(第18题图)
(第17题图)
PAGE
第1/4页
同课章节目录
