同步导学案25.3用频率估计概率1(无答案)
文档属性
| 名称 | 同步导学案25.3用频率估计概率1(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 86.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:43 | ||
图片预览


文档简介
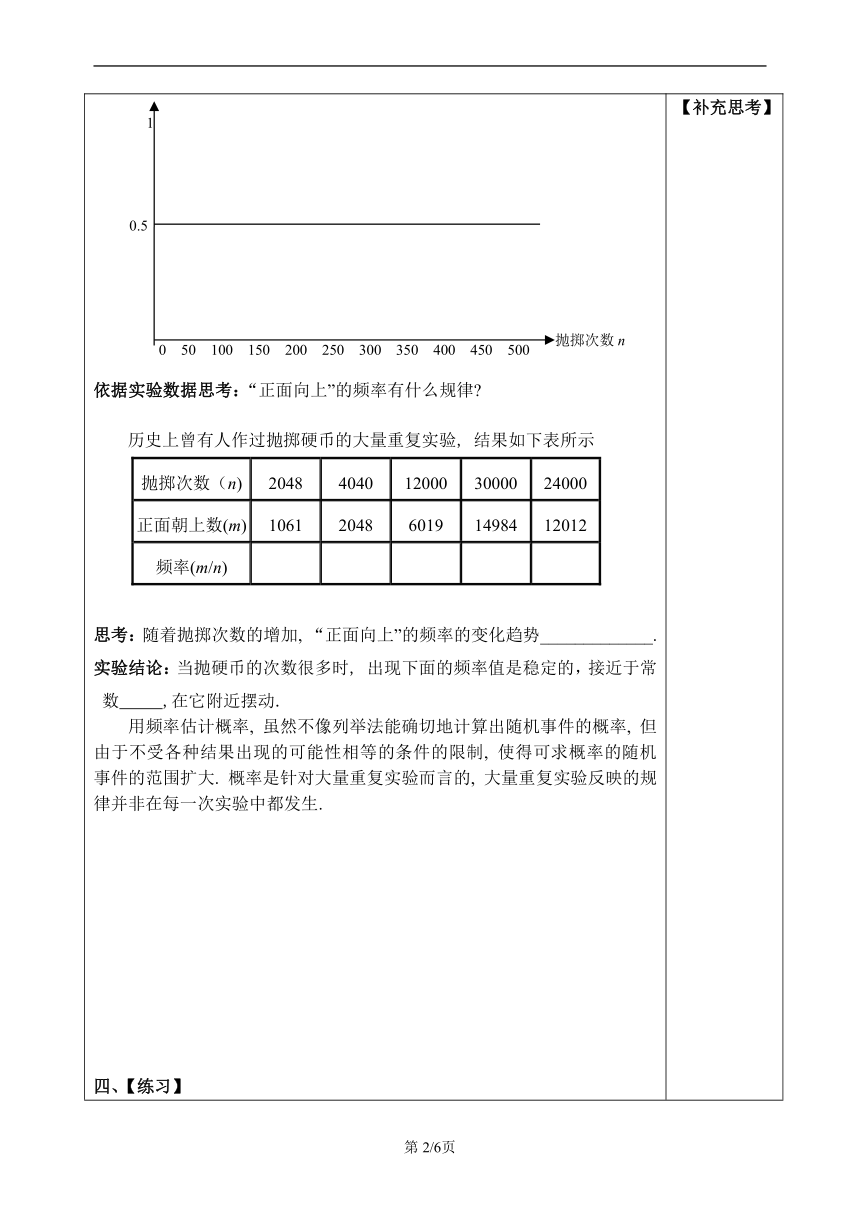
学习课题:《25.3用频率估计概率 》第1课时学习目标:1. 理解实验次数较大时实验频率趋于稳定这一规律.2. 结合具体情景掌握如何用频率估计概率.3. 通过概率计算进一步比较概率与频率之间的关系.重点知识:通过对事件发生的频率的分析来估计事件发生的概率 难点问题:比较用列举法求概率与用频率求概率的条件与方法.学习策略指导:用频率估计概率的正确性、近似性. 正确性是在相同的条件下,大量重复的实验下,频率可以认为是事件的概率,运用这个概率去估计事件发生的可能性. 近似性是因为这个概率毕竟是通过实验统计出来的, 不同的人实验的结果可能不一样, 不同的实验次数实验的结果可能不一样. 【补充思考】
一、【回顾】1 用列举法求概率的条件是什么 2.用列举法求概率的方法有哪些 3.P(A)的取值范围是什么 4.如图, A、B两个转盘分别被平均分成三个、四个扇形, 分别转动A盘、B盘各一次. 转动过程中, 指针保持不动, 如果指针恰好指在分割线上, 则重转一次, 直到指针指向一个数字所在的区域为止. 请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率.二、【导入】:抛掷一枚质地均匀的硬币时,“正面向上”和“反面向上”发生的可能性相等, 这两个随机事件发生的概率都是0.5. 这是否意味着抛掷一枚硬币100次时, 就会有50次“正面向上”和50次“反面向上”呢 三、【探究】试验:把全班同学分成10组, 每组同学掷一枚硬币50次, 整理获得的试验数据, 并记录在下表: 投掷次数n50100150200250300350400450500正面朝上的次数m24527399124146180201229256正面朝上的频率m/n根据上表中的数据,标注出对应的点:依据实验数据思考:“正面向上”的频率有什么规律 历史上曾有人作过抛掷硬币的大量重复实验, 结果如下表所示抛掷次数(n)20484040120003000024000正面朝上数(m)1061204860191498412012频率(m/n)思考:随着抛掷次数的增加, “正面向上”的频率的变化趋势_____________.实验结论:当抛硬币的次数很多时, 出现下面的频率值是稳定的,接近于常数 ,在它附近摆动.用频率估计概率, 虽然不像列举法能确切地计算出随机事件的概率, 但由于不受各种结果出现的可能性相等的条件的限制, 使得可求概率的随机事件的范围扩大. 概率是针对大量重复实验而言的, 大量重复实验反映的规律并非在每一次实验中都发生.四、【练习】1.盒子中有白色乒乓球8个和黄色乒乓球若干个, 为求得盒中黄色乒乓球的个数, 某同学进行了如下实验:每次摸出一个乒乓球记下它的颜色, 如此重复360次, 摸出白色乒乓球90次, 则黄色乒乓球的个数估计为( )A.90个 B.24个 C.70个 D.32个2.下表记录了一名球员在罚球线上投篮的结果.投篮次数(n)50100150200250300500投中次数(m)286078104123152251投中频率(m/n)(1)计算表中的投中频率(精确到0.01);(2)这名球员投篮一次,投中的概率约是多少?(精确到0.1)?3.一个口袋中放有20个球, 其中红球6个, 白球和黑球若干个, 每个球除了颜色外没有任何区别: (1)小王通过大量反复试验(每次取一个球, 放回搅匀后再取)发现, 取出黑球的频率稳定在1/4左右, 请你估计袋中黑球的个数. (2)若小王取出的第一个是白球, 将它放在桌上, 从袋中余下的球中再任意取一个球, 取出红球的概率是多少 五、【感悟】这节课有什么收获?请把它写下来吧!待解决的问题:六、【检测】1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾, 一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%, 则这个水塘里有鲤鱼_______尾, 鲢鱼_______尾.2.某口袋中有红色、黄色、蓝色玻璃共72个, 小明通过多次摸球试验后, 发现摸到红球、黄球、蓝球的频率为35%, 25%和40%, 估计口袋中黄色玻璃球有_____个.3.在种子发芽率的实验中, 科研人员经过大量实验得到不同数量的种子, 发芽的频率都约是0.78, 则可以估计种子发芽率是 ( ) , 从而可估计200千克的种子约有 ( )千克种子发芽.4.某笔芯厂生产圆珠笔芯, 每箱可装2000支.一位质检员误把一些已做标记的不合格产品也放入箱子里, 若随机拿出100支, 共做10次实验, 这100支中不合格笔芯的平均数是5, 你能估计箱子里有多少支不合格品吗 若每支合格品的利润为0.5元,如果顾客发现不合格品, 需双倍赔偿(即每支赔1元), 如果让这箱含不合格品的笔芯走上市场, 根据你的估算这箱笔芯是赚是赔 赚多少或赔多少 七、【作业】A组1.下列说法不正确的是( )A.增加几次试验,事件发生的频率与这一事件发生的概率的差距可能扩大B.增加几次试验,事件发生的频率与这一事件发生的概率的差距可能缩小C.试验次数很大时,事件发生的频率稳定在这一事件发生的概率附近 D.试验次数增大时,事件发生的频率越来越接近这一事件发生的概率2.某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )A.掷一枚质地均匀的硬币,落地时结果是“正面向上” B.掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6 C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” D.袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球3.用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,下列说法正确的是( )A.种植10棵幼树,结果一定是“有9棵幼树成活” B.种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活”C.种植10n棵幼树,恰好有“n棵幼树不成活” D.种植n棵幼树,n越来越大时,种植成活幼树的频率会越来越稳定于0.94.在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,则估计盒子中大约有红球( )A.16个 B.14个 C.20个 D.30个5.两个人做掷硬币的游戏,掷出正面甲得1分,掷出反面乙得1分,先得3分的人赢得一个大蛋糕,游戏因故中途结束,此时甲得2分,乙得1分,若此时分配蛋糕,甲应分得蛋糕的 .B组6.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .7.在一个不透明的袋中装有若干个材质、大小完全相同的红球,小明在袋中放入3个黑球(每个黑球除颜色外其余都与红球相同),摇匀后每次随机从袋中摸出一个球,记录颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,估计袋中红球有 个.8.小明做投掷骰子(质地均匀的正方体)实验,共做了100次实验,实验的结果如下:朝上的点数123456出现的次数141523162012(1)计算“4点朝上”的频率.(2)小明说:“根据实验,一次实验中出现3点朝上的概率最大”.他的说法正确吗?为什么?(3)小明投掷一枚骰子,计算投掷点数小于3的概率. 【补充思考】【补充思考】【补充思考】
0
1
2
3
4
53333
6
A
B
抛掷次数n
0 50 100 150 200 250 300 350 400 450 500
0.5
1
PAGE
第6/6页
一、【回顾】1 用列举法求概率的条件是什么 2.用列举法求概率的方法有哪些 3.P(A)的取值范围是什么 4.如图, A、B两个转盘分别被平均分成三个、四个扇形, 分别转动A盘、B盘各一次. 转动过程中, 指针保持不动, 如果指针恰好指在分割线上, 则重转一次, 直到指针指向一个数字所在的区域为止. 请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率.二、【导入】:抛掷一枚质地均匀的硬币时,“正面向上”和“反面向上”发生的可能性相等, 这两个随机事件发生的概率都是0.5. 这是否意味着抛掷一枚硬币100次时, 就会有50次“正面向上”和50次“反面向上”呢 三、【探究】试验:把全班同学分成10组, 每组同学掷一枚硬币50次, 整理获得的试验数据, 并记录在下表: 投掷次数n50100150200250300350400450500正面朝上的次数m24527399124146180201229256正面朝上的频率m/n根据上表中的数据,标注出对应的点:依据实验数据思考:“正面向上”的频率有什么规律 历史上曾有人作过抛掷硬币的大量重复实验, 结果如下表所示抛掷次数(n)20484040120003000024000正面朝上数(m)1061204860191498412012频率(m/n)思考:随着抛掷次数的增加, “正面向上”的频率的变化趋势_____________.实验结论:当抛硬币的次数很多时, 出现下面的频率值是稳定的,接近于常数 ,在它附近摆动.用频率估计概率, 虽然不像列举法能确切地计算出随机事件的概率, 但由于不受各种结果出现的可能性相等的条件的限制, 使得可求概率的随机事件的范围扩大. 概率是针对大量重复实验而言的, 大量重复实验反映的规律并非在每一次实验中都发生.四、【练习】1.盒子中有白色乒乓球8个和黄色乒乓球若干个, 为求得盒中黄色乒乓球的个数, 某同学进行了如下实验:每次摸出一个乒乓球记下它的颜色, 如此重复360次, 摸出白色乒乓球90次, 则黄色乒乓球的个数估计为( )A.90个 B.24个 C.70个 D.32个2.下表记录了一名球员在罚球线上投篮的结果.投篮次数(n)50100150200250300500投中次数(m)286078104123152251投中频率(m/n)(1)计算表中的投中频率(精确到0.01);(2)这名球员投篮一次,投中的概率约是多少?(精确到0.1)?3.一个口袋中放有20个球, 其中红球6个, 白球和黑球若干个, 每个球除了颜色外没有任何区别: (1)小王通过大量反复试验(每次取一个球, 放回搅匀后再取)发现, 取出黑球的频率稳定在1/4左右, 请你估计袋中黑球的个数. (2)若小王取出的第一个是白球, 将它放在桌上, 从袋中余下的球中再任意取一个球, 取出红球的概率是多少 五、【感悟】这节课有什么收获?请把它写下来吧!待解决的问题:六、【检测】1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾, 一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%, 则这个水塘里有鲤鱼_______尾, 鲢鱼_______尾.2.某口袋中有红色、黄色、蓝色玻璃共72个, 小明通过多次摸球试验后, 发现摸到红球、黄球、蓝球的频率为35%, 25%和40%, 估计口袋中黄色玻璃球有_____个.3.在种子发芽率的实验中, 科研人员经过大量实验得到不同数量的种子, 发芽的频率都约是0.78, 则可以估计种子发芽率是 ( ) , 从而可估计200千克的种子约有 ( )千克种子发芽.4.某笔芯厂生产圆珠笔芯, 每箱可装2000支.一位质检员误把一些已做标记的不合格产品也放入箱子里, 若随机拿出100支, 共做10次实验, 这100支中不合格笔芯的平均数是5, 你能估计箱子里有多少支不合格品吗 若每支合格品的利润为0.5元,如果顾客发现不合格品, 需双倍赔偿(即每支赔1元), 如果让这箱含不合格品的笔芯走上市场, 根据你的估算这箱笔芯是赚是赔 赚多少或赔多少 七、【作业】A组1.下列说法不正确的是( )A.增加几次试验,事件发生的频率与这一事件发生的概率的差距可能扩大B.增加几次试验,事件发生的频率与这一事件发生的概率的差距可能缩小C.试验次数很大时,事件发生的频率稳定在这一事件发生的概率附近 D.试验次数增大时,事件发生的频率越来越接近这一事件发生的概率2.某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )A.掷一枚质地均匀的硬币,落地时结果是“正面向上” B.掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6 C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” D.袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球3.用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,下列说法正确的是( )A.种植10棵幼树,结果一定是“有9棵幼树成活” B.种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活”C.种植10n棵幼树,恰好有“n棵幼树不成活” D.种植n棵幼树,n越来越大时,种植成活幼树的频率会越来越稳定于0.94.在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,则估计盒子中大约有红球( )A.16个 B.14个 C.20个 D.30个5.两个人做掷硬币的游戏,掷出正面甲得1分,掷出反面乙得1分,先得3分的人赢得一个大蛋糕,游戏因故中途结束,此时甲得2分,乙得1分,若此时分配蛋糕,甲应分得蛋糕的 .B组6.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .7.在一个不透明的袋中装有若干个材质、大小完全相同的红球,小明在袋中放入3个黑球(每个黑球除颜色外其余都与红球相同),摇匀后每次随机从袋中摸出一个球,记录颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.85左右,估计袋中红球有 个.8.小明做投掷骰子(质地均匀的正方体)实验,共做了100次实验,实验的结果如下:朝上的点数123456出现的次数141523162012(1)计算“4点朝上”的频率.(2)小明说:“根据实验,一次实验中出现3点朝上的概率最大”.他的说法正确吗?为什么?(3)小明投掷一枚骰子,计算投掷点数小于3的概率. 【补充思考】【补充思考】【补充思考】
0
1
2
3
4
53333
6
A
B
抛掷次数n
0 50 100 150 200 250 300 350 400 450 500
0.5
1
PAGE
第6/6页
同课章节目录
