同步导学案27.2.1相似三角形的判定第1课时学案 (无答案)
文档属性
| 名称 | 同步导学案27.2.1相似三角形的判定第1课时学案 (无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 775.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:43 | ||
图片预览

文档简介
学习课题:《27.2.1相似三角形的判定(一)》学习目标:1.记住两个三角形相似的判定条件(三个角对应相等,三条边的比对应相等,则两个三角形相似)——相似三角形的定义,和三角形相似的预备定理(平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似).2.经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,进一步发展学生的探究、交流能力.3.会运用“两个三角形相似的判定条件”和“三角形相似的预备定理”解决简单的问题.重点知识:相似三角形的定义与三角形相似的预备定理.难点问题:三角形相似的预备定理的应用.学习策略指导:通读教材,认真测量计算,多次重复,从而达到对基本事实的认识.如果会使用几何画板等软件,要通过几何画板进行验证.平行线分线段成比例的基本事实,结论多,容易乱,可以用:,等语言叙述,可以更好的找出所有的比例式. 【补充思考】
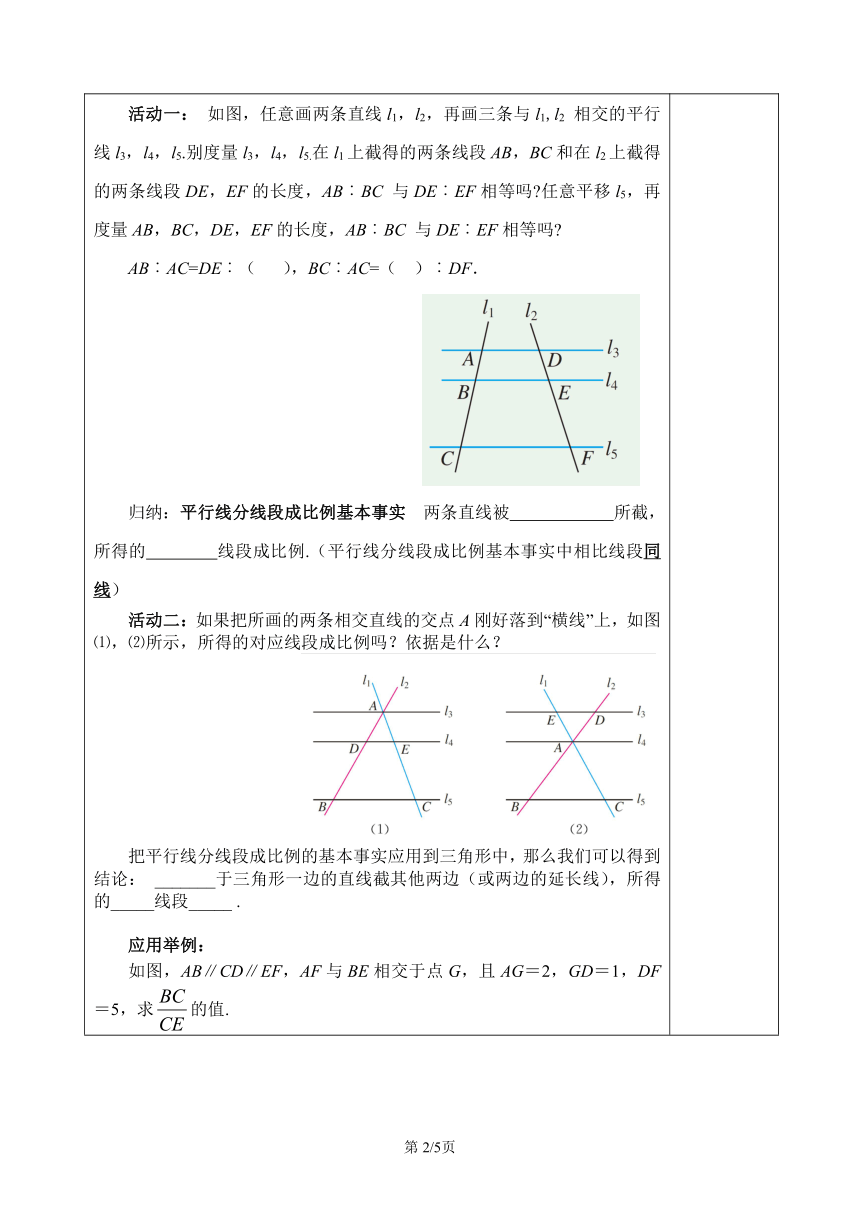
【回顾】1.什么叫做相似多边形?2.相似多边形的性质和判定各是什么?【导入】1.在相似多边形中,最简单的就是相似三角形.在△ABC与△A′B′C′中,如果∠A=∠A′, ∠B=∠B′, ∠C=∠C′, 且. 我们就说△ABC与△A′B′C′相似,记作△ABC∽△A′B′C′,k就是它们的相似比.反之如果△ABC∽△A′B′C′,则有∠A=∠A′, ∠B=∠B′, ∠C=∠C′, 且. 2.问题:如果k=1,这两个三角形有怎样的关系?【探究】活动一: 如图,任意画两条直线l1,l2,再画三条与l1,l2 相交的平行线l3,l4,l5.别度量l3,l4,l5.在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,AB︰BC 与DE︰EF相等吗 任意平移l5,再度量AB,BC,DE,EF的长度,AB︰BC 与DE︰EF相等吗 AB︰AC=DE︰( ),BC︰AC=( )︰DF.归纳:平行线分线段成比例基本事实 两条直线被 所截,所得的 线段成比例.(平行线分线段成比例基本事实中相比线段同线) 活动二:如果把所画的两条相交直线的交点A刚好落到“横线”上,如图⑴,⑵所示,所得的对应线段成比例吗?依据是什么?把平行线分线段成比例的基本事实应用到三角形中,那么我们可以得到结论: _______于三角形一边的直线截其他两边(或两边的延长线),所得的_____线段_____ .应用举例:如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,求的值.活动三:如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E.△ADE与△ABC有什么关系?分析:直觉告诉我们,△ADE与△ABC相似,我们通过相似的定义证明它,即证明∠A=∠A, ∠ADE=∠B, ∠AED=∠C,______=_______=.由前面的结论可知,∵DE∥BC∴______=_______.而中的DE不在△ABC的边BC上,不能直接利用前面的结论,但从要证的=可以看出,除DE外,AE,AC,BC都在△ABC的边上,因此只需将DE_______到BC边上去,使得_____=DE,再证明=________就可以了.只要过点E作EF∥AB,交BC于点F,BF就是_____DE所得的线段.请你写出证明过程:结论:判定三角形相似的定理: ,所构成的三角形与原三角形相似.【练习】1.如图AB∥CD∥EF,那么下列结论正确的是( )A. B. C. D.2.如图,AB∥CD,AB=6,CD=9,AD=10,则OD的长是( )A.4 B.5 C.6 D.7 【补充思考】
【感悟】1.你掌握了哪些知识?2.本节课用到的数学思想和方法:3.学习中的困惑: 【补充思考】
【检测】1.已知在△ABC中,D,E分别是AB,BC的中点,ED:AC等于( )A.1:2 B.1:3 C.2:3 D.2:52.如图,在△ABC中,点D,E分别是AB,BC的中点,求证:.3.如图,在△ABC中,DE∥BC ,EF∥AB,AB=4 ,BC=6,DE=2.求EF.【作业】A组:1. 如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=2CE,AB=6,则AD的长为( )A.3 B.4 C.5 D.62. 如图,l1∥l2∥l3,AB=2,BC=4,DB=3,则DE的长为( )A.4 B.5 C.6 D.93. 如图,中,,为上一点,连接交于,已知,,,则 .B组:4. 如图,在中,,,,平分,交边于点,过点作的平行线,交边于点.(1)求线段的长;(2)取线段的中点,连接,交线段于点,延长线段交边于点,求的值.
E
D
C
B
A
C
B
E
D
A
F
PAGE
第5/5页
【回顾】1.什么叫做相似多边形?2.相似多边形的性质和判定各是什么?【导入】1.在相似多边形中,最简单的就是相似三角形.在△ABC与△A′B′C′中,如果∠A=∠A′, ∠B=∠B′, ∠C=∠C′, 且. 我们就说△ABC与△A′B′C′相似,记作△ABC∽△A′B′C′,k就是它们的相似比.反之如果△ABC∽△A′B′C′,则有∠A=∠A′, ∠B=∠B′, ∠C=∠C′, 且. 2.问题:如果k=1,这两个三角形有怎样的关系?【探究】活动一: 如图,任意画两条直线l1,l2,再画三条与l1,l2 相交的平行线l3,l4,l5.别度量l3,l4,l5.在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,AB︰BC 与DE︰EF相等吗 任意平移l5,再度量AB,BC,DE,EF的长度,AB︰BC 与DE︰EF相等吗 AB︰AC=DE︰( ),BC︰AC=( )︰DF.归纳:平行线分线段成比例基本事实 两条直线被 所截,所得的 线段成比例.(平行线分线段成比例基本事实中相比线段同线) 活动二:如果把所画的两条相交直线的交点A刚好落到“横线”上,如图⑴,⑵所示,所得的对应线段成比例吗?依据是什么?把平行线分线段成比例的基本事实应用到三角形中,那么我们可以得到结论: _______于三角形一边的直线截其他两边(或两边的延长线),所得的_____线段_____ .应用举例:如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,求的值.活动三:如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E.△ADE与△ABC有什么关系?分析:直觉告诉我们,△ADE与△ABC相似,我们通过相似的定义证明它,即证明∠A=∠A, ∠ADE=∠B, ∠AED=∠C,______=_______=.由前面的结论可知,∵DE∥BC∴______=_______.而中的DE不在△ABC的边BC上,不能直接利用前面的结论,但从要证的=可以看出,除DE外,AE,AC,BC都在△ABC的边上,因此只需将DE_______到BC边上去,使得_____=DE,再证明=________就可以了.只要过点E作EF∥AB,交BC于点F,BF就是_____DE所得的线段.请你写出证明过程:结论:判定三角形相似的定理: ,所构成的三角形与原三角形相似.【练习】1.如图AB∥CD∥EF,那么下列结论正确的是( )A. B. C. D.2.如图,AB∥CD,AB=6,CD=9,AD=10,则OD的长是( )A.4 B.5 C.6 D.7 【补充思考】
【感悟】1.你掌握了哪些知识?2.本节课用到的数学思想和方法:3.学习中的困惑: 【补充思考】
【检测】1.已知在△ABC中,D,E分别是AB,BC的中点,ED:AC等于( )A.1:2 B.1:3 C.2:3 D.2:52.如图,在△ABC中,点D,E分别是AB,BC的中点,求证:.3.如图,在△ABC中,DE∥BC ,EF∥AB,AB=4 ,BC=6,DE=2.求EF.【作业】A组:1. 如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=2CE,AB=6,则AD的长为( )A.3 B.4 C.5 D.62. 如图,l1∥l2∥l3,AB=2,BC=4,DB=3,则DE的长为( )A.4 B.5 C.6 D.93. 如图,中,,为上一点,连接交于,已知,,,则 .B组:4. 如图,在中,,,,平分,交边于点,过点作的平行线,交边于点.(1)求线段的长;(2)取线段的中点,连接,交线段于点,延长线段交边于点,求的值.
E
D
C
B
A
C
B
E
D
A
F
PAGE
第5/5页
