同步导学案27.2.3相似三角形应用举例2第9课时(无答案)
文档属性
| 名称 | 同步导学案27.2.3相似三角形应用举例2第9课时(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:43 | ||
图片预览


文档简介
学习课题: 《相似三角形应用举例2》学习目标:1.能够运用三角形相似的知识,解决“盲区”问题等一些实际问题;2.通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力;3.培养学生用科学的态度去探索未知世界的理念,激发学生学习数学的热情. 重点知识:运用三角形相似的知识计算“盲区”等实际问题.难点问题:如何在“盲区”等实际问题中构造相似三角形的模型.学习策略指导:先通过“回顾”预习和“导入”问题,明确“视点”、“视线”、“仰角”等概念的含义,然后在深刻理解题意的基础上构造出相似三角形的模型并完成例6的探究,最后通过相关练习进行巩固完善. 【补充思考】
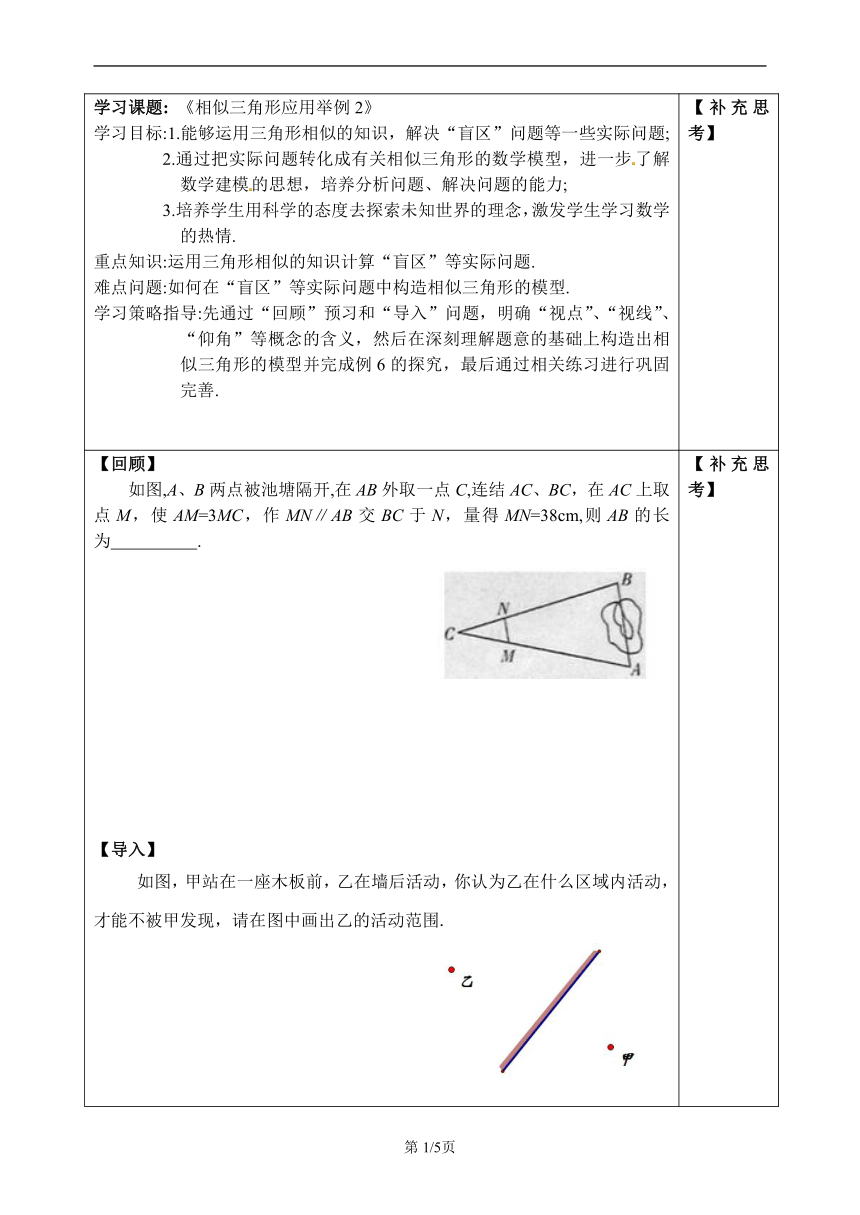
【回顾】如图,A、B两点被池塘隔开,在AB外取一点C,连结AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=38cm,则AB的长为 .【导入】如图,甲站在一座木板前,乙在墙后活动,你认为乙在什么区域内活动,才能不被甲发现,请在图中画出乙的活动范围. 结合上面的图示,填空:1.观察物体时人的眼睛的位置称为 .2.测量物体的高度时,水平视线与向上观察物体的视线间夹角叫做 .3.观察者视线看不到的区域叫做 .4.利用标杆或直尺测量物体的高度时,常常构造 三角形,用相似三角形的性质求物体的高度. 【探究】例6 已知左、右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树根部的距离BD=5 m.一个身高1.6 m的人沿着正对这两棵树的一条水平直路l从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C了 请同学们先阅读例题两遍,阅读时按照后面的要求:(一)阅读题目把相关的数据标在图上.(二)“不能看到右边较高的树的顶端点C”这是真的吗?自学教材40页的分析过程,在图2中找出观察点A和C的仰角.答:(三)继续往前走会出现什么现象 答:(四)如何利用图(2)求EH的长?答:(五)根据上面的结论,你能利用相似三角形和性质,根据已知条件,解决这个问题吗?请写出完整解答过程:【练习】1.利用镜面反射可以计算旗杆的高度,如图,一名同学(用AB表示),站在阳光下,通过镜子C恰好看到旗杆ED的顶端,已知这名同学的身高是1.60米,他到镜子的距离是2米,镜子到旗杆的距离是8米,求旗杆的高. 2.如图,大刚在晚上由灯柱A走向灯柱B,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱A的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱B的底部,已知大刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求两根灯柱之间的距离. 【补充思考】
【感悟】结合本节课的学习目标说一说本节课的收获:本节课我还不明白的有:.利用相似三角形解决“盲区”类实际问题的基本过程: 【补充思考】
【检测】1.甲蹲在地上,乙站在甲和楼之间,两人适当调整自己的位置,当楼顶E,乙的头顶C及甲的眼睛A恰好在一条直线上时,两人分别标定自己的位置B、D,然后测出两人之间的距离BD=1.25m,乙与楼之间的距离DF=30m,(B、D、F在一条直线上),乙的身高CD=1.6m,甲蹲地观测时,眼睛到地面的距离AB=0.8m,你能画出示意图,算出大楼的高度吗?2.如图,花丛中有一路灯杆AB在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
【作业】A组:1.一斜坡长70m,它的高为5m,将某物从斜坡起点推到坡上20m处停止下,停下地点的高度为( ) A. B. C. D. 2.如图所示,一段街道的两边缘所在直线分别为AB,PC,并且AB ∥PC.建筑物DE的一端所在的直线MN垂直AB于点M,交PC于点N.小亮从胜利街的A处,沿AB着方向前进,小明一直站在P点的位置等候小亮.(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点Q标出);(2)已知:MN=20m,MD=8m,PN=24m.求(1)中的Q点到胜利街口的距离QM. B组:3.如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2m的标杆,现测量者从E处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20m,FD=4m,EF=1.8m,求树AB的高度.
PAGE
第1/5页
【回顾】如图,A、B两点被池塘隔开,在AB外取一点C,连结AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=38cm,则AB的长为 .【导入】如图,甲站在一座木板前,乙在墙后活动,你认为乙在什么区域内活动,才能不被甲发现,请在图中画出乙的活动范围. 结合上面的图示,填空:1.观察物体时人的眼睛的位置称为 .2.测量物体的高度时,水平视线与向上观察物体的视线间夹角叫做 .3.观察者视线看不到的区域叫做 .4.利用标杆或直尺测量物体的高度时,常常构造 三角形,用相似三角形的性质求物体的高度. 【探究】例6 已知左、右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树根部的距离BD=5 m.一个身高1.6 m的人沿着正对这两棵树的一条水平直路l从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C了 请同学们先阅读例题两遍,阅读时按照后面的要求:(一)阅读题目把相关的数据标在图上.(二)“不能看到右边较高的树的顶端点C”这是真的吗?自学教材40页的分析过程,在图2中找出观察点A和C的仰角.答:(三)继续往前走会出现什么现象 答:(四)如何利用图(2)求EH的长?答:(五)根据上面的结论,你能利用相似三角形和性质,根据已知条件,解决这个问题吗?请写出完整解答过程:【练习】1.利用镜面反射可以计算旗杆的高度,如图,一名同学(用AB表示),站在阳光下,通过镜子C恰好看到旗杆ED的顶端,已知这名同学的身高是1.60米,他到镜子的距离是2米,镜子到旗杆的距离是8米,求旗杆的高. 2.如图,大刚在晚上由灯柱A走向灯柱B,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱A的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱B的底部,已知大刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求两根灯柱之间的距离. 【补充思考】
【感悟】结合本节课的学习目标说一说本节课的收获:本节课我还不明白的有:.利用相似三角形解决“盲区”类实际问题的基本过程: 【补充思考】
【检测】1.甲蹲在地上,乙站在甲和楼之间,两人适当调整自己的位置,当楼顶E,乙的头顶C及甲的眼睛A恰好在一条直线上时,两人分别标定自己的位置B、D,然后测出两人之间的距离BD=1.25m,乙与楼之间的距离DF=30m,(B、D、F在一条直线上),乙的身高CD=1.6m,甲蹲地观测时,眼睛到地面的距离AB=0.8m,你能画出示意图,算出大楼的高度吗?2.如图,花丛中有一路灯杆AB在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
【作业】A组:1.一斜坡长70m,它的高为5m,将某物从斜坡起点推到坡上20m处停止下,停下地点的高度为( ) A. B. C. D. 2.如图所示,一段街道的两边缘所在直线分别为AB,PC,并且AB ∥PC.建筑物DE的一端所在的直线MN垂直AB于点M,交PC于点N.小亮从胜利街的A处,沿AB着方向前进,小明一直站在P点的位置等候小亮.(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点Q标出);(2)已知:MN=20m,MD=8m,PN=24m.求(1)中的Q点到胜利街口的距离QM. B组:3.如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2m的标杆,现测量者从E处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20m,FD=4m,EF=1.8m,求树AB的高度.
PAGE
第1/5页
