同步导学案28.1锐角三角函数3学案(无答案)
文档属性
| 名称 | 同步导学案28.1锐角三角函数3学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:43 | ||
图片预览

文档简介
学习课题:《28.1锐角三角函数(3)特殊角三角函数值》学习目标:1.能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数;2.能熟练计算含有30°、45°、60°角的三角函数的运算;3.能在实际问题中灵活运用. 重点:1.熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式难点:30°、45°、60°角的三角函数值的推导过程. 学习策略指导:让学生经历观察、操作等过程,知道特殊三角函数值,从事锐角三角函数基本性质的探索活动,进一步发展空间观察,增强审美意识. 【补充思考】
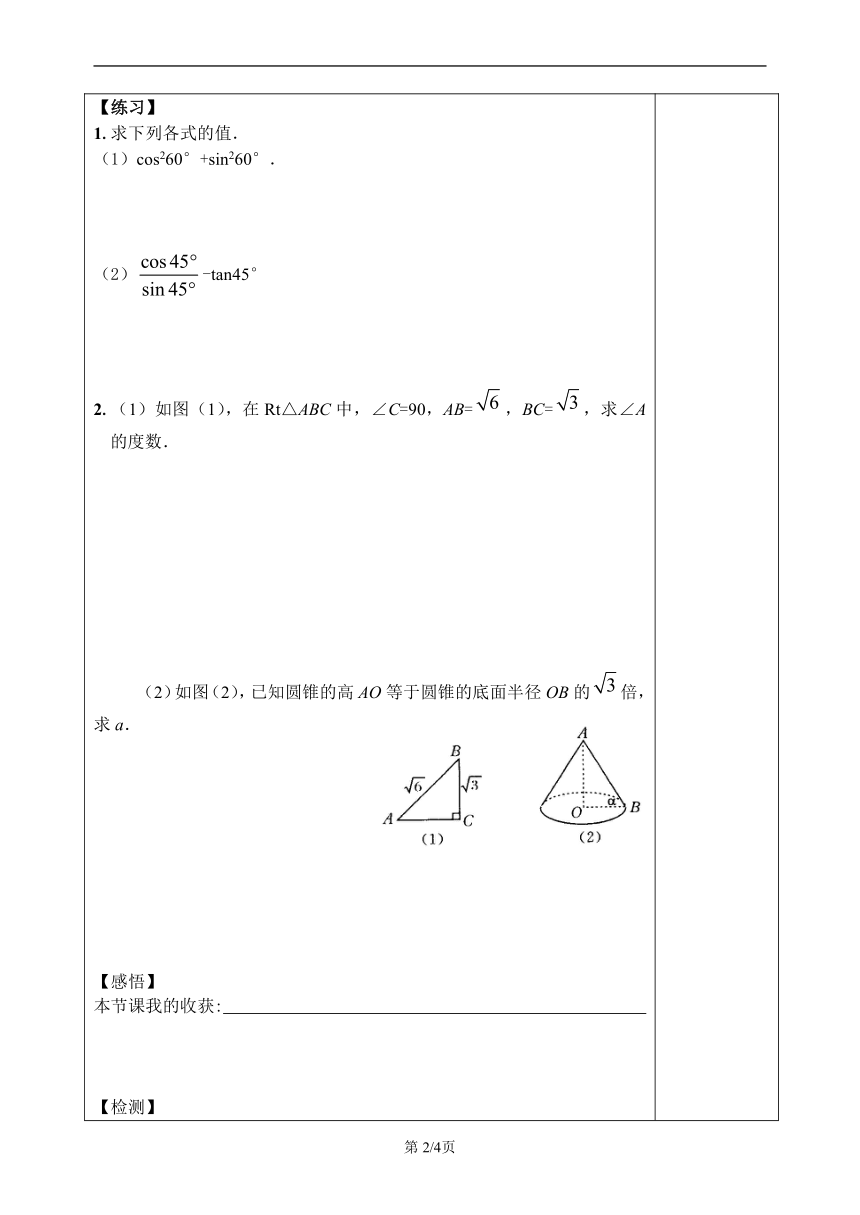
【回顾】一个直角三角形中,正弦的定义: 余弦的定义: 正切的定义: 【导入】 两块三角尺中含有几种不同的锐角? 分别是多少度? 【探究】请分别求出这几个锐角的正弦值、余弦值和正切值.过程:归纳结果:30°45°60°sinAcosAtanA【练习】1.求下列各式的值.cos260°+sin260°. -tan45°2.(1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数. (2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,求a.【感悟】本节课我的收获: 【检测】1.下列各式中不正确的是( ). A.sin260°+cos260°=1 B.sin30°+cos30°=1 C.sin35°=cos55° D.tan45°>sin45°2.计算2sin30°-2cos60°+tan45°的结果是( ). A.2 B. C. D.13.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB= eq \f(,2) ,则△ABC的形状是( )A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定4.计算:5.计算:【作业】A组1.sin60°的倒数为( )A.2 B. C. D.2.计算2sin30°﹣2cos60°+tan45°的结果是( )A.2 B. C. D.13.sin30°+cos60°= ,tan45°+cos60°= .4.在Rt△ABC中,∠C=90°,如果tanA=,那么cosB= .5.计算:2cos30°﹣﹣()﹣2= .B组6.求满足下列条件的锐角x:(1)cosx=(2)tanx﹣3=07.计算:2cos45°tan30°cos30°+sin260°.8.计算:﹣cot45°. 【补充思考】
PAGE
第4/4页
【回顾】一个直角三角形中,正弦的定义: 余弦的定义: 正切的定义: 【导入】 两块三角尺中含有几种不同的锐角? 分别是多少度? 【探究】请分别求出这几个锐角的正弦值、余弦值和正切值.过程:归纳结果:30°45°60°sinAcosAtanA【练习】1.求下列各式的值.cos260°+sin260°. -tan45°2.(1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数. (2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,求a.【感悟】本节课我的收获: 【检测】1.下列各式中不正确的是( ). A.sin260°+cos260°=1 B.sin30°+cos30°=1 C.sin35°=cos55° D.tan45°>sin45°2.计算2sin30°-2cos60°+tan45°的结果是( ). A.2 B. C. D.13.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB= eq \f(,2) ,则△ABC的形状是( )A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定4.计算:5.计算:【作业】A组1.sin60°的倒数为( )A.2 B. C. D.2.计算2sin30°﹣2cos60°+tan45°的结果是( )A.2 B. C. D.13.sin30°+cos60°= ,tan45°+cos60°= .4.在Rt△ABC中,∠C=90°,如果tanA=,那么cosB= .5.计算:2cos30°﹣﹣()﹣2= .B组6.求满足下列条件的锐角x:(1)cosx=(2)tanx﹣3=07.计算:2cos45°tan30°cos30°+sin260°.8.计算:﹣cot45°. 【补充思考】
PAGE
第4/4页
