同步导学案28.2.2应用举例---测量楼高(无答案)
文档属性
| 名称 | 同步导学案28.2.2应用举例---测量楼高(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:43 | ||
图片预览


文档简介
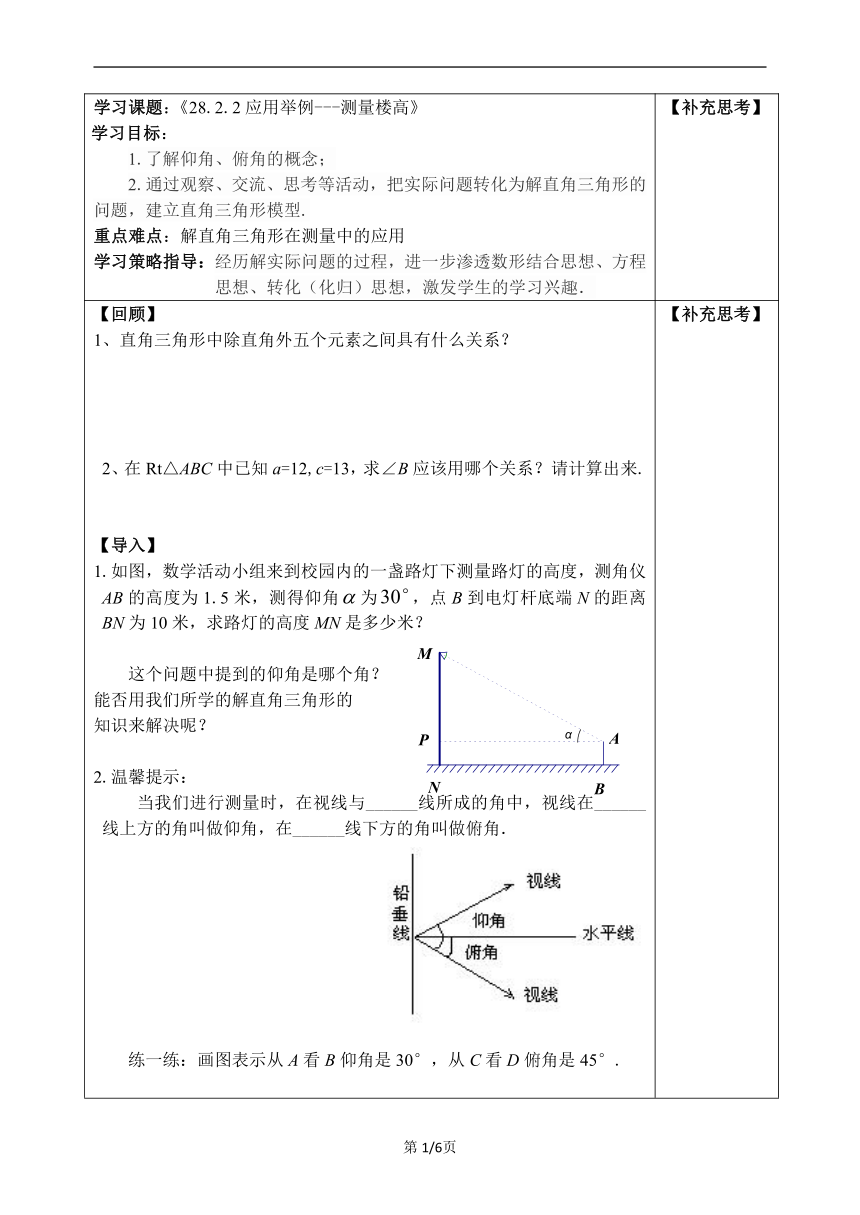
学习课题:《28.2.2应用举例---测量楼高》学习目标:1.了解仰角、俯角的概念;2.通过观察、交流、思考等活动,把实际问题转化为解直角三角形的问题,建立直角三角形模型.重点难点:解直角三角形在测量中的应用学习策略指导:经历解实际问题的过程,进一步渗透数形结合思想、方程思想、转化(化归)思想,激发学生的学习兴趣. 【补充思考】
【回顾】1、直角三角形中除直角外五个元素之间具有什么关系? 2、在Rt△ABC中已知a=12,c=13,求∠B应该用哪个关系?请计算出来.【导入】1.如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪AB的高度为1.5米,测得仰角为,点B到电灯杆底端N的距离BN为10米,求路灯的高度MN是多少米?这个问题中提到的仰角是哪个角?能否用我们所学的解直角三角形的知识来解决呢?2.温馨提示: 当我们进行测量时,在视线与______线所成的角中,视线在______线上方的角叫做仰角,在______线下方的角叫做俯角. 练一练:画图表示从A看B仰角是30°,从C看D俯角是45°.【探究】铺垫练习 飞机于空中A处探测到地面目标B,此时从飞机上看目标B俯角α=30°,飞行高度AC是1200米,求此时飞机到目标B的距离.热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m.这栋楼有多高(结果取整数) 【补充思考】
【练习】1.如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪AB的高度为1.5米,测得仰角为,点B到电灯杆底端N的距离BN为10米,求路灯的高度MN是多少米? 2.建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m). (sin54°=0.8090,cos54°=0.5878,tan54°=1.376)【感悟】1.知识归纳:2.数学思想方法:3.学习体会:【检测】1.如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC= 米.2.如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米. 第1题 第2题【作业】A组1.如果从某一高处甲看低处乙的俯角为30°,那么从乙处看甲处,甲在乙的( )A.俯角30°方向 B.俯角60°方向 C.仰角30°方向 D.仰角60°方向2.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )A.200米 B.200米 C.220米 D.米三.解答题(共3小题)3.如图,AB,CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,求建筑物CD的高度.4.如图,小明利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为60米,且AB垂直于桥面.(点A,B,C,M在同一平面内)(1)求大桥主架在桥面以上的高度AM;(结果保留根号)(2)求大桥主架在水面以上的高度AB.(结果精确到1米)(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,≈1.73)5.如图,小明想用所学的知识来测量长安塔的高度,他先在E处用侧倾器测得塔顶A的仰角α为30°,然后,他从E处迎着塔的方向走了71.1米到F处,再用侧倾器测得塔顶A的仰角β为45°,已知点E、F、B在同一水平面上,侧倾器的高度为1.6米,请你利用小明测得的相关数据,求长安塔的高度AB(结果精确到1米.参考数据:≈1.41,≈1.73) 【补充思考】
C
B
A
C
B
A
PAGE
第2/6页
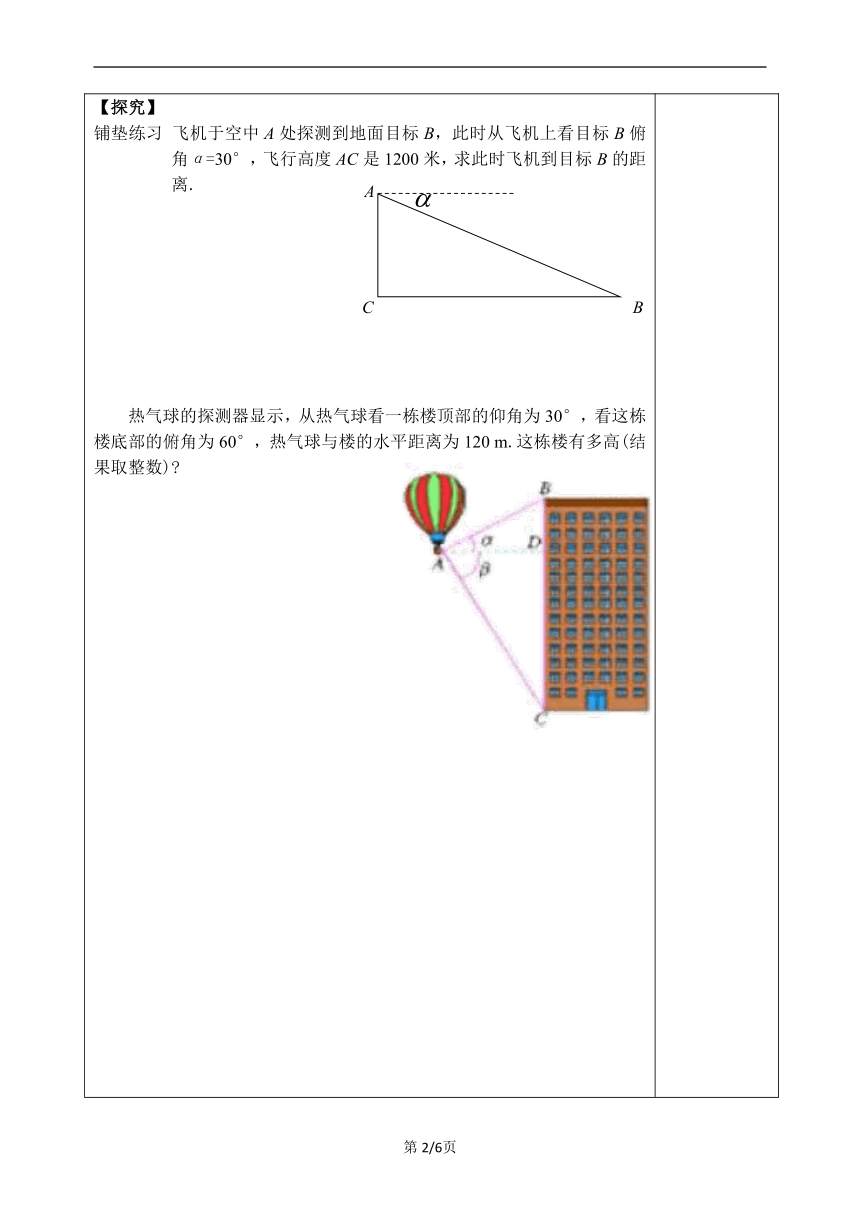
【回顾】1、直角三角形中除直角外五个元素之间具有什么关系? 2、在Rt△ABC中已知a=12,c=13,求∠B应该用哪个关系?请计算出来.【导入】1.如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪AB的高度为1.5米,测得仰角为,点B到电灯杆底端N的距离BN为10米,求路灯的高度MN是多少米?这个问题中提到的仰角是哪个角?能否用我们所学的解直角三角形的知识来解决呢?2.温馨提示: 当我们进行测量时,在视线与______线所成的角中,视线在______线上方的角叫做仰角,在______线下方的角叫做俯角. 练一练:画图表示从A看B仰角是30°,从C看D俯角是45°.【探究】铺垫练习 飞机于空中A处探测到地面目标B,此时从飞机上看目标B俯角α=30°,飞行高度AC是1200米,求此时飞机到目标B的距离.热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m.这栋楼有多高(结果取整数) 【补充思考】
【练习】1.如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪AB的高度为1.5米,测得仰角为,点B到电灯杆底端N的距离BN为10米,求路灯的高度MN是多少米? 2.建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m). (sin54°=0.8090,cos54°=0.5878,tan54°=1.376)【感悟】1.知识归纳:2.数学思想方法:3.学习体会:【检测】1.如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC= 米.2.如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米. 第1题 第2题【作业】A组1.如果从某一高处甲看低处乙的俯角为30°,那么从乙处看甲处,甲在乙的( )A.俯角30°方向 B.俯角60°方向 C.仰角30°方向 D.仰角60°方向2.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )A.200米 B.200米 C.220米 D.米三.解答题(共3小题)3.如图,AB,CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,求建筑物CD的高度.4.如图,小明利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为60米,且AB垂直于桥面.(点A,B,C,M在同一平面内)(1)求大桥主架在桥面以上的高度AM;(结果保留根号)(2)求大桥主架在水面以上的高度AB.(结果精确到1米)(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,≈1.73)5.如图,小明想用所学的知识来测量长安塔的高度,他先在E处用侧倾器测得塔顶A的仰角α为30°,然后,他从E处迎着塔的方向走了71.1米到F处,再用侧倾器测得塔顶A的仰角β为45°,已知点E、F、B在同一水平面上,侧倾器的高度为1.6米,请你利用小明测得的相关数据,求长安塔的高度AB(结果精确到1米.参考数据:≈1.41,≈1.73) 【补充思考】
C
B
A
C
B
A
PAGE
第2/6页
