同步导学案28.2.2应用举例---方向角问题(无答案)
文档属性
| 名称 | 同步导学案28.2.2应用举例---方向角问题(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 357.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:43 | ||
图片预览

文档简介
学习课题:《28.2.2应用举例---方向角问题》学习目标:1.了解方向角的概念,能画图表示所指的方向角是哪一个角;2.逐步培养分析问题、解决问题的能力;体会数形结合的数学思想和方法;3.会用解直角三角形有关知识解决方向角问题.重难点:学会准确分析问题并将实际问题转化成数学模型学习策略指导:结合地图知识掌握方位角,实现知识跨学科融合. 【补充思考】
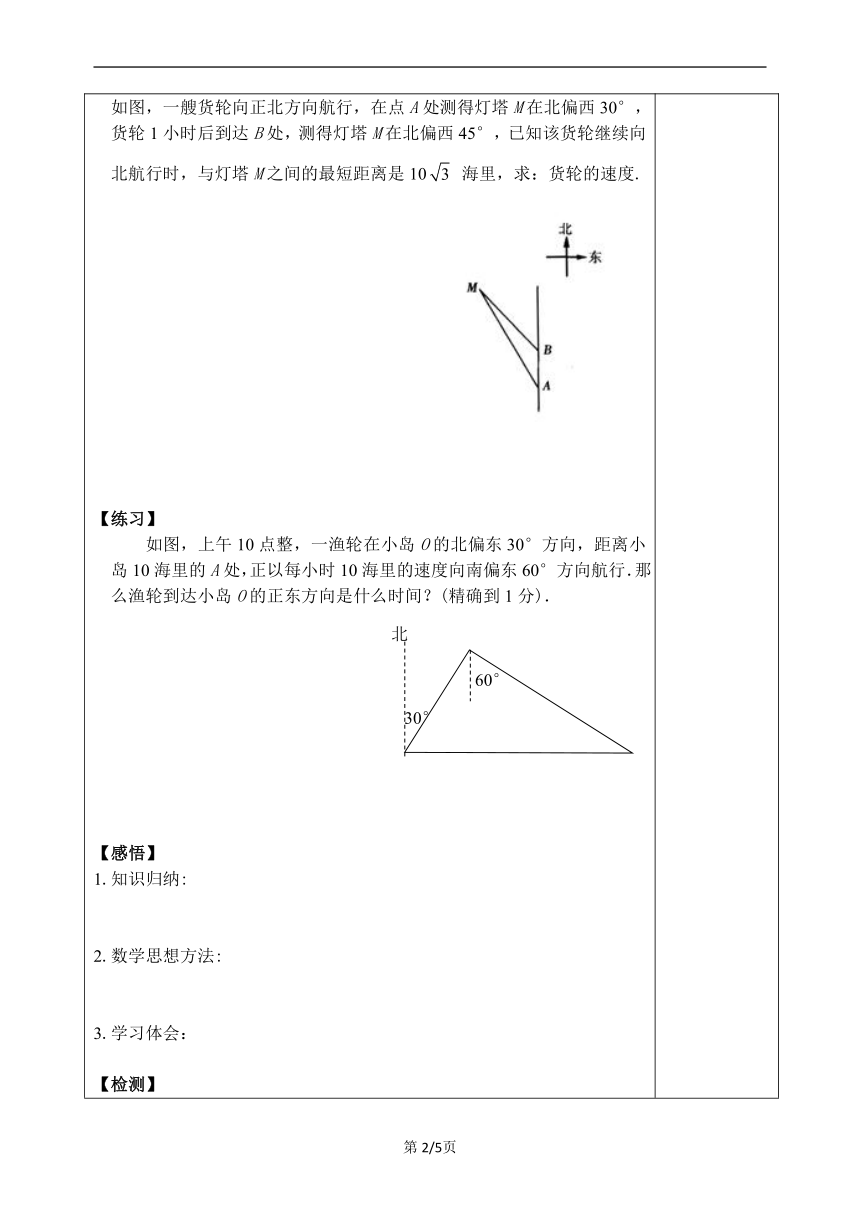
【导入】方向角的概念:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度。1.画出方向图(表示东南西北四个方向的).2.依次画出表示东南方向、西北方向、北偏东65°、南偏东34°方向的射线.【探究】例 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,B处距离灯塔P有多远(结果取整数) 补例:如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮1小时后到达B处,测得灯塔M在北偏西45°,已知该货轮继续向北航行时,与灯塔M之间的最短距离是10 海里,求:货轮的速度.【练习】如图,上午10点整,一渔轮在小岛O的北偏东30°方向,距离小岛10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分). 【感悟】1.知识归纳:2.数学思想方法:3.学习体会:【检测】1. 一个人从A点出发向北偏东60°方向走了一段距离到达B点,再从B点出发向南偏东15°方向走了一段距离到C点,则∠ABC的度数为 ( )A.15° B.75° C.105° D.45°2.如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点 A,以 A为圆心、500 m为半径的圆形区域为居民区.取MN 上 另一点B,测得BA的方向为南偏东 75°.已知MB=400 m,通过计算回答,如果不改变方向,输水路线是否会穿过居民区?【作业】A组1.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )A.100m B.100m C.100m D.m2.如图,点P在点A的北偏东60°方向上,点B在点A正东方向,点P在点B的北偏东30°方向上,若AB=50米,则点P到直线AB的距离为( )A.50米 B.25米 C.50米 D.25米3.如图,某海岸边有B,C两码头,C码头位于B码头的正东方向,距B码头40海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东30°方向的C码头航行,当甲船到达距B码头30海里的E处时,乙船位于甲船北偏东60°方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)B组4.如图,C处是一钻井平台,位于东营港口A的北偏东60°方向上,与港口A相距60海里,一艘摩托艇从A出发,自西向东航行至B时,改变航向以每小时50海里的速度沿BC方向行进,此时C位于B的北偏西45°方向,则从B到达C需要多少小时?5.A,B两地间有一段笔直的高速铁路,长度为100km.某时发生的地震对地面上以点C为圆心,30km为半径的圆形区域内的建筑物有影响.分别从A,B两地处测得点C的方位角如图所示,tanα=1.776,tanβ=1.224.高速铁路是否会受到地震的影响?请通过计算说明理由.
北
30°
60°
PAGE
第5/5页
【导入】方向角的概念:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度。1.画出方向图(表示东南西北四个方向的).2.依次画出表示东南方向、西北方向、北偏东65°、南偏东34°方向的射线.【探究】例 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,B处距离灯塔P有多远(结果取整数) 补例:如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮1小时后到达B处,测得灯塔M在北偏西45°,已知该货轮继续向北航行时,与灯塔M之间的最短距离是10 海里,求:货轮的速度.【练习】如图,上午10点整,一渔轮在小岛O的北偏东30°方向,距离小岛10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分). 【感悟】1.知识归纳:2.数学思想方法:3.学习体会:【检测】1. 一个人从A点出发向北偏东60°方向走了一段距离到达B点,再从B点出发向南偏东15°方向走了一段距离到C点,则∠ABC的度数为 ( )A.15° B.75° C.105° D.45°2.如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点 A,以 A为圆心、500 m为半径的圆形区域为居民区.取MN 上 另一点B,测得BA的方向为南偏东 75°.已知MB=400 m,通过计算回答,如果不改变方向,输水路线是否会穿过居民区?【作业】A组1.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )A.100m B.100m C.100m D.m2.如图,点P在点A的北偏东60°方向上,点B在点A正东方向,点P在点B的北偏东30°方向上,若AB=50米,则点P到直线AB的距离为( )A.50米 B.25米 C.50米 D.25米3.如图,某海岸边有B,C两码头,C码头位于B码头的正东方向,距B码头40海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东30°方向的C码头航行,当甲船到达距B码头30海里的E处时,乙船位于甲船北偏东60°方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)B组4.如图,C处是一钻井平台,位于东营港口A的北偏东60°方向上,与港口A相距60海里,一艘摩托艇从A出发,自西向东航行至B时,改变航向以每小时50海里的速度沿BC方向行进,此时C位于B的北偏西45°方向,则从B到达C需要多少小时?5.A,B两地间有一段笔直的高速铁路,长度为100km.某时发生的地震对地面上以点C为圆心,30km为半径的圆形区域内的建筑物有影响.分别从A,B两地处测得点C的方位角如图所示,tanα=1.776,tanβ=1.224.高速铁路是否会受到地震的影响?请通过计算说明理由.
北
30°
60°
PAGE
第5/5页
