同步导学案28.2.2应用举例---坡度与坡角(无答案)
文档属性
| 名称 | 同步导学案28.2.2应用举例---坡度与坡角(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 968.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:54:43 | ||
图片预览


文档简介
学习课题:《28.2.2解直角三角形在测量中的应用》学习目标:1.了解坡度、坡角的概念;2.通过观察、交流、思考等活动,把实际问题中坡度、坡角问题转化为解直角三角形的问题,建立直角三角形模型;
3.经历解实际问题的过程,进一步渗透数形结合思想、方程思想、转化(化归)思想,激发学生的学习兴趣.重难点:坡度、坡角在实际问题中的应用.学习策略指导:结合图形独立理解概念并运用到实际问题当中. 【补充思考】
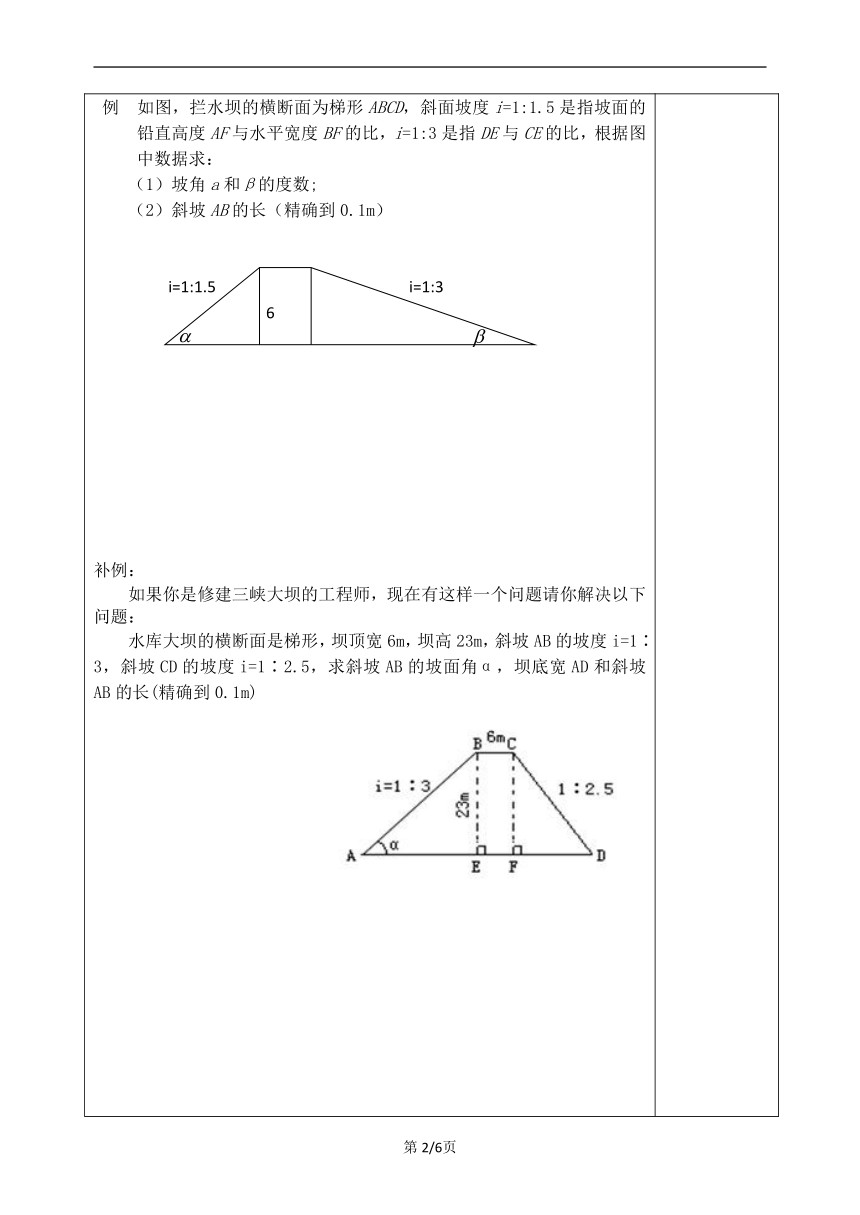
【回顾】 利用解直角三角形的知识解决实际问题的一般过程【导入】1. 坡度与坡角坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),一般用i表示。即i=,常写成i=1:m的形式如i=1:2.5, 把坡面与水平面的夹角α叫做坡角.2.结合图形思考,坡度i与坡角α之间具有什么关系? 【探究】铺垫练习(1)一段坡面的坡角为60°,则坡度i=______;已知一段坡面的铅直高度为,坡面长为,则坡度i=______,坡角______度例 如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,i=1:3是指DE与CE的比,根据图中数据求:(1)坡角a和β的度数;(2)斜坡AB的长(精确到0.1m) 补例:如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决以下问题:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m) 【补充思考】
【练习】1.一只船向正东航行,上午7时在灯塔A的正北C处,上午9时到达塔的北偏东60°的B处,已知船的速度为每小时20千米,那么AB的距离是( )千米.A. B. C. D. 2.测得某坡面垂直高度为2m,水平宽度为4m,则坡度为 ( )A. B. C.2:1 D.1:23.如图:已知在一峭壁顶点B测得地面上一点A俯角60°,竖直下降10米至D,测得A点俯角45°,那么峭壁的高BC是___________米(精确到0.1米)4. 如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上相邻两树的坡面距离是多少(精确到0.1m).【感悟】1.知识归纳:2.数学思想方法:3.学习体会:【检测】如图:铁路的路基的横截面是等腰梯形,斜坡AB的坡度为1∶,BE为3米,求路基的高AE及坡角B的度数.【作业】A组1.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )A.10tan36° B.10cos36° C.10sin36° D.2.如图,一个小球沿倾斜角为α的斜坡向下滚动,经过5秒时,测得小球的平均速度为0.5米/秒.已知cosα=,则小球下降的高度是( )A.1米 B.1.5米 C.2米 D.2.5米3.如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB的水平宽度AC为12米,则斜坡AB的长为( )A.4米 B.6米 C.6米 D.24米4.如图所示,河堤横断面迎水坡AB的坡度是1:2,堤高BC=4m,则坡面AB的长度是( )A.8m B.16m C.4m D.4mB组5.淮安华联商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为45°,改造后的斜坡式自动扶梯的坡角∠ACB为15°,改造后的斜坡式自动扶梯水平距离增加了BC,请你计算BC的长度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.41)6.如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α要满足60°≤α≤75°,现有一架长5.5m的梯子.(1)使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?(2)当梯子底端距离墙面2.2m时,α等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,sin23.6°≈0.40,cos66.4°≈0.40,tan21.8°≈0.40.) 【补充思考】
i=1:1.5
i=1:3
6
PAGE
第1/6页
3.经历解实际问题的过程,进一步渗透数形结合思想、方程思想、转化(化归)思想,激发学生的学习兴趣.重难点:坡度、坡角在实际问题中的应用.学习策略指导:结合图形独立理解概念并运用到实际问题当中. 【补充思考】
【回顾】 利用解直角三角形的知识解决实际问题的一般过程【导入】1. 坡度与坡角坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),一般用i表示。即i=,常写成i=1:m的形式如i=1:2.5, 把坡面与水平面的夹角α叫做坡角.2.结合图形思考,坡度i与坡角α之间具有什么关系? 【探究】铺垫练习(1)一段坡面的坡角为60°,则坡度i=______;已知一段坡面的铅直高度为,坡面长为,则坡度i=______,坡角______度例 如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,i=1:3是指DE与CE的比,根据图中数据求:(1)坡角a和β的度数;(2)斜坡AB的长(精确到0.1m) 补例:如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决以下问题:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m) 【补充思考】
【练习】1.一只船向正东航行,上午7时在灯塔A的正北C处,上午9时到达塔的北偏东60°的B处,已知船的速度为每小时20千米,那么AB的距离是( )千米.A. B. C. D. 2.测得某坡面垂直高度为2m,水平宽度为4m,则坡度为 ( )A. B. C.2:1 D.1:23.如图:已知在一峭壁顶点B测得地面上一点A俯角60°,竖直下降10米至D,测得A点俯角45°,那么峭壁的高BC是___________米(精确到0.1米)4. 如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上相邻两树的坡面距离是多少(精确到0.1m).【感悟】1.知识归纳:2.数学思想方法:3.学习体会:【检测】如图:铁路的路基的横截面是等腰梯形,斜坡AB的坡度为1∶,BE为3米,求路基的高AE及坡角B的度数.【作业】A组1.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )A.10tan36° B.10cos36° C.10sin36° D.2.如图,一个小球沿倾斜角为α的斜坡向下滚动,经过5秒时,测得小球的平均速度为0.5米/秒.已知cosα=,则小球下降的高度是( )A.1米 B.1.5米 C.2米 D.2.5米3.如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB的水平宽度AC为12米,则斜坡AB的长为( )A.4米 B.6米 C.6米 D.24米4.如图所示,河堤横断面迎水坡AB的坡度是1:2,堤高BC=4m,则坡面AB的长度是( )A.8m B.16m C.4m D.4mB组5.淮安华联商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为45°,改造后的斜坡式自动扶梯的坡角∠ACB为15°,改造后的斜坡式自动扶梯水平距离增加了BC,请你计算BC的长度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.41)6.如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α要满足60°≤α≤75°,现有一架长5.5m的梯子.(1)使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?(2)当梯子底端距离墙面2.2m时,α等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,sin23.6°≈0.40,cos66.4°≈0.40,tan21.8°≈0.40.) 【补充思考】
i=1:1.5
i=1:3
6
PAGE
第1/6页
