同步导学案29.2.1三视图第1课时(无答案)
文档属性
| 名称 | 同步导学案29.2.1三视图第1课时(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:57:33 | ||
图片预览

文档简介
学习课题:《 29.2.1 三视图》学习目标:1.记住主视图,俯视图,左视图的概念2.会画简单几何体的三视图重点知识:画简单的三视图难点问题:画出三棱柱的三视图学习策略指导:通过观察、动手画图、思考等学习方式学习,学会总结、善于总结. 【补充思考】
【回顾】中心投影___________________平行投影____________________正投影 _______________【导入】当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.单一的视图通常只能反映物体一个方面的形状.为了全面反映物体的形状,生产实践中往往采用多个视图来反映同一物体不同方面的形状.本章中我们只讨论三视图.【探究】自主探索1:1)三视图指什么? 主视图是指 左视图是指 俯视图是指 2)三视图中各视图的大小有何关系 自主探索2:常见几何体的三视图例1 画出图29.2-4中基本几何体的三视图.圆柱(1) 正三棱柱(2) 球(3)分析:画这些基本几何体的三视图时,要注意从三个方面观察它们.具体画法为: 1.确定主视图的位置,画出主视图; 2.在主视图正下方画出俯视图,注意与主视图“长对正”.3.在主视图正右方画出左视图.注意与主视图“高平齐”,与俯视图“宽相等”.4.为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线( )表示对称轴. 【补充思考】
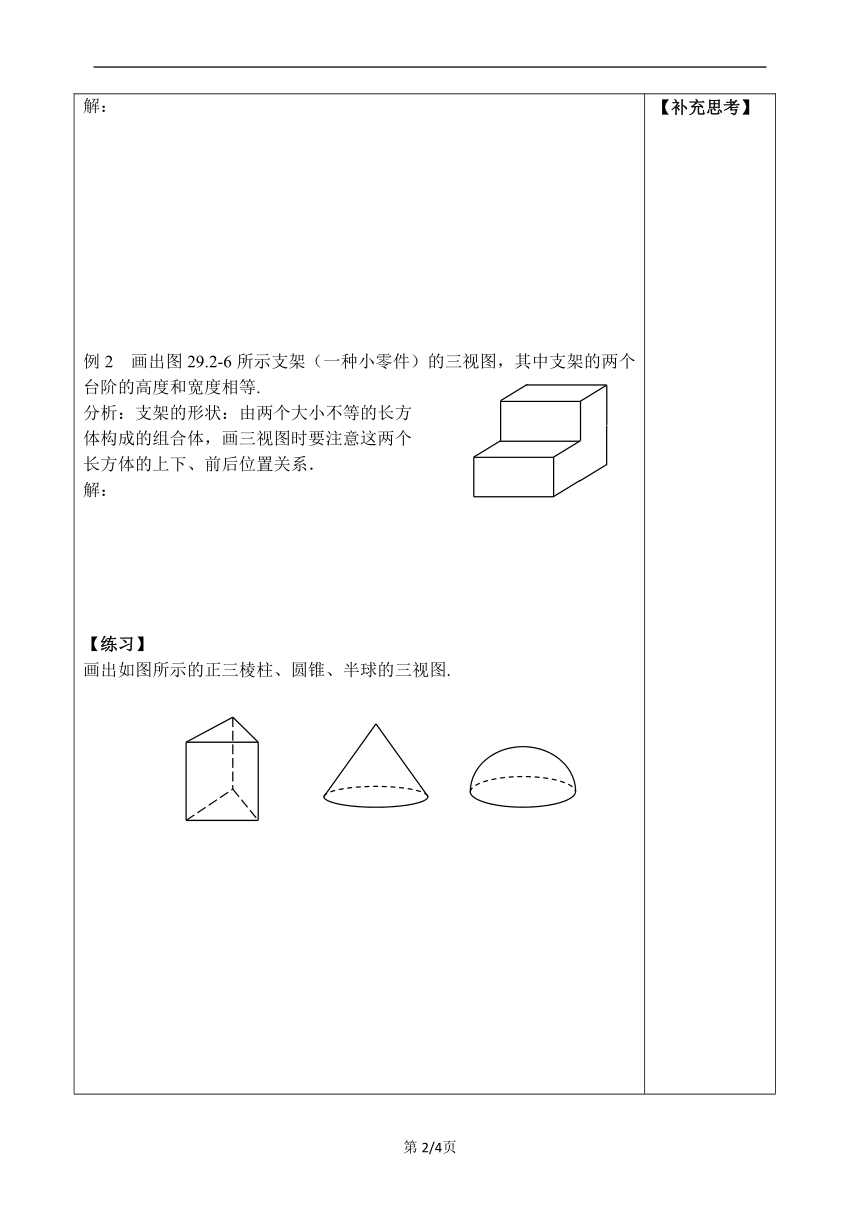
解:例2 画出图29.2-6所示支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.分析:支架的形状:由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长方体的上下、前后位置关系. 解:【练习】画出如图所示的正三棱柱、圆锥、半球的三视图. 【补充思考】
【感悟】这节课你有哪些收获,请在这里写一写.通过本节课的学习,我学到了...本节知识框图结构:我还有以下困惑... 【补充思考】
【检测】1.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.2.画出图中几何体的三视图.【作业】A组1.如图所示的几何体的主视图为( ) A. B. C. D.2.下列几何体中,俯视图为三角形的是( )A. B. C. D.3.下面四个几何体中,左视图为圆的是( )A. B. C. D.4.如图所示,该几何体的俯视图是( )A.B. C. D.5.分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )A.圆锥 B.圆柱 C.三棱柱D.正方体B组6.如图中的几何体是由六个完全相同的小正方体组成的,它的主视图是( )A. B.C.D.7.如图,一个由圆柱和长方体组成的几何体水平放置,它的俯视图是( ) A. B. C. D.8.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )A. B. C. D.9.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )A.主视图改变,左视图改变 B.俯视图不变,左视图不变 C.俯视图改变,左视图改变 D.主视图改变,左视图不变10.将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )A.B.C. D.
PAGE
第2/4页
【回顾】中心投影___________________平行投影____________________正投影 _______________【导入】当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.单一的视图通常只能反映物体一个方面的形状.为了全面反映物体的形状,生产实践中往往采用多个视图来反映同一物体不同方面的形状.本章中我们只讨论三视图.【探究】自主探索1:1)三视图指什么? 主视图是指 左视图是指 俯视图是指 2)三视图中各视图的大小有何关系 自主探索2:常见几何体的三视图例1 画出图29.2-4中基本几何体的三视图.圆柱(1) 正三棱柱(2) 球(3)分析:画这些基本几何体的三视图时,要注意从三个方面观察它们.具体画法为: 1.确定主视图的位置,画出主视图; 2.在主视图正下方画出俯视图,注意与主视图“长对正”.3.在主视图正右方画出左视图.注意与主视图“高平齐”,与俯视图“宽相等”.4.为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线( )表示对称轴. 【补充思考】
解:例2 画出图29.2-6所示支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.分析:支架的形状:由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长方体的上下、前后位置关系. 解:【练习】画出如图所示的正三棱柱、圆锥、半球的三视图. 【补充思考】
【感悟】这节课你有哪些收获,请在这里写一写.通过本节课的学习,我学到了...本节知识框图结构:我还有以下困惑... 【补充思考】
【检测】1.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.2.画出图中几何体的三视图.【作业】A组1.如图所示的几何体的主视图为( ) A. B. C. D.2.下列几何体中,俯视图为三角形的是( )A. B. C. D.3.下面四个几何体中,左视图为圆的是( )A. B. C. D.4.如图所示,该几何体的俯视图是( )A.B. C. D.5.分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )A.圆锥 B.圆柱 C.三棱柱D.正方体B组6.如图中的几何体是由六个完全相同的小正方体组成的,它的主视图是( )A. B.C.D.7.如图,一个由圆柱和长方体组成的几何体水平放置,它的俯视图是( ) A. B. C. D.8.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )A. B. C. D.9.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )A.主视图改变,左视图改变 B.俯视图不变,左视图不变 C.俯视图改变,左视图改变 D.主视图改变,左视图不变10.将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )A.B.C. D.
PAGE
第2/4页
