同步导学案29.2.2三视图第2课时(无答案)
文档属性
| 名称 | 同步导学案29.2.2三视图第2课时(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 143.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:57:33 | ||
图片预览

文档简介
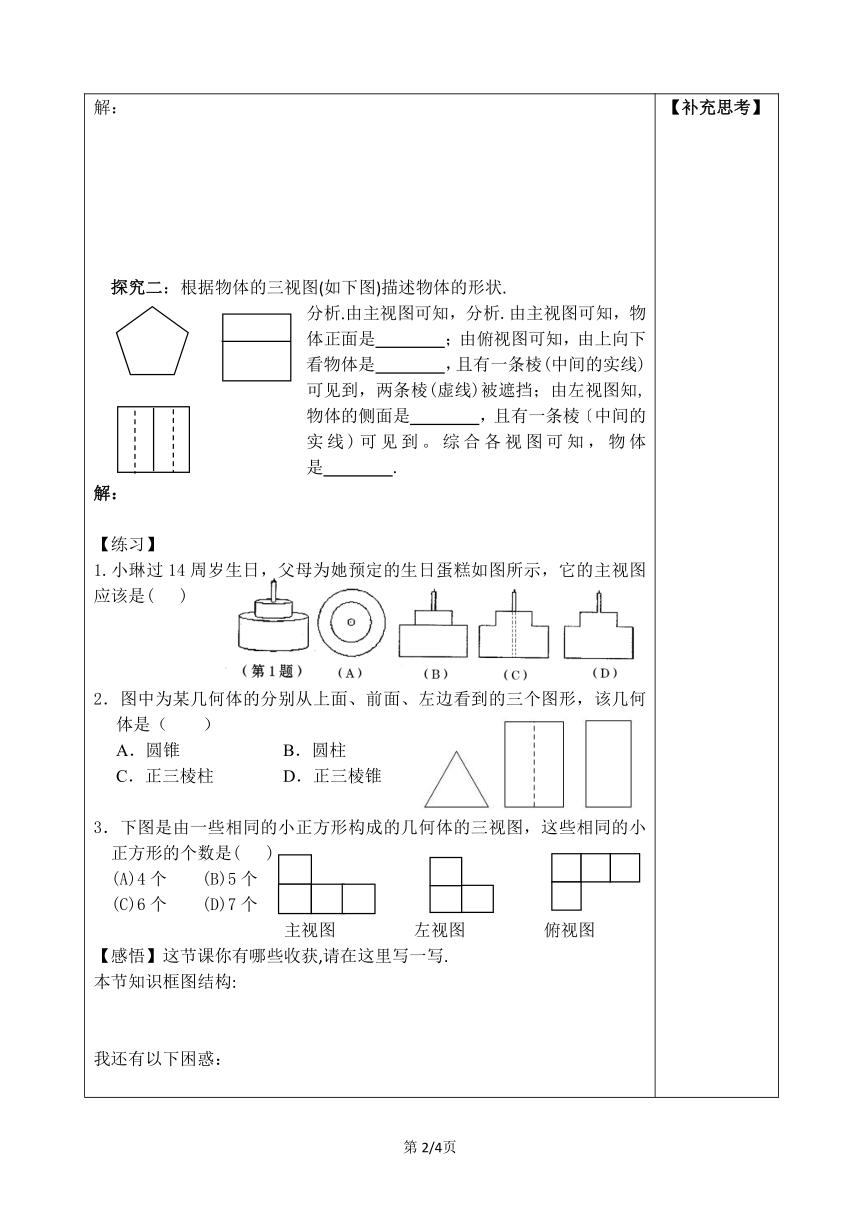
学习课题: 《 29.2.2 三视图》学习目标:1.会根据物体的三视图描述出几何体的基本形状或实物原型;2.让我们经历探索简单几何体三视图的还原,进一步发展空间想象能力;3.学会关注生活中有关投影的数学问题,提高数学的应用意识.重点知识:根据物体的三视图描述出几何体的基本形状或实物原型难点问题: 根据物体的三视图描述出几何体的基本形状或实物原型学习策略指导:引导学生通过观察、动手画图、思考等学习方式学习,指导学生学会总结、善于总结. 【补充思考】
【回顾】1. 画出右图中基本几何体的三视图.2.某几何体的三视图如右图所示,则该几何体是( )A.长方体 B.圆锥 C.圆柱 D.球【导入】我们会由立体图形(实物)画出三视图,那么由三视图能否也想象出立体图形(实物)呢? 【探究】探究一:根据下面的三视图说出立体图形的名称. 分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形,(1)由主视图可知,物体正面是 ;由俯视图可知,由上向下看物体是 ;由左视图知,物体的侧面是 .综合各视图可知,物体是 .(2)由主视图可知,物体正面是 ;由俯视图可知,由上向下看物体是 ;由左视图知,物体的侧面是 .综合各视图可知,物体是 【补充思考】
解:探究二:根据物体的三视图(如下图)描述物体的形状.分析.由主视图可知,分析.由主视图可知,物体正面是 ;由俯视图可知,由上向下看物体是 ,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图知,物体的侧面是 ,且有一条棱〔中间的实线)可见到。综合各视图可知,物体是 .解:【练习】 1.小琳过14周岁生日,父母为她预定的生日蛋糕如图所示,它的主视图应该是( )2.图中为某几何体的分别从上面、前面、左边看到的三个图形,该几何体是( )A.圆锥 B.圆柱 C.正三棱柱 D.正三棱锥3.下图是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( ) (A)4个 (B)5个 (C)6个 (D)7个 主视图 左视图 俯视图【感悟】这节课你有哪些收获,请在这里写一写.本节知识框图结构:我还有以下困惑: 【补充思考】
【检测】1.两个物体的主视图都是圆,则这两个物体可能是( ) (A)圆柱体、圆锥体 (B)圆柱体、正方体 (C)圆柱体、球 (D)圆锥体、球2.一个物体的俯视图是圆,则该物体有可能是 (写两个即可).3.一个几何体的三视图如图所示,则这个几何体的名称是 .4.如图,是一个几何体的三视图,则这个几何体是( )A.B. C. D.【作业】A组1.若一个几何体的主视图、左视图、俯视图都是正方形,则这个几何体是( )A.圆柱 B.圆锥 C.正方体 D.球2.如图所示的主视图对应的几何体是( ) A. B. C. D.3.下面是一些立体图形的三视图(如图),请在括号内填上立体图形的名称.4.已知某物体的三视图如图所示,那么与它对应的物体是( )A. B.C. D.4.诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图是对某物体从不同角度观察的记录情况,对该物体判断最接近本质的是( )A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管 B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管 C.是圆柱形物体,里面有两个垂直的空心管 D.是圆柱形物体,里面有两个平行的空心管B组5.如图分别是某校体育运动会的颁奖台和它的主视图,则其左视图是( )A. B. C. D.6.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.7.桌上摆着一个由若干个相同小正方体组成的几何体,其三视图如图所示,则组成此几何体需要的小正方体的个数是( )A.5 B.6 C.7 D.88.一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )A.4 B.5 C.6 D.7
主视图
俯视图
左视图
PAGE
第4/4页
【回顾】1. 画出右图中基本几何体的三视图.2.某几何体的三视图如右图所示,则该几何体是( )A.长方体 B.圆锥 C.圆柱 D.球【导入】我们会由立体图形(实物)画出三视图,那么由三视图能否也想象出立体图形(实物)呢? 【探究】探究一:根据下面的三视图说出立体图形的名称. 分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形,(1)由主视图可知,物体正面是 ;由俯视图可知,由上向下看物体是 ;由左视图知,物体的侧面是 .综合各视图可知,物体是 .(2)由主视图可知,物体正面是 ;由俯视图可知,由上向下看物体是 ;由左视图知,物体的侧面是 .综合各视图可知,物体是 【补充思考】
解:探究二:根据物体的三视图(如下图)描述物体的形状.分析.由主视图可知,分析.由主视图可知,物体正面是 ;由俯视图可知,由上向下看物体是 ,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图知,物体的侧面是 ,且有一条棱〔中间的实线)可见到。综合各视图可知,物体是 .解:【练习】 1.小琳过14周岁生日,父母为她预定的生日蛋糕如图所示,它的主视图应该是( )2.图中为某几何体的分别从上面、前面、左边看到的三个图形,该几何体是( )A.圆锥 B.圆柱 C.正三棱柱 D.正三棱锥3.下图是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( ) (A)4个 (B)5个 (C)6个 (D)7个 主视图 左视图 俯视图【感悟】这节课你有哪些收获,请在这里写一写.本节知识框图结构:我还有以下困惑: 【补充思考】
【检测】1.两个物体的主视图都是圆,则这两个物体可能是( ) (A)圆柱体、圆锥体 (B)圆柱体、正方体 (C)圆柱体、球 (D)圆锥体、球2.一个物体的俯视图是圆,则该物体有可能是 (写两个即可).3.一个几何体的三视图如图所示,则这个几何体的名称是 .4.如图,是一个几何体的三视图,则这个几何体是( )A.B. C. D.【作业】A组1.若一个几何体的主视图、左视图、俯视图都是正方形,则这个几何体是( )A.圆柱 B.圆锥 C.正方体 D.球2.如图所示的主视图对应的几何体是( ) A. B. C. D.3.下面是一些立体图形的三视图(如图),请在括号内填上立体图形的名称.4.已知某物体的三视图如图所示,那么与它对应的物体是( )A. B.C. D.4.诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图是对某物体从不同角度观察的记录情况,对该物体判断最接近本质的是( )A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管 B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管 C.是圆柱形物体,里面有两个垂直的空心管 D.是圆柱形物体,里面有两个平行的空心管B组5.如图分别是某校体育运动会的颁奖台和它的主视图,则其左视图是( )A. B. C. D.6.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.7.桌上摆着一个由若干个相同小正方体组成的几何体,其三视图如图所示,则组成此几何体需要的小正方体的个数是( )A.5 B.6 C.7 D.88.一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )A.4 B.5 C.6 D.7
主视图
俯视图
左视图
PAGE
第4/4页
