同步导学案29.2.3三视图第3课时(无答案)
文档属性
| 名称 | 同步导学案29.2.3三视图第3课时(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 109.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 09:57:33 | ||
图片预览

文档简介
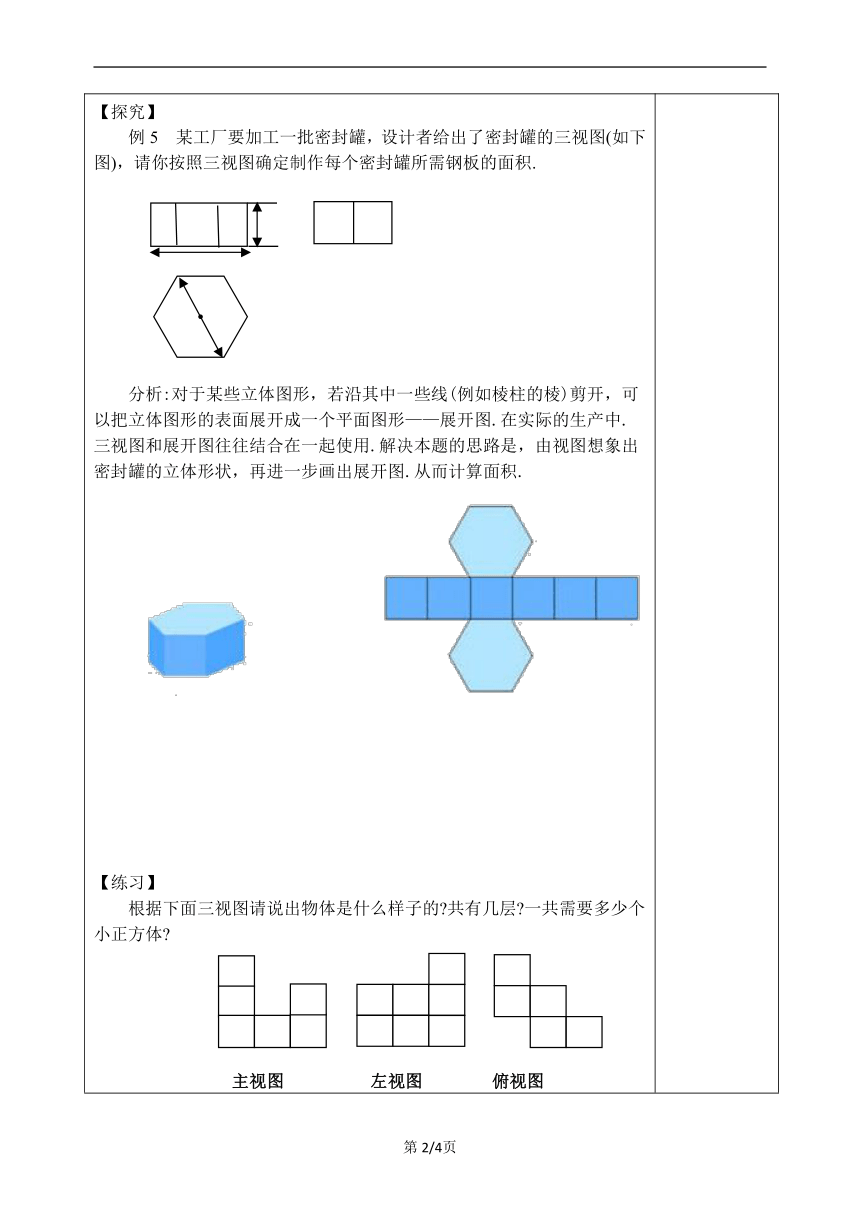
学习课题:《 29.2.3 三视图》学习目标:1.学会根据物体的三视图描述出几何体的基本形状或实物原型;2.经历探索简单的几何体的三视图的还原,进一步的发展空间想象能力;3.了解将三视图转换成立体图开在生产中的作用,并会计算几何体的表面积或体积.重点知识:根据三视图描述基本几何体和实物原型及三视图在生产中的作用.难点问题: 根据三视图想象基本几何体和实物原型的形状,并会求几何体的表面积或体积.学习策略指导:引导学生通过观察、动手画图、思考等学习方式学习,指导学生学会总结、善于总结.为高中的立体几何的学习,打下坚实的基础. 【补充思考】
【回顾】完成下列练习:(1)如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称____.(2)一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有_____个碟子.(3)某几何体的三种视图分别如下图所示,那么这个几何体可能是( ).(A)长方体 (B)圆柱 (C)圆锥 (D)球【导入】让学生欣赏事先准备好的机械制图中三视图与对应立体图形的图片,借助图片信息让学生体会到本章知识的价值.并借此可以讲述一下现在一些中专、中技甚至大学里开设的模具和机械制图专业和课程就需要这方面的知识,激发学生的学习兴趣,导入本课. 【补充思考】
【探究】例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请你按照三视图确定制作每个密封罐所需钢板的面积. 100 100分析:对于某些立体图形,若沿其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中.三视图和展开图往往结合在一起使用.解决本题的思路是,由视图想象出密封罐的立体形状,再进一步画出展开图.从而计算面积. 【练习】 根据下面三视图请说出物体是什么样子的 共有几层 一共需要多少个小正方体 主视图 左视图 俯视图
【感悟】这节课你有哪些收获,请在这里写一写.通过本节课的学习,我学到了...本节知识框图结构:我还有以下困惑… 【补充思考】
【检测】1.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是 (结果保留π).2.已知一个几何体的三视图如图所示,则该几何体的体积为多少?【作业】A组1.如图,圆锥的母线长为10,侧面展开图的面积为60π,则圆锥主视图的面积为 . 2.如图,礼盒的上下底面为全等的正六边形,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为 厘米. 3.如图是一个几何体的三视图(单位:cm).(1)这个几何体的名称是 ;(2)根据图中尺寸,求这个几何体的表面积.(结果保留π)4.一个等腰Rt△ABC如图所示,将它绕直线AC旋转一周,形成一个几何体.(1)写出这个几何体的名称,并画出这个几何体的三视图;(2)依据图中的测量数据,计算这个几何体的表面积.(结果保留π)B组5.如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( )A.20π B.18π C.16π D.14π6.如图2是图1长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯=( )A.a2+a B.2a2 C.a2+2a+1 D.2a2+a7.如图,是用棱长为1cm的小正方体组成的简单几何体.(1)这个几何体的体积是 cm3;(2)请画出这个几何体的三视图;(3)若在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体,画出此时的左视图.
PAGE
第4/4页
【回顾】完成下列练习:(1)如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称____.(2)一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有_____个碟子.(3)某几何体的三种视图分别如下图所示,那么这个几何体可能是( ).(A)长方体 (B)圆柱 (C)圆锥 (D)球【导入】让学生欣赏事先准备好的机械制图中三视图与对应立体图形的图片,借助图片信息让学生体会到本章知识的价值.并借此可以讲述一下现在一些中专、中技甚至大学里开设的模具和机械制图专业和课程就需要这方面的知识,激发学生的学习兴趣,导入本课. 【补充思考】
【探究】例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请你按照三视图确定制作每个密封罐所需钢板的面积. 100 100分析:对于某些立体图形,若沿其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中.三视图和展开图往往结合在一起使用.解决本题的思路是,由视图想象出密封罐的立体形状,再进一步画出展开图.从而计算面积. 【练习】 根据下面三视图请说出物体是什么样子的 共有几层 一共需要多少个小正方体 主视图 左视图 俯视图
【感悟】这节课你有哪些收获,请在这里写一写.通过本节课的学习,我学到了...本节知识框图结构:我还有以下困惑… 【补充思考】
【检测】1.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是 (结果保留π).2.已知一个几何体的三视图如图所示,则该几何体的体积为多少?【作业】A组1.如图,圆锥的母线长为10,侧面展开图的面积为60π,则圆锥主视图的面积为 . 2.如图,礼盒的上下底面为全等的正六边形,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为 厘米. 3.如图是一个几何体的三视图(单位:cm).(1)这个几何体的名称是 ;(2)根据图中尺寸,求这个几何体的表面积.(结果保留π)4.一个等腰Rt△ABC如图所示,将它绕直线AC旋转一周,形成一个几何体.(1)写出这个几何体的名称,并画出这个几何体的三视图;(2)依据图中的测量数据,计算这个几何体的表面积.(结果保留π)B组5.如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( )A.20π B.18π C.16π D.14π6.如图2是图1长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯=( )A.a2+a B.2a2 C.a2+2a+1 D.2a2+a7.如图,是用棱长为1cm的小正方体组成的简单几何体.(1)这个几何体的体积是 cm3;(2)请画出这个几何体的三视图;(3)若在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体,画出此时的左视图.
PAGE
第4/4页
