集合的基本运算
图片预览







文档简介
课件22张PPT。主讲人 : 陈楷城1.1.3集合的基本运算观察集合A,B,C元素间的关系: A={4,5,6,8},
B={3,5,7,8},
C={3,4,5,6,7,8}
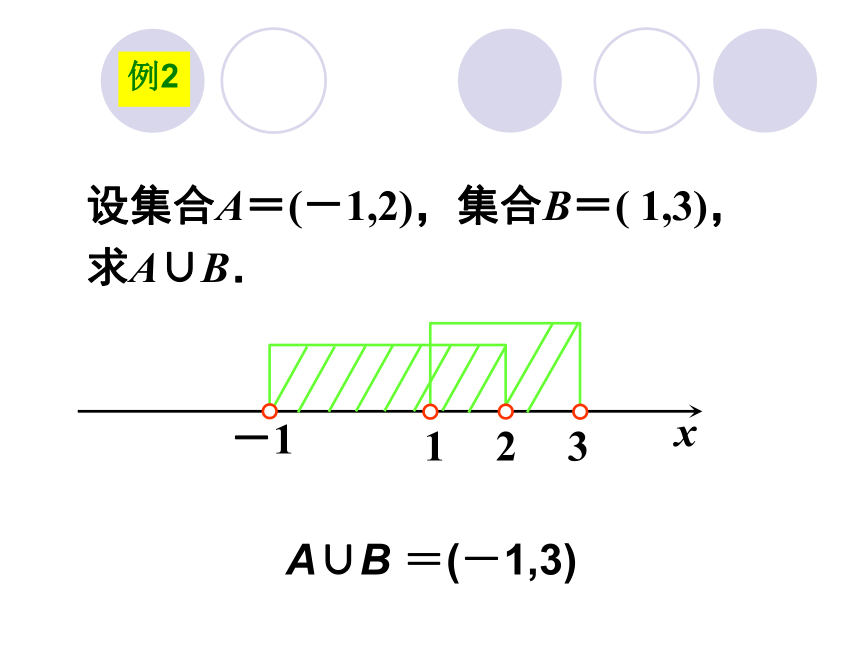
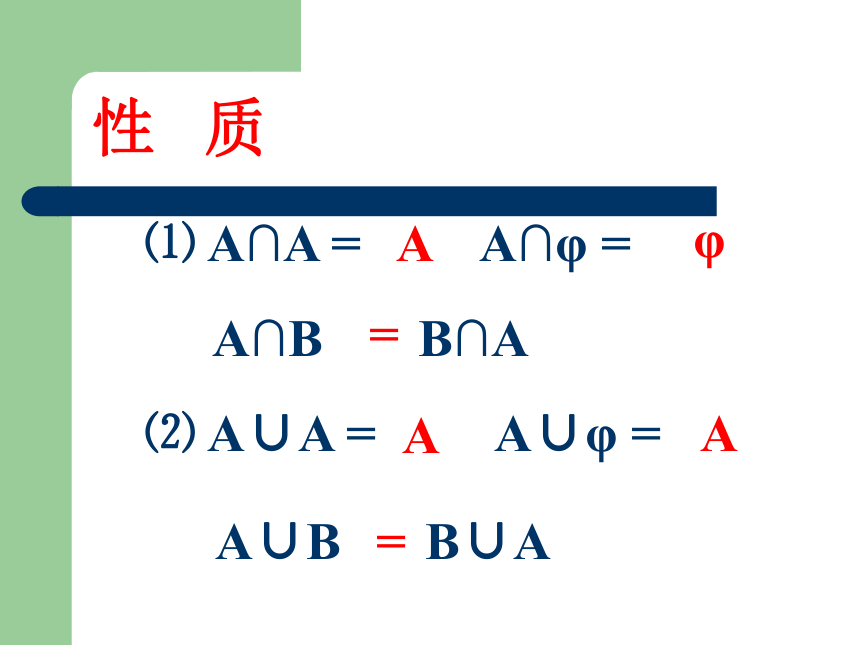
想一想并 集一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B即A∪B={x x∈A或x∈B} 读作 A并 B重点ABA∪B Wenn图设集合A={4,5,6,8},集合B={3,5,7,8,9},求A∪B.A∪B={3,4,5,6,7,8,9}.例1设集合A=(-1,2),集合B=( 1,3),求A∪B.x-1123例2A∪B =(-1,3)交 集一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.记作 A∩B 即 A∩B={x x∈A,且x∈B} 重点读作 A交 B Wenn图ABA∩B性 质⑴ A∩A = A∩φ = ⑵ A∪A = A∪φ =AAφA==B∪AA∩BB∩AA∪B新华中学开运动会。设
A={x |x是新华中学高一年级参加百米赛的同学},
B={x |x是新华中学高一年级参加跳高比赛的同学},
求A∩B, A∪B.解: A∩B={x |x是新华中学高一年级中既参加百米赛
的同学又参加跳高比赛的同学}。
A ∪ B={x |x是新华中学高一年级中参加百米赛和参加跳高比赛这两项比赛中至少一项的同学}
例3设L1,L2分别是平面内两条直线l1和l2上点的集合,试用集合的运算表示这两条直线的位置关系。解:
当两条直线l1、l2相交于一点P时,L1∩L2={P};
当两条直线l1、l2平行时,L1∩L2=Φ;
当两条直线l1、l2重合时,L1∩L2= L1=L2。例4设A={x x是等腰三角形},B={x x是直角三角形},则A∩B={x|x是等腰直角三角形}例5一般地,如果一个集合 中含有我们所要研究问题中的全部元素, 我们把它叫做全集.全 集一般地,设S是一个集合,A是S中
的一个子集, 即A?S ,则由S中所有不
属于A的元素组成的集合,叫做集合
A 相对于全集S的补集 (或余集),记做补 集重点 Wenn图设U={1,2,3,4,5,6}
A={1,3,5}
?{2,4,6}.设全集U=解:根据三角形的分类可知补集的性质若全集为U,A,则?UA7=课堂小结1. 理解两个集合交集、并集与补集的概念bb和性质.2. 用数轴法和Venn图求两个集合的运算. 教材P12 A组T6,7B组T3,再见加油!同学们!
B={3,5,7,8},
C={3,4,5,6,7,8}
想一想并 集一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B即A∪B={x x∈A或x∈B} 读作 A并 B重点ABA∪B Wenn图设集合A={4,5,6,8},集合B={3,5,7,8,9},求A∪B.A∪B={3,4,5,6,7,8,9}.例1设集合A=(-1,2),集合B=( 1,3),求A∪B.x-1123例2A∪B =(-1,3)交 集一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.记作 A∩B 即 A∩B={x x∈A,且x∈B} 重点读作 A交 B Wenn图ABA∩B性 质⑴ A∩A = A∩φ = ⑵ A∪A = A∪φ =AAφA==B∪AA∩BB∩AA∪B新华中学开运动会。设
A={x |x是新华中学高一年级参加百米赛的同学},
B={x |x是新华中学高一年级参加跳高比赛的同学},
求A∩B, A∪B.解: A∩B={x |x是新华中学高一年级中既参加百米赛
的同学又参加跳高比赛的同学}。
A ∪ B={x |x是新华中学高一年级中参加百米赛和参加跳高比赛这两项比赛中至少一项的同学}
例3设L1,L2分别是平面内两条直线l1和l2上点的集合,试用集合的运算表示这两条直线的位置关系。解:
当两条直线l1、l2相交于一点P时,L1∩L2={P};
当两条直线l1、l2平行时,L1∩L2=Φ;
当两条直线l1、l2重合时,L1∩L2= L1=L2。例4设A={x x是等腰三角形},B={x x是直角三角形},则A∩B={x|x是等腰直角三角形}例5一般地,如果一个集合 中含有我们所要研究问题中的全部元素, 我们把它叫做全集.全 集一般地,设S是一个集合,A是S中
的一个子集, 即A?S ,则由S中所有不
属于A的元素组成的集合,叫做集合
A 相对于全集S的补集 (或余集),记做补 集重点 Wenn图设U={1,2,3,4,5,6}
A={1,3,5}
?{2,4,6}.设全集U=解:根据三角形的分类可知补集的性质若全集为U,A,则?UA7=课堂小结1. 理解两个集合交集、并集与补集的概念bb和性质.2. 用数轴法和Venn图求两个集合的运算. 教材P12 A组T6,7B组T3,再见加油!同学们!
