内蒙古自治区通辽市2021-2022学年高三上学期期末考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 内蒙古自治区通辽市2021-2022学年高三上学期期末考试数学(文)试题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 959.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 00:00:00 | ||
图片预览





文档简介
通辽市2021-2022学年高三上学期期末考试
数学试卷(文科)
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. B.
C. D.
2. 复数的虚部为( )
A. B. C. D.
3. ( )
A. B. C. D.
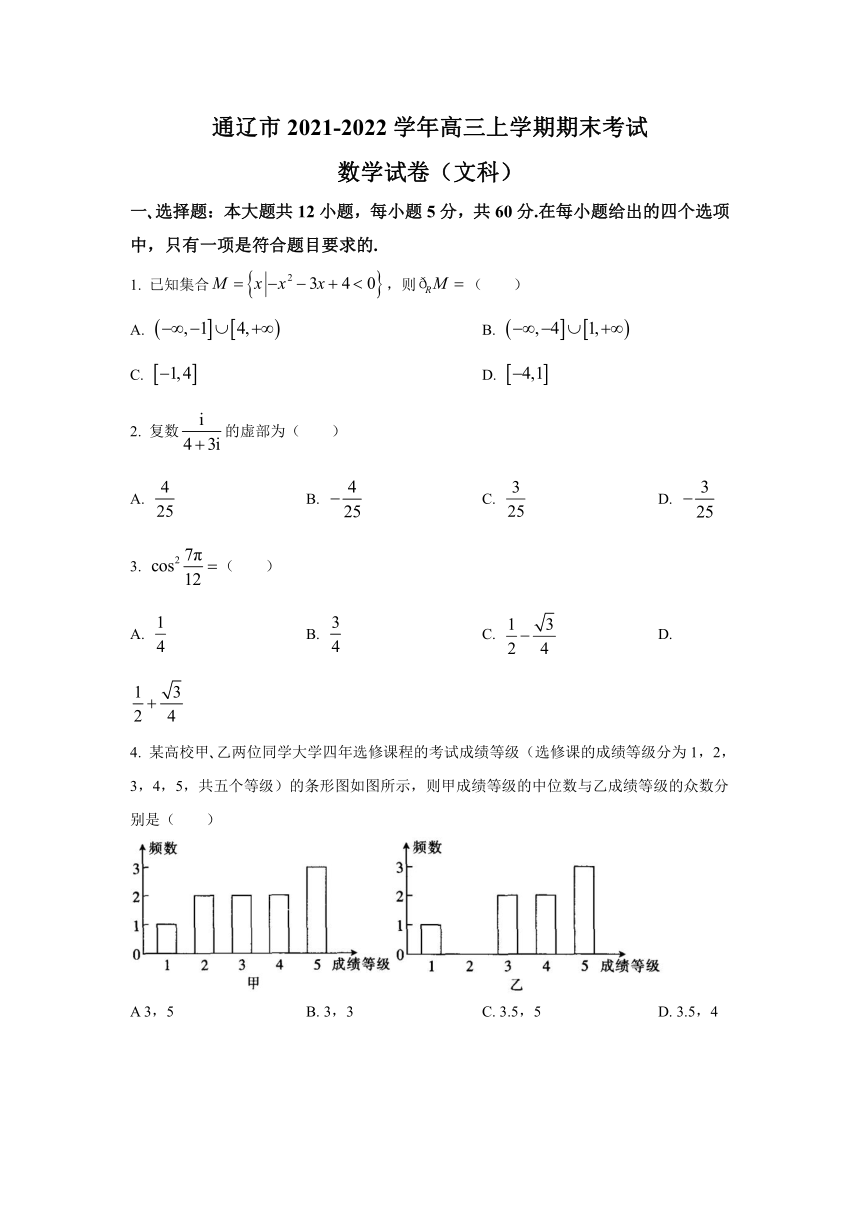
4. 某高校甲 乙两位同学大学四年选修课程的考试成绩等级(选修课的成绩等级分为1,2,3,4,5,共五个等级)的条形图如图所示,则甲成绩等级的中位数与乙成绩等级的众数分别是( )
A 3,5 B. 3,3 C. 3.5,5 D. 3.5,4
5. 若变量x,y满足约束条件则目标函数的最大值为( )
A. 5 B. 8 C. 12 D. 18
6. 将函数图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,再将所得图象向右平移个单位长度,得到函数的图象,则( )
A. B. C. D.
7. 已知一个圆锥的体积为,任取该圆锥的两条母线a,b,若a,b所成角的最大值为,则该圆锥的侧面积为( )
A. B. C. D.
8. 的内角A,B,C的对边分别为a,b,c,若,则为( )
A. 等腰非等边三角形 B. 直角三角形
C. 钝角三角形 D. 等边三角形
9. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:100血液中酒精含量在20~80之间为酒后驾车,80及以上为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1.2,且在停止喝酒以后,他血液中的酒精含量会以每小时20%的速度减少,若他想要在不违法的情况下驾驶汽车,则至少需经过的小时数约为( )(参考数据:,)
A. 6 B. 7 C. 8 D. 9
10. 已知实数a,b满足,,则( )
A. -2 B. 0 C. 1 D. 2
11. 已知F是双曲线右焦点,过F且垂直于x轴的直线交E于A,B两点,若E的渐近线上恰好存在四个点,,,,使得,则E的离心率的取值范围是( )
A. B. C. D.
12. 若函数的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称具有T性质.下列四个函数中,具有T性质的所有函数的序号为( )
①,②,③,,④
A. ①③ B. ①④ C. ①③④ D. ②③④
二 填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13. 已知平面向量,满足,则与夹角的大小为___________.
14. 如图所示,奥林匹克标志由五个互扣的环圈组成,五环象征五大洲的团结.若从该奥林匹克标志的五个环圈中任取2个,则这2个环圈恰好相交的概率为___________.
15. 根据抛物线光学性质可知,从抛物线的焦点发出的光线经该抛物线反射后与对称轴平行,一条平行于对称轴的光线经该抛物线反射后会经过抛物线的焦点.如图所示,从沿直线发出的光线经抛物线两次反射后,回到光源接收器,则该光线经过的路程为___________.
16. 已知为正方体表面上的一个动点,,是棱延长线上的一点,且,若,则动点运动轨迹的长为___________.
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
17. 为加强环境保护,治理空气污染,某环境监测部门对某市空气质量状况进行调研,随机抽査了该市100天空气中的PM2.5浓度和浓度(单位:)的数据,得到如下表格:
PM2.5
18 9 10
7 10 14
4 8 20
(1)分别估计该市一天的空气中PM2.5浓度在内和浓度在内的概率.
(2)根据以上统计数据完成下面的列联表,并判断是否有95%的把握认为该市一天的空气中PM2.5浓度与浓度有关.
PM2.5 合计
合计
附:,其中..
0.050 0.010 0005
3.841 6.635 7879
18. 已知在数列中,,,且该数列满足.
(1)求的通项公式;
(2)已知是数列的前n项和,且,求.
19. 如图,在四棱锥中,底面ABCD是平行四边形,,,,,M为BC的中点,,.
(1)证明:;
(2)求点M到平面PAD的距离.
20. 已知椭圆的焦距为4,点在G上.
(1)求椭圆G的方程;
(2)过椭圆G右焦点的直线l与椭圆G交于M,N两点,O为坐标原点,若,求直线l的方程.
21. 已知函数.
(1)当时,讨论的单调性;
(2)当时,,求a的取值范围.
22. 在极坐标系中,曲线C的极坐标方程为,以极点O为坐标原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.
(1)说明曲线C是什么曲线,并写出曲线C的一个参数方程;
(2)设P为曲线C上的一个动点,P到x,y轴的距离分别为,,求的最大值.
23. 已知函数.
(1)求不等式的解集.
(2)若不等式的解集为M,且a,证明:.
通辽市2021-2022学年高三上学期期末考试
数学试卷(文科) 答案版
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. B.
C. D.
答案 D
2. 复数的虚部为( )
A. B. C. D.
答案 A
3. ( )
A. B. C. D.
答案 C
4. 某高校甲 乙两位同学大学四年选修课程的考试成绩等级(选修课的成绩等级分为1,2,3,4,5,共五个等级)的条形图如图所示,则甲成绩等级的中位数与乙成绩等级的众数分别是( )
A 3,5 B. 3,3 C. 3.5,5 D. 3.5,4
答案 C
5. 若变量x,y满足约束条件则目标函数的最大值为( )
A. 5 B. 8 C. 12 D. 18
答案 D
6. 将函数图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,再将所得图象向右平移个单位长度,得到函数的图象,则( )
A. B. C. D.
答案 A
7. 已知一个圆锥的体积为,任取该圆锥的两条母线a,b,若a,b所成角的最大值为,则该圆锥的侧面积为( )
A. B. C. D.
答案 B
8. 的内角A,B,C的对边分别为a,b,c,若,则为( )
A. 等腰非等边三角形 B. 直角三角形
C. 钝角三角形 D. 等边三角形
答案 B
9. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:100血液中酒精含量在20~80之间为酒后驾车,80及以上为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1.2,且在停止喝酒以后,他血液中的酒精含量会以每小时20%的速度减少,若他想要在不违法的情况下驾驶汽车,则至少需经过的小时数约为( )(参考数据:,)
A. 6 B. 7 C. 8 D. 9
答案 C
10. 已知实数a,b满足,,则( )
A. -2 B. 0 C. 1 D. 2
答案 B
11. 已知F是双曲线右焦点,过F且垂直于x轴的直线交E于A,B两点,若E的渐近线上恰好存在四个点,,,,使得,则E的离心率的取值范围是( )
A. B. C. D.
答案 D
12. 若函数的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称具有T性质.下列四个函数中,具有T性质的所有函数的序号为( )
①,②,③,,④
A. ①③ B. ①④ C. ①③④ D. ②③④
答案 C
二 填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13. 已知平面向量,满足,则与夹角的大小为___________.
答案 ##
14. 如图所示,奥林匹克标志由五个互扣的环圈组成,五环象征五大洲的团结.若从该奥林匹克标志的五个环圈中任取2个,则这2个环圈恰好相交的概率为___________.
答案
15. 根据抛物线光学性质可知,从抛物线的焦点发出的光线经该抛物线反射后与对称轴平行,一条平行于对称轴的光线经该抛物线反射后会经过抛物线的焦点.如图所示,从沿直线发出的光线经抛物线两次反射后,回到光源接收器,则该光线经过的路程为___________.
答案 12
16. 已知为正方体表面上的一个动点,,是棱延长线上的一点,且,若,则动点运动轨迹的长为___________.
答案
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
17. 为加强环境保护,治理空气污染,某环境监测部门对某市空气质量状况进行调研,随机抽査了该市100天空气中的PM2.5浓度和浓度(单位:)的数据,得到如下表格:
PM2.5
18 9 10
7 10 14
4 8 20
(1)分别估计该市一天的空气中PM2.5浓度在内和浓度在内的概率.
(2)根据以上统计数据完成下面的列联表,并判断是否有95%的把握认为该市一天的空气中PM2.5浓度与浓度有关.
PM2.5 合计
合计
附:,其中..
0.050 0.010 0005
3.841 6.635 7879
答案 (1);
(2)列联表答案见解析,有95%的把握认为该市一天的空气中PM2.5浓度与浓度有关
18. 已知在数列中,,,且该数列满足.
(1)求的通项公式;
(2)已知是数列的前n项和,且,求.
答案 (1)
(2)
19. 如图,在四棱锥中,底面ABCD是平行四边形,,,,,M为BC的中点,,.
(1)证明:;
(2)求点M到平面PAD的距离.
答案 (1)证明见解析
(2)
20. 已知椭圆的焦距为4,点在G上.
(1)求椭圆G的方程;
(2)过椭圆G右焦点的直线l与椭圆G交于M,N两点,O为坐标原点,若,求直线l的方程.
答案 (1);
(2).
21. 已知函数.
(1)当时,讨论的单调性;
(2)当时,,求a的取值范围.
答案 (1)在上单调递减,在上单调递增
(2)
22. 在极坐标系中,曲线C的极坐标方程为,以极点O为坐标原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.
(1)说明曲线C是什么曲线,并写出曲线C的一个参数方程;
(2)设P为曲线C上的一个动点,P到x,y轴的距离分别为,,求的最大值.
答案 (1)曲线C是焦点在y轴上的椭圆,参数方程为(为参数)
(2)5
23. 已知函数.
(1)求不等式的解集.
(2)若不等式的解集为M,且a,证明:.
答案 (1);
(2)答案见解析.
数学试卷(文科)
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. B.
C. D.
2. 复数的虚部为( )
A. B. C. D.
3. ( )
A. B. C. D.
4. 某高校甲 乙两位同学大学四年选修课程的考试成绩等级(选修课的成绩等级分为1,2,3,4,5,共五个等级)的条形图如图所示,则甲成绩等级的中位数与乙成绩等级的众数分别是( )
A 3,5 B. 3,3 C. 3.5,5 D. 3.5,4
5. 若变量x,y满足约束条件则目标函数的最大值为( )
A. 5 B. 8 C. 12 D. 18
6. 将函数图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,再将所得图象向右平移个单位长度,得到函数的图象,则( )
A. B. C. D.
7. 已知一个圆锥的体积为,任取该圆锥的两条母线a,b,若a,b所成角的最大值为,则该圆锥的侧面积为( )
A. B. C. D.
8. 的内角A,B,C的对边分别为a,b,c,若,则为( )
A. 等腰非等边三角形 B. 直角三角形
C. 钝角三角形 D. 等边三角形
9. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:100血液中酒精含量在20~80之间为酒后驾车,80及以上为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1.2,且在停止喝酒以后,他血液中的酒精含量会以每小时20%的速度减少,若他想要在不违法的情况下驾驶汽车,则至少需经过的小时数约为( )(参考数据:,)
A. 6 B. 7 C. 8 D. 9
10. 已知实数a,b满足,,则( )
A. -2 B. 0 C. 1 D. 2
11. 已知F是双曲线右焦点,过F且垂直于x轴的直线交E于A,B两点,若E的渐近线上恰好存在四个点,,,,使得,则E的离心率的取值范围是( )
A. B. C. D.
12. 若函数的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称具有T性质.下列四个函数中,具有T性质的所有函数的序号为( )
①,②,③,,④
A. ①③ B. ①④ C. ①③④ D. ②③④
二 填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13. 已知平面向量,满足,则与夹角的大小为___________.
14. 如图所示,奥林匹克标志由五个互扣的环圈组成,五环象征五大洲的团结.若从该奥林匹克标志的五个环圈中任取2个,则这2个环圈恰好相交的概率为___________.
15. 根据抛物线光学性质可知,从抛物线的焦点发出的光线经该抛物线反射后与对称轴平行,一条平行于对称轴的光线经该抛物线反射后会经过抛物线的焦点.如图所示,从沿直线发出的光线经抛物线两次反射后,回到光源接收器,则该光线经过的路程为___________.
16. 已知为正方体表面上的一个动点,,是棱延长线上的一点,且,若,则动点运动轨迹的长为___________.
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
17. 为加强环境保护,治理空气污染,某环境监测部门对某市空气质量状况进行调研,随机抽査了该市100天空气中的PM2.5浓度和浓度(单位:)的数据,得到如下表格:
PM2.5
18 9 10
7 10 14
4 8 20
(1)分别估计该市一天的空气中PM2.5浓度在内和浓度在内的概率.
(2)根据以上统计数据完成下面的列联表,并判断是否有95%的把握认为该市一天的空气中PM2.5浓度与浓度有关.
PM2.5 合计
合计
附:,其中..
0.050 0.010 0005
3.841 6.635 7879
18. 已知在数列中,,,且该数列满足.
(1)求的通项公式;
(2)已知是数列的前n项和,且,求.
19. 如图,在四棱锥中,底面ABCD是平行四边形,,,,,M为BC的中点,,.
(1)证明:;
(2)求点M到平面PAD的距离.
20. 已知椭圆的焦距为4,点在G上.
(1)求椭圆G的方程;
(2)过椭圆G右焦点的直线l与椭圆G交于M,N两点,O为坐标原点,若,求直线l的方程.
21. 已知函数.
(1)当时,讨论的单调性;
(2)当时,,求a的取值范围.
22. 在极坐标系中,曲线C的极坐标方程为,以极点O为坐标原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.
(1)说明曲线C是什么曲线,并写出曲线C的一个参数方程;
(2)设P为曲线C上的一个动点,P到x,y轴的距离分别为,,求的最大值.
23. 已知函数.
(1)求不等式的解集.
(2)若不等式的解集为M,且a,证明:.
通辽市2021-2022学年高三上学期期末考试
数学试卷(文科) 答案版
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. B.
C. D.
答案 D
2. 复数的虚部为( )
A. B. C. D.
答案 A
3. ( )
A. B. C. D.
答案 C
4. 某高校甲 乙两位同学大学四年选修课程的考试成绩等级(选修课的成绩等级分为1,2,3,4,5,共五个等级)的条形图如图所示,则甲成绩等级的中位数与乙成绩等级的众数分别是( )
A 3,5 B. 3,3 C. 3.5,5 D. 3.5,4
答案 C
5. 若变量x,y满足约束条件则目标函数的最大值为( )
A. 5 B. 8 C. 12 D. 18
答案 D
6. 将函数图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,再将所得图象向右平移个单位长度,得到函数的图象,则( )
A. B. C. D.
答案 A
7. 已知一个圆锥的体积为,任取该圆锥的两条母线a,b,若a,b所成角的最大值为,则该圆锥的侧面积为( )
A. B. C. D.
答案 B
8. 的内角A,B,C的对边分别为a,b,c,若,则为( )
A. 等腰非等边三角形 B. 直角三角形
C. 钝角三角形 D. 等边三角形
答案 B
9. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:100血液中酒精含量在20~80之间为酒后驾车,80及以上为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1.2,且在停止喝酒以后,他血液中的酒精含量会以每小时20%的速度减少,若他想要在不违法的情况下驾驶汽车,则至少需经过的小时数约为( )(参考数据:,)
A. 6 B. 7 C. 8 D. 9
答案 C
10. 已知实数a,b满足,,则( )
A. -2 B. 0 C. 1 D. 2
答案 B
11. 已知F是双曲线右焦点,过F且垂直于x轴的直线交E于A,B两点,若E的渐近线上恰好存在四个点,,,,使得,则E的离心率的取值范围是( )
A. B. C. D.
答案 D
12. 若函数的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称具有T性质.下列四个函数中,具有T性质的所有函数的序号为( )
①,②,③,,④
A. ①③ B. ①④ C. ①③④ D. ②③④
答案 C
二 填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13. 已知平面向量,满足,则与夹角的大小为___________.
答案 ##
14. 如图所示,奥林匹克标志由五个互扣的环圈组成,五环象征五大洲的团结.若从该奥林匹克标志的五个环圈中任取2个,则这2个环圈恰好相交的概率为___________.
答案
15. 根据抛物线光学性质可知,从抛物线的焦点发出的光线经该抛物线反射后与对称轴平行,一条平行于对称轴的光线经该抛物线反射后会经过抛物线的焦点.如图所示,从沿直线发出的光线经抛物线两次反射后,回到光源接收器,则该光线经过的路程为___________.
答案 12
16. 已知为正方体表面上的一个动点,,是棱延长线上的一点,且,若,则动点运动轨迹的长为___________.
答案
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
17. 为加强环境保护,治理空气污染,某环境监测部门对某市空气质量状况进行调研,随机抽査了该市100天空气中的PM2.5浓度和浓度(单位:)的数据,得到如下表格:
PM2.5
18 9 10
7 10 14
4 8 20
(1)分别估计该市一天的空气中PM2.5浓度在内和浓度在内的概率.
(2)根据以上统计数据完成下面的列联表,并判断是否有95%的把握认为该市一天的空气中PM2.5浓度与浓度有关.
PM2.5 合计
合计
附:,其中..
0.050 0.010 0005
3.841 6.635 7879
答案 (1);
(2)列联表答案见解析,有95%的把握认为该市一天的空气中PM2.5浓度与浓度有关
18. 已知在数列中,,,且该数列满足.
(1)求的通项公式;
(2)已知是数列的前n项和,且,求.
答案 (1)
(2)
19. 如图,在四棱锥中,底面ABCD是平行四边形,,,,,M为BC的中点,,.
(1)证明:;
(2)求点M到平面PAD的距离.
答案 (1)证明见解析
(2)
20. 已知椭圆的焦距为4,点在G上.
(1)求椭圆G的方程;
(2)过椭圆G右焦点的直线l与椭圆G交于M,N两点,O为坐标原点,若,求直线l的方程.
答案 (1);
(2).
21. 已知函数.
(1)当时,讨论的单调性;
(2)当时,,求a的取值范围.
答案 (1)在上单调递减,在上单调递增
(2)
22. 在极坐标系中,曲线C的极坐标方程为,以极点O为坐标原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.
(1)说明曲线C是什么曲线,并写出曲线C的一个参数方程;
(2)设P为曲线C上的一个动点,P到x,y轴的距离分别为,,求的最大值.
答案 (1)曲线C是焦点在y轴上的椭圆,参数方程为(为参数)
(2)5
23. 已知函数.
(1)求不等式的解集.
(2)若不等式的解集为M,且a,证明:.
答案 (1);
(2)答案见解析.
同课章节目录
