2022年小升初数学总复习(通用版)第1课时 整数课件(66张PPT)
文档属性
| 名称 | 2022年小升初数学总复习(通用版)第1课时 整数课件(66张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 721.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 21:15:10 | ||
图片预览











文档简介
(共66张PPT)
2
0
2
2
2022年小升初数学复习
全国通用版
第1课时 整数
专题一 数的认识
考点知识梳理
热门考点精讲
目录
小考真题演练
考点知识梳理
1. 整数与自然数
(1)自然数:表示物体个数的1,2,3,4,5,…都是自然数。一个物体也没有,用0表示,0也是自然数。最小的自然数是0,没有最大的自然数,自然数的个数是无限的。
正整数、0和负整数统称为整数,正整数和0都是自然数。
整数的个数是无限的,没有最小的整数,也没有最大的整数。
2. 整数的计数和数位顺序表
(1)计数
计数就是数数。计数的过程就是把物体与从1开始的、由小到大的自然数建立一一对应的过程。
计数单位:一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位间的进率是“十”,这样的计数法叫做十进制计数法。
(2)数位
数位:把计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
在整数中的数位是从右往左,逐渐变大:第一位是个位,第二位是十位,第三位是百位,第四位是千位,第五位是万位,第六位是十万位,第七位是百万位,第八位是千万位,以此类推。
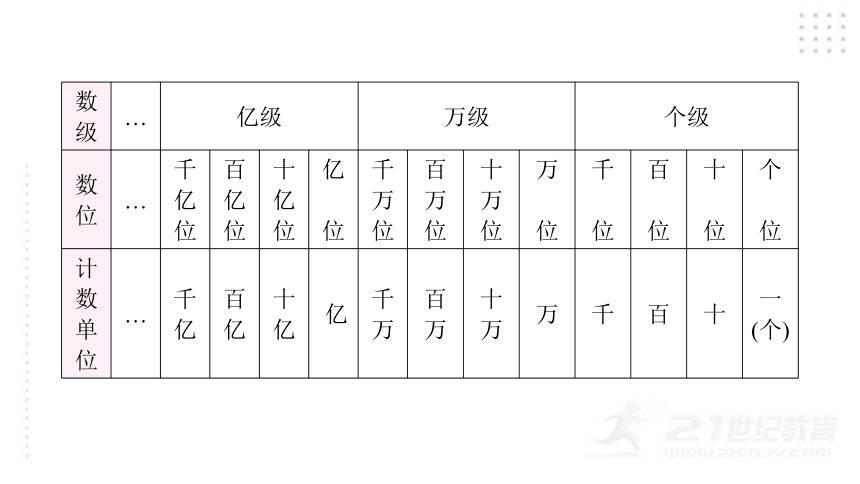
通常把按照数位的顺序从右往左排列的数位表,叫做数位顺序表,如下表。
数级 … 亿级 万级 个级 数位 … 千 亿 位 百 亿 位 十 亿 位 亿 位 千 万 位 百 万 位 十 万 位 万 位 千 位 百 位 十 位 个
位
计数 单位 … 千 亿 百 亿 十 亿 亿 千 万 百 万 十 万 万 千 百 十 一
(个)
3. 整数的读法和写法
(1)整数的读法:从高级起,一级一级往下读。 读亿级、万级时,先按照个级的数的读法去读,再在后面加一个“亿”或“万”字。每一级末尾的0都不读出来,其他数位有一个0或连续几个0都只读一个零。如8000406000 读作:八十亿零四十万六千。
(2)整数的写法: 从高级起,一级一级往下写,哪一个数位上一个单位也没有,就在那个数位上写0。如十二亿五千零四十三万写作:1250430000。
温馨提示:写数时,要注意0的占位问题。如二百四十万零六,写数时万位、千位、百位、十位都要写0占位,应写成2400006,而不能写成24006。
4. 整数的改写
(1)整万、整亿数的改写方法
把万位后面的4个0或亿位后面的8个0省略,再加上一个“万”或“亿”字。
(2)非整万、整亿数的改写方法
在万位或亿位数字的右下角点上小数点,去掉小数末尾的0,再在小数后面加上“万”或“亿”字。
(3) 把一个数省略尾数改写成用“万”或“亿”作单位
先用“四舍五入”法省略万位或亿位后面的尾数求出近似数,再在后面加一个“万”字或“亿”字,并用“≈”连接。
5. 因数和倍数
(1)如果a÷b=c(a,b,c均为非零自然数),那么a是b和c的倍数,b和c是a的因数。倍数和因数是相互依存的。
注意:为了方便,在研究因数和倍数的时候,我们所说的数均指的是非0的自然数。
(2)一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
6. 奇数和偶数
(1) 奇数:在自然数中,不是2的倍数的数叫做奇数。
(2) 偶数:在自然数中,是2的倍数的数叫做偶数。(0也是偶数)
(3)自然数中,不是奇数就是偶数。最小的奇数是1,没有最大的奇数;最小的偶数是0,没有最大的偶数。
(4)奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数,
奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数。
7. 质数和合数、分解质因数
(1)质数和合数
①质数:一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。最小的质数是2,2是唯一的偶质数,没有最大的质数。
②合数:一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。最小的合数是4,没有最大的合数。
③1既不是质数,也不是合数。
(2)分解质因数
①质因数:每个合数都可以写成几个质数相乘的形式,这几个质数就都叫做这个合数的质因数。如果一个质数是某个数的因数,那么就说这个质数是这个数的质因数。
②分解质因数:把一个合数用几个质数相乘的形式表示出来,叫做分解质因数。
③分解质因数的方法:把一个合数分解质因数,通常运用短除法。分解质因数时,先用这个合数的质因数(通常从最小的开始)去除,如果得出的商是质数,就把除数和商写成相乘的形式;如果得出的商是合数,就照上面的方法继续除下去,直到得出的商是质数为止,然后把除数和最后的商写成连乘的形式。
温馨提示:只有合数才能分解质因数,一个数的质因数的个数是有限的。
8. 2、3、5的倍数的特征
2的倍数的特征: 个位上是0,2,4,6,8的数都是2的倍数。
3的倍数的特征: 各个数位上数字的和是3的倍数,这个数就是3的倍数。
5的倍数的特征: 个位上是0或5的数都是5的倍数。
既是2的倍数又是5的倍数的特征:个位上是0。
9. 最大公因数和最小公倍数
(1)最大公因数和最小公倍数的含义:几个数公有的因数,叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数;几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
(2)求最大公因数和最小公倍数的常用方法
①先判断是否为倍数关系。(如果两个数存在倍数关系,那么较小的数是这两个数的最大公因数,较大的数是这两个数的最小公倍数。例如:15和45)
②再判断是否只有公因数1。(如果两个数是互质数,那么它们的最大公因数是1,最小公倍数是这两个数的乘积。例如:5和7,8和9是互质数)
③最后应用短除法。(先用这两个数公有的质因数连续去除,一直除到所得的商是互质数为止。若把所有的除数连乘起来,求得的就是它们的最大公因数;若把所有的除数和最后的商连乘起来,求得的就是它们的最小公倍数)
热门考点精讲
考点1:整数的读法与写法
读出或写出横线上的数。
(1)某养鸡场有9080只鸡。
读作:______________________________
(2)南京长江大桥公路桥长4589米。
读作:______________________________
(3)世界第一大洋——太平洋的平均深度为四千零二十八米,在四大洋中是最深的。
写作:______________________________
(4)长江是中国第一大河。它的全长约六千三百千米,为世界第三长河。
写作:______________________________
方法指导: 此题考查整数的读法与写法。注意读数和写数都要从高位起,千位上是几就读几千,百位上是几就读几百,十位上是几就读几十,个位上是几就读几;几千就在千位写几,几百就在百位写几,几十就在十位写几,几就在个位写几,以此类推。
答案:(1)九千零八十 (2)四千五百八十九
(3)4028 (4)6300
1. 用三个2和两个0组成一个五位数,只读一个“零”的数是
( )
A. 22200 B. 20202 C. 22002
C
2. 读出或写出下面各数。
(1)80300 读作:( )。
(2)50703007 读作:( )。
(3)四千二百万零三百 写作:( )。
(4)六亿零三百四十万 写作:( )。
八万零三百
五千零七十万三千零七
42000300
603400000
3. 用0,2,1,6组成的四位数中,最大的数是( ),最小的数是( )。
易错点拨:读数时,对“0”是否要读和读几个常错。
6210
1026
考点2:整数的改写与省略
一个九位数,最高位上的数字是最小的质数,千万位上是最小的奇数,万位上是最小的合数,百位上是最大的一位数,其余各位上均是最小的自然数,这个数是( ),读作
( ),改写成用“万”作单位的数是( )万,省略亿位后面的尾数约是( )亿。
方法指导:此题考查对质数、合数、奇数、偶数、自然数、数的组成等的掌握情况。首先要求写数、读数,然后根据写出来的数进行改写,求近似数。我们知道最小的质数是2,最小的奇数是1,最小的合数是4,最大的一位数是9,最小的自然数是0,而这个数的最高位是亿位,所以它的亿位上是2,千万位上是1,万位上是4,百位上是9,其余各位都是0。
答案:210040900 二亿一千零四万零九百
21004.09 2
4. 用四个3和五个0组成一个九位数,一个0都不读的最大九位数是( ),把它改写成用“万”作单位的数是( )万,省略亿位后面的尾数约是( )亿。
333300000
33330
3
5. 一个数的亿位和十万位上的数字都是最小的合数,千万位上的数是亿位上的数的2倍,千位上的数字是最小的质数,其余各位上的数字都是0,这个数是( ),读作( ),改写成用“万”作单位的数是( )万,省略亿位后面的尾数约是( )亿。
易错点拨:对“改写”和“省略”的理解不到位。
480402000
四亿八千零四十万二千
48040.2
5
考点3:奇数、偶数、质数、合数的特点
在自然数1~20中,既是奇数又是合数的是( ),既是偶数又是质数的是( ),( )既不是质数也不是合数。
方法指导:要答对这道题,需掌握奇数、偶数、质数、合数的概念,然后细心判断。 在自然数1~20中,奇数有1,3,5,7,9,11,13,15,17,19;合数有4,6,8,9,10,12,14,15,16,18,20;偶数有2,4,6,8,10,12,14,16,18,20;质数有2,3,5,7,11,13,17,19。所以既是奇数又是合数的是9,15,既是偶数又是质数的是2。 另外,我们知道1既不是质数也不是合数。
答案:9,1521
6. 在非0自然数中, 最小的偶数是( ),最小的奇数是( ),最小的合数是( ),最小的质数是( )。
7. 在1,2,3,9,24,41,51中,奇数是( ),偶数是( ),质数是( ),合数是( ),
( )是奇数但不是质数,( )是偶数但不是合数。
2
1
4
2
1,3,9,41,51
2,24
2,3,41
9,24,51
1,9,51
2
8. 用0,4,5组成的三位数中,最大的偶数是( ),最小的奇数是( )。
易错点拨:对奇数、偶数、质数和合数的概念掌握不到位。
540
405
考点4:2、3、5的倍数的特征
四位数7□3□既是2的倍数,又是5的倍数,同时还是3的倍数,这个四位数是( )。
方法指导: 此题考查的是2,3,5的倍数的特征。 一个数同时是2,3,5的倍数,这个数个位上的数字一定是0,并且各个数位上的数字之和是3的倍数。 因为7+3+0=10,所以这个四位数百位上的数字是2,5或8。
答案: 7230,7530或7830
9. 既是2的倍数,又是5的倍数,同时还是3的倍数的最大三位数是( )。
10.100以内同时是2,3,5的倍数的数有( )。
990
30,60,90
11. 从下面4张数字卡片中选出3张,按要求组成三位数。(每小题写出2个数即可)
(1)2的倍数:( )
(2)3的倍数: ( )
(3)5的倍数: ( )
(4)2和3的公倍数: ( )
(5)2和5的公倍数: ( )
104,140
105,450
140,145
150,540
140,510
(答案不唯一)
考点5:最大公因数的应用
李奶奶买芒果花了16元,王奶奶买芒果花了24元。如果她们买的芒果的单价是一样的,那么这种芒果的单价最高是多少元?(她们购买芒果的单价和数量都是整数)
方法指导:此题考查的是最大公因数的应用。因为她们买的芒果的单价是一样的,所以芒果的单价既是16的因数,又是24的因数,所以本题实质上是求16和24这两个数的最大公因数,也就是这两个数的公有质因数的连乘积。
答案:本题实质上是求16和24这两个数的最大公因数。16=2×2×2×2
24=2×2×2×3
故16和24的最大公因数是2×2×2=8。
答:这种芒果的单价最高是8元。
12. 已知甲=2×3×5×7,乙=2×2×5×7,那么甲和乙的最大公因数是( )
A. 7 B. 2×5×7
C. 2×3×5×7 D. 5×7
B
13. 有3根木料,分别长120 cm,180 cm,300 cm。现在要把它们截成同样长的小段,且每根木料都不能有剩余,每小段最长是
( )cm,一共可以截成( )段。
60
10
14. 一块木板长120 cm,宽90 cm,要锯成若干个正方形,而且没有剩余,如果使正方形的边长最长,它可以锯成多少个正方形?
120=2×2×2×3×5,90=2×3×3×5
所以120和90的最大公因数是2×3×5=30,即正方形木板的边长是30 cm。
(120÷30)×(90÷30)=4×3=12(个)
答:正方形木板的边长最长是30 cm,它可以锯成12个正方形。
考点6:最小公倍数的应用
暑假期间,婷婷和丹丹去敬老院照顾老人。7月7日她们都去了敬老院,并约定婷婷每隔2天去一次,丹丹每隔3天去一次。
(1)8月份,她们第一次同时去敬老院的日子是几号
(2)从7月7日到8月31日,她们一起去敬老院的情况共有多少次
方法指导: 此题是用最小公倍数的知识解决实际生活中的问题,培养学生的分析、 应用能力。婷婷每隔2天去一次,即每3天去一次,那么经过的天数应是3的倍数。同理,丹丹去敬老院所经过的天数应是4的倍数。由此得知两人再一次同去敬老院的日子距离7月7日的天数就是3和4的最小公倍数。
(1)3×4=12,从7月7日起每过12天同去一次,过24天正好是7月31日,所以8月份她们第一次同时去敬老院的日子是8月12日。
(2)由(1)可得,两人每12天同去一次,7月7日后第55天是8月31日,55÷12=4……7,两人同去的次数是4+1=5(次)(应加上7月7日的这次)。
答案:(1)8月份,她们第一次同时去敬老院的日子是8月12日。
(2)从7月7日到8月31日,她们一起去敬老院的情况共有5次。
15. 如果甲=2×5,乙=2×3,那么甲、乙两数的最小公倍数是( )
A. 2 B. 15
C. 30 D. 60
C
16. 一堆多于15个少于20个的桃子,2个2个地分剩下1个,3个3个地分也剩下1个,这堆桃子有( )个。
19
17. 英雄广场站有三条公交车线路,第一条线路每8分钟发一班车,第二条线路每10分钟发一班车,第三条线路每16分钟发一班车。已知早上6:00这三条线路的公交车同时发车,且该站发出最后一班车的时间是20:00,求该站最后一次三条线路的公交车同时发车是什么时刻。
8,10,16的最小公倍数是80,
(20-6)×60=840(分钟)
840÷80=10……40(分钟)
答:最后一次三条线路的公交车同时发车是19:20。
小考真题演练
一 填空题。
1. 如果向北走50 m记作+50 m,那么向南走100 m可记作
( )。
2. 60600600是一个( )位数,从右往左数,第二个6在
( )位上,第一个6表示6个( ),这个数读作
( )。
-100 m
八
十万
百
六千零六十万零六百
3. 8650654000读作( ),改写成用“万”作单位的数是( )万; 省略亿位后面的尾数约是( )亿。
4. 一个九位数,任意两个相邻数位上的数字的和是9,其中万位上是最小的合数,这个数是( )。
八十六亿五千零六十五万四千
865065.4
87
454545454
5. 18和45的公因数有( ),最大公因数是(9),最小公倍数是( )。
6. 一个三位数,它同时是2,3,5的倍数,这个数最小是
( )。
7. 甲、乙两数的最大公因数是3,最小公倍数是45,如果甲数是9,那么乙数是( );如果甲数是45,那么乙数是( )。
1,3,9
90
120
15
3
8. 5050500读作( ),
八百零三亿零七十万写作( )。
9. 一个数“四舍五入”到万位是15万,这个数最大是
( ),最小是( )。
10. 一个三位数:46□,当它是2的倍数时,□里最大填
( );当它是3的倍数时,□里最小填( )。
五百零五万零五百
80300700000
154999
145000
8
8
2
二 选择题。(将正确答案的字母编号填在括号里)
1. 读60000904000时,( )。
A. 一个零也不读 B. 只读一个零
C. 读两个零 D. 读三个零
B
2. 一个合数( )因数。
A. 没有 B. 只有一个
C. 只有两个 D. 有三个或三个以上
3. 下列数中,与200万最接近的数是( )。
A.2001000 B.2010000
C. 1999999 D. 199万
D
C
4. 由8个十万、5个千和6个一组成的数是( )。
A.80506 B.850560
C.805006 D.85006
5. 一个数的最高位是百亿位,那么这个数是( )位数。
A. 十二 B. 十一 C. 十 D. 九
C
B
6. 用一个1和三个9组成的最大的四位数是( )。
A. 1999 B.9919
C.9991 D.9199
7. 79996≈80万,里可以填( )个数。
A. 1 B. 4 C. 5 D.6
C
C
8. 用4,5,7,8这四个数,能组成( )对互质数。
A.2 B. 3 C. 4 D.5
9. 4是12和36的( )。
A. 最小公倍数 B. 倍数
C. 最大公因数 D. 公因数
D
D
10. 乙数是甲数的倍数,甲数是丙数的倍数,它们三个的最小公倍数是( )。
A.丙数 B. 乙数
C. 甲数 D.都不是
B
三 按要求完成下列各题。
1. 用8,3,7,0,0,0,0组成一个七位数。(每种情况只写一个数)
(1)只读一个零的数:______________________________。
(2)读两个零的数:______________________________。
(3)一个零都不读的数:______________________________。
(4)与7000000最接近的数:____________________________。
(5)万位上的数字是0的最大七位数:______________________。
8000037
8000307
8003700
7000038
8703000
(前3小题答案不唯一)
2. 读出下面横线上的数。
(1)俄罗斯的国土面积大约是17098200平方千米。
读作:______________________________
(2)日本的国土面积大约是378000平方千米。
读作:______________________________
(3)美国的国土面积大约是9629091平方千米。
读作:______________________________
一千七百零九万八千二百
三十七万八千
九百六十二万九千零九十一
四 解决问题。
1. 一个四位数,它的十位上的数字是6,百位上的数比十位上的数少3,千位上的数比十位上的数多1,个位上是最大的一位数,这个数是多少?
百位上的数是6-3=3,千位上的数是6+1=7,
最大的一位数是9。
答:这个数是7369。
2. 同学们排队做操,不论是每行8人,还是每行10人,或是每行12人,最后都正好多出5人。至少有多少人做操
8,10,12的最小公倍数是120,
120+5=125(人)
答:至少有125人做操。
3. 要把它们截成同样长的小棒,不能有剩余,每根小棒最长是多少厘米?
32=2×2×2×2×248=2×2×2×2×3
所以32和48的最大公因数是2×2×2×2=16,
即每根小棒最长是16 cm。
答:每根小棒最长是16 cm。
2
0
2
2
2022年小升初数学复习
全国通用版
第1课时 整数
专题一 数的认识
考点知识梳理
热门考点精讲
目录
小考真题演练
考点知识梳理
1. 整数与自然数
(1)自然数:表示物体个数的1,2,3,4,5,…都是自然数。一个物体也没有,用0表示,0也是自然数。最小的自然数是0,没有最大的自然数,自然数的个数是无限的。
正整数、0和负整数统称为整数,正整数和0都是自然数。
整数的个数是无限的,没有最小的整数,也没有最大的整数。
2. 整数的计数和数位顺序表
(1)计数
计数就是数数。计数的过程就是把物体与从1开始的、由小到大的自然数建立一一对应的过程。
计数单位:一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位间的进率是“十”,这样的计数法叫做十进制计数法。
(2)数位
数位:把计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
在整数中的数位是从右往左,逐渐变大:第一位是个位,第二位是十位,第三位是百位,第四位是千位,第五位是万位,第六位是十万位,第七位是百万位,第八位是千万位,以此类推。
通常把按照数位的顺序从右往左排列的数位表,叫做数位顺序表,如下表。
数级 … 亿级 万级 个级 数位 … 千 亿 位 百 亿 位 十 亿 位 亿 位 千 万 位 百 万 位 十 万 位 万 位 千 位 百 位 十 位 个
位
计数 单位 … 千 亿 百 亿 十 亿 亿 千 万 百 万 十 万 万 千 百 十 一
(个)
3. 整数的读法和写法
(1)整数的读法:从高级起,一级一级往下读。 读亿级、万级时,先按照个级的数的读法去读,再在后面加一个“亿”或“万”字。每一级末尾的0都不读出来,其他数位有一个0或连续几个0都只读一个零。如8000406000 读作:八十亿零四十万六千。
(2)整数的写法: 从高级起,一级一级往下写,哪一个数位上一个单位也没有,就在那个数位上写0。如十二亿五千零四十三万写作:1250430000。
温馨提示:写数时,要注意0的占位问题。如二百四十万零六,写数时万位、千位、百位、十位都要写0占位,应写成2400006,而不能写成24006。
4. 整数的改写
(1)整万、整亿数的改写方法
把万位后面的4个0或亿位后面的8个0省略,再加上一个“万”或“亿”字。
(2)非整万、整亿数的改写方法
在万位或亿位数字的右下角点上小数点,去掉小数末尾的0,再在小数后面加上“万”或“亿”字。
(3) 把一个数省略尾数改写成用“万”或“亿”作单位
先用“四舍五入”法省略万位或亿位后面的尾数求出近似数,再在后面加一个“万”字或“亿”字,并用“≈”连接。
5. 因数和倍数
(1)如果a÷b=c(a,b,c均为非零自然数),那么a是b和c的倍数,b和c是a的因数。倍数和因数是相互依存的。
注意:为了方便,在研究因数和倍数的时候,我们所说的数均指的是非0的自然数。
(2)一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
6. 奇数和偶数
(1) 奇数:在自然数中,不是2的倍数的数叫做奇数。
(2) 偶数:在自然数中,是2的倍数的数叫做偶数。(0也是偶数)
(3)自然数中,不是奇数就是偶数。最小的奇数是1,没有最大的奇数;最小的偶数是0,没有最大的偶数。
(4)奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数,
奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数。
7. 质数和合数、分解质因数
(1)质数和合数
①质数:一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。最小的质数是2,2是唯一的偶质数,没有最大的质数。
②合数:一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。最小的合数是4,没有最大的合数。
③1既不是质数,也不是合数。
(2)分解质因数
①质因数:每个合数都可以写成几个质数相乘的形式,这几个质数就都叫做这个合数的质因数。如果一个质数是某个数的因数,那么就说这个质数是这个数的质因数。
②分解质因数:把一个合数用几个质数相乘的形式表示出来,叫做分解质因数。
③分解质因数的方法:把一个合数分解质因数,通常运用短除法。分解质因数时,先用这个合数的质因数(通常从最小的开始)去除,如果得出的商是质数,就把除数和商写成相乘的形式;如果得出的商是合数,就照上面的方法继续除下去,直到得出的商是质数为止,然后把除数和最后的商写成连乘的形式。
温馨提示:只有合数才能分解质因数,一个数的质因数的个数是有限的。
8. 2、3、5的倍数的特征
2的倍数的特征: 个位上是0,2,4,6,8的数都是2的倍数。
3的倍数的特征: 各个数位上数字的和是3的倍数,这个数就是3的倍数。
5的倍数的特征: 个位上是0或5的数都是5的倍数。
既是2的倍数又是5的倍数的特征:个位上是0。
9. 最大公因数和最小公倍数
(1)最大公因数和最小公倍数的含义:几个数公有的因数,叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数;几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
(2)求最大公因数和最小公倍数的常用方法
①先判断是否为倍数关系。(如果两个数存在倍数关系,那么较小的数是这两个数的最大公因数,较大的数是这两个数的最小公倍数。例如:15和45)
②再判断是否只有公因数1。(如果两个数是互质数,那么它们的最大公因数是1,最小公倍数是这两个数的乘积。例如:5和7,8和9是互质数)
③最后应用短除法。(先用这两个数公有的质因数连续去除,一直除到所得的商是互质数为止。若把所有的除数连乘起来,求得的就是它们的最大公因数;若把所有的除数和最后的商连乘起来,求得的就是它们的最小公倍数)
热门考点精讲
考点1:整数的读法与写法
读出或写出横线上的数。
(1)某养鸡场有9080只鸡。
读作:______________________________
(2)南京长江大桥公路桥长4589米。
读作:______________________________
(3)世界第一大洋——太平洋的平均深度为四千零二十八米,在四大洋中是最深的。
写作:______________________________
(4)长江是中国第一大河。它的全长约六千三百千米,为世界第三长河。
写作:______________________________
方法指导: 此题考查整数的读法与写法。注意读数和写数都要从高位起,千位上是几就读几千,百位上是几就读几百,十位上是几就读几十,个位上是几就读几;几千就在千位写几,几百就在百位写几,几十就在十位写几,几就在个位写几,以此类推。
答案:(1)九千零八十 (2)四千五百八十九
(3)4028 (4)6300
1. 用三个2和两个0组成一个五位数,只读一个“零”的数是
( )
A. 22200 B. 20202 C. 22002
C
2. 读出或写出下面各数。
(1)80300 读作:( )。
(2)50703007 读作:( )。
(3)四千二百万零三百 写作:( )。
(4)六亿零三百四十万 写作:( )。
八万零三百
五千零七十万三千零七
42000300
603400000
3. 用0,2,1,6组成的四位数中,最大的数是( ),最小的数是( )。
易错点拨:读数时,对“0”是否要读和读几个常错。
6210
1026
考点2:整数的改写与省略
一个九位数,最高位上的数字是最小的质数,千万位上是最小的奇数,万位上是最小的合数,百位上是最大的一位数,其余各位上均是最小的自然数,这个数是( ),读作
( ),改写成用“万”作单位的数是( )万,省略亿位后面的尾数约是( )亿。
方法指导:此题考查对质数、合数、奇数、偶数、自然数、数的组成等的掌握情况。首先要求写数、读数,然后根据写出来的数进行改写,求近似数。我们知道最小的质数是2,最小的奇数是1,最小的合数是4,最大的一位数是9,最小的自然数是0,而这个数的最高位是亿位,所以它的亿位上是2,千万位上是1,万位上是4,百位上是9,其余各位都是0。
答案:210040900 二亿一千零四万零九百
21004.09 2
4. 用四个3和五个0组成一个九位数,一个0都不读的最大九位数是( ),把它改写成用“万”作单位的数是( )万,省略亿位后面的尾数约是( )亿。
333300000
33330
3
5. 一个数的亿位和十万位上的数字都是最小的合数,千万位上的数是亿位上的数的2倍,千位上的数字是最小的质数,其余各位上的数字都是0,这个数是( ),读作( ),改写成用“万”作单位的数是( )万,省略亿位后面的尾数约是( )亿。
易错点拨:对“改写”和“省略”的理解不到位。
480402000
四亿八千零四十万二千
48040.2
5
考点3:奇数、偶数、质数、合数的特点
在自然数1~20中,既是奇数又是合数的是( ),既是偶数又是质数的是( ),( )既不是质数也不是合数。
方法指导:要答对这道题,需掌握奇数、偶数、质数、合数的概念,然后细心判断。 在自然数1~20中,奇数有1,3,5,7,9,11,13,15,17,19;合数有4,6,8,9,10,12,14,15,16,18,20;偶数有2,4,6,8,10,12,14,16,18,20;质数有2,3,5,7,11,13,17,19。所以既是奇数又是合数的是9,15,既是偶数又是质数的是2。 另外,我们知道1既不是质数也不是合数。
答案:9,1521
6. 在非0自然数中, 最小的偶数是( ),最小的奇数是( ),最小的合数是( ),最小的质数是( )。
7. 在1,2,3,9,24,41,51中,奇数是( ),偶数是( ),质数是( ),合数是( ),
( )是奇数但不是质数,( )是偶数但不是合数。
2
1
4
2
1,3,9,41,51
2,24
2,3,41
9,24,51
1,9,51
2
8. 用0,4,5组成的三位数中,最大的偶数是( ),最小的奇数是( )。
易错点拨:对奇数、偶数、质数和合数的概念掌握不到位。
540
405
考点4:2、3、5的倍数的特征
四位数7□3□既是2的倍数,又是5的倍数,同时还是3的倍数,这个四位数是( )。
方法指导: 此题考查的是2,3,5的倍数的特征。 一个数同时是2,3,5的倍数,这个数个位上的数字一定是0,并且各个数位上的数字之和是3的倍数。 因为7+3+0=10,所以这个四位数百位上的数字是2,5或8。
答案: 7230,7530或7830
9. 既是2的倍数,又是5的倍数,同时还是3的倍数的最大三位数是( )。
10.100以内同时是2,3,5的倍数的数有( )。
990
30,60,90
11. 从下面4张数字卡片中选出3张,按要求组成三位数。(每小题写出2个数即可)
(1)2的倍数:( )
(2)3的倍数: ( )
(3)5的倍数: ( )
(4)2和3的公倍数: ( )
(5)2和5的公倍数: ( )
104,140
105,450
140,145
150,540
140,510
(答案不唯一)
考点5:最大公因数的应用
李奶奶买芒果花了16元,王奶奶买芒果花了24元。如果她们买的芒果的单价是一样的,那么这种芒果的单价最高是多少元?(她们购买芒果的单价和数量都是整数)
方法指导:此题考查的是最大公因数的应用。因为她们买的芒果的单价是一样的,所以芒果的单价既是16的因数,又是24的因数,所以本题实质上是求16和24这两个数的最大公因数,也就是这两个数的公有质因数的连乘积。
答案:本题实质上是求16和24这两个数的最大公因数。16=2×2×2×2
24=2×2×2×3
故16和24的最大公因数是2×2×2=8。
答:这种芒果的单价最高是8元。
12. 已知甲=2×3×5×7,乙=2×2×5×7,那么甲和乙的最大公因数是( )
A. 7 B. 2×5×7
C. 2×3×5×7 D. 5×7
B
13. 有3根木料,分别长120 cm,180 cm,300 cm。现在要把它们截成同样长的小段,且每根木料都不能有剩余,每小段最长是
( )cm,一共可以截成( )段。
60
10
14. 一块木板长120 cm,宽90 cm,要锯成若干个正方形,而且没有剩余,如果使正方形的边长最长,它可以锯成多少个正方形?
120=2×2×2×3×5,90=2×3×3×5
所以120和90的最大公因数是2×3×5=30,即正方形木板的边长是30 cm。
(120÷30)×(90÷30)=4×3=12(个)
答:正方形木板的边长最长是30 cm,它可以锯成12个正方形。
考点6:最小公倍数的应用
暑假期间,婷婷和丹丹去敬老院照顾老人。7月7日她们都去了敬老院,并约定婷婷每隔2天去一次,丹丹每隔3天去一次。
(1)8月份,她们第一次同时去敬老院的日子是几号
(2)从7月7日到8月31日,她们一起去敬老院的情况共有多少次
方法指导: 此题是用最小公倍数的知识解决实际生活中的问题,培养学生的分析、 应用能力。婷婷每隔2天去一次,即每3天去一次,那么经过的天数应是3的倍数。同理,丹丹去敬老院所经过的天数应是4的倍数。由此得知两人再一次同去敬老院的日子距离7月7日的天数就是3和4的最小公倍数。
(1)3×4=12,从7月7日起每过12天同去一次,过24天正好是7月31日,所以8月份她们第一次同时去敬老院的日子是8月12日。
(2)由(1)可得,两人每12天同去一次,7月7日后第55天是8月31日,55÷12=4……7,两人同去的次数是4+1=5(次)(应加上7月7日的这次)。
答案:(1)8月份,她们第一次同时去敬老院的日子是8月12日。
(2)从7月7日到8月31日,她们一起去敬老院的情况共有5次。
15. 如果甲=2×5,乙=2×3,那么甲、乙两数的最小公倍数是( )
A. 2 B. 15
C. 30 D. 60
C
16. 一堆多于15个少于20个的桃子,2个2个地分剩下1个,3个3个地分也剩下1个,这堆桃子有( )个。
19
17. 英雄广场站有三条公交车线路,第一条线路每8分钟发一班车,第二条线路每10分钟发一班车,第三条线路每16分钟发一班车。已知早上6:00这三条线路的公交车同时发车,且该站发出最后一班车的时间是20:00,求该站最后一次三条线路的公交车同时发车是什么时刻。
8,10,16的最小公倍数是80,
(20-6)×60=840(分钟)
840÷80=10……40(分钟)
答:最后一次三条线路的公交车同时发车是19:20。
小考真题演练
一 填空题。
1. 如果向北走50 m记作+50 m,那么向南走100 m可记作
( )。
2. 60600600是一个( )位数,从右往左数,第二个6在
( )位上,第一个6表示6个( ),这个数读作
( )。
-100 m
八
十万
百
六千零六十万零六百
3. 8650654000读作( ),改写成用“万”作单位的数是( )万; 省略亿位后面的尾数约是( )亿。
4. 一个九位数,任意两个相邻数位上的数字的和是9,其中万位上是最小的合数,这个数是( )。
八十六亿五千零六十五万四千
865065.4
87
454545454
5. 18和45的公因数有( ),最大公因数是(9),最小公倍数是( )。
6. 一个三位数,它同时是2,3,5的倍数,这个数最小是
( )。
7. 甲、乙两数的最大公因数是3,最小公倍数是45,如果甲数是9,那么乙数是( );如果甲数是45,那么乙数是( )。
1,3,9
90
120
15
3
8. 5050500读作( ),
八百零三亿零七十万写作( )。
9. 一个数“四舍五入”到万位是15万,这个数最大是
( ),最小是( )。
10. 一个三位数:46□,当它是2的倍数时,□里最大填
( );当它是3的倍数时,□里最小填( )。
五百零五万零五百
80300700000
154999
145000
8
8
2
二 选择题。(将正确答案的字母编号填在括号里)
1. 读60000904000时,( )。
A. 一个零也不读 B. 只读一个零
C. 读两个零 D. 读三个零
B
2. 一个合数( )因数。
A. 没有 B. 只有一个
C. 只有两个 D. 有三个或三个以上
3. 下列数中,与200万最接近的数是( )。
A.2001000 B.2010000
C. 1999999 D. 199万
D
C
4. 由8个十万、5个千和6个一组成的数是( )。
A.80506 B.850560
C.805006 D.85006
5. 一个数的最高位是百亿位,那么这个数是( )位数。
A. 十二 B. 十一 C. 十 D. 九
C
B
6. 用一个1和三个9组成的最大的四位数是( )。
A. 1999 B.9919
C.9991 D.9199
7. 79996≈80万,里可以填( )个数。
A. 1 B. 4 C. 5 D.6
C
C
8. 用4,5,7,8这四个数,能组成( )对互质数。
A.2 B. 3 C. 4 D.5
9. 4是12和36的( )。
A. 最小公倍数 B. 倍数
C. 最大公因数 D. 公因数
D
D
10. 乙数是甲数的倍数,甲数是丙数的倍数,它们三个的最小公倍数是( )。
A.丙数 B. 乙数
C. 甲数 D.都不是
B
三 按要求完成下列各题。
1. 用8,3,7,0,0,0,0组成一个七位数。(每种情况只写一个数)
(1)只读一个零的数:______________________________。
(2)读两个零的数:______________________________。
(3)一个零都不读的数:______________________________。
(4)与7000000最接近的数:____________________________。
(5)万位上的数字是0的最大七位数:______________________。
8000037
8000307
8003700
7000038
8703000
(前3小题答案不唯一)
2. 读出下面横线上的数。
(1)俄罗斯的国土面积大约是17098200平方千米。
读作:______________________________
(2)日本的国土面积大约是378000平方千米。
读作:______________________________
(3)美国的国土面积大约是9629091平方千米。
读作:______________________________
一千七百零九万八千二百
三十七万八千
九百六十二万九千零九十一
四 解决问题。
1. 一个四位数,它的十位上的数字是6,百位上的数比十位上的数少3,千位上的数比十位上的数多1,个位上是最大的一位数,这个数是多少?
百位上的数是6-3=3,千位上的数是6+1=7,
最大的一位数是9。
答:这个数是7369。
2. 同学们排队做操,不论是每行8人,还是每行10人,或是每行12人,最后都正好多出5人。至少有多少人做操
8,10,12的最小公倍数是120,
120+5=125(人)
答:至少有125人做操。
3. 要把它们截成同样长的小棒,不能有剩余,每根小棒最长是多少厘米?
32=2×2×2×2×248=2×2×2×2×3
所以32和48的最大公因数是2×2×2×2=16,
即每根小棒最长是16 cm。
答:每根小棒最长是16 cm。
同课章节目录
