数学人教A版(2019)选择性必修第一册2.1.1直线的倾斜角与斜率(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1直线的倾斜角与斜率(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 611.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 19:40:30 | ||
图片预览




文档简介
(共17张PPT)
聚焦核心素养的大单元课堂教学
探究
人民教育出版社A 版 普通高中教科书 《数学》 选择性必修 第一册
第二章 直线和圆的方程
揭示课题
万物皆变
描述运动变化现 象
把握运动变化规律
精确刻画运动轨迹
勒内 · 笛卡尔
(公元1596 年 3 月 31 日—公元1650 年 2 月 11 日)
皮耶 · 德 · 费 马 (公元 1601 年 8 月 17 日—公元 1665 年1 月12 日)
解析几何
x
y
o
P(x, y)
坐 标 法
综 合 法
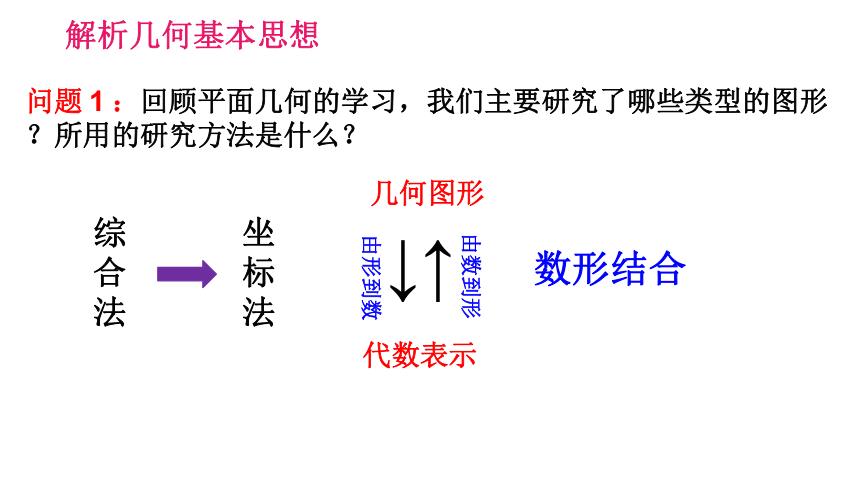
解析几何基本思想
问题 1 :回顾平面几何的学习,我们主要研究了哪些类型的图形
?所用的研究方法是什么?
几何图形
↓↑
代数表示
由形到数
由数到形
数形结合
聚焦核心素养的大单元课堂教学
探究
人民教育出版社A 版 普通高中教科书 《数学》 选择性必修 第一册
第二章 直线和圆的方程
2.1.1 直线的倾斜角与斜率
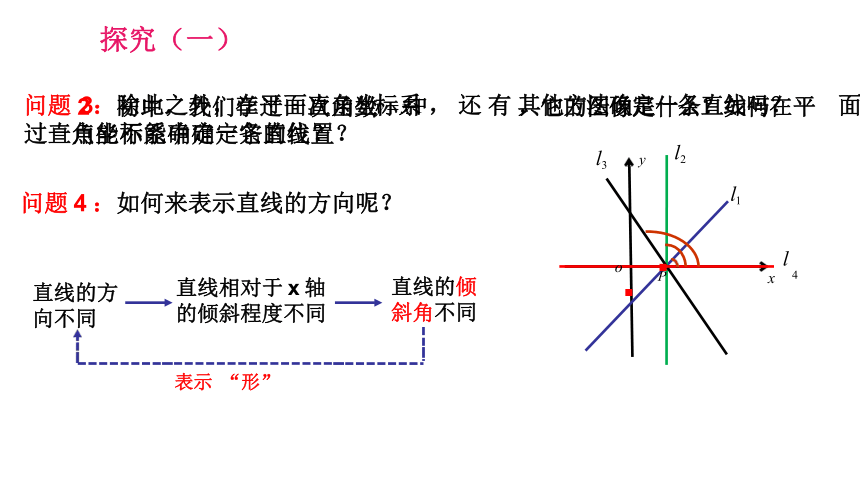
问题 4 :如何来表示直线的方向呢?
问题 23 :初除中此,之我外,们学在过平一面次直角函数坐y标 系 x 中 1 , 还 有 其,他它方的法图确像定是一什条么直?线如吗何?在平 面过一直角点能坐标不系能确中确定一定它条的直位线置??
直线的方 向不同
直线的倾 斜角不同
探究(一)
直线相对于 x 轴 的倾斜程度不同
表示 “形”
y
o. .P
l1
l2
l3
l
x 4
1. 倾斜角:
.
问题 5 :直线的倾斜角在什么范围内变化
?
概念生成
y
当直线 l 与x 轴相交时,我们以x 轴为基准x , 轴正向与直l 线 向上的方向
[0 , 180 )
o
o
x
y
o
P
之间所成的α 角 叫做l 直线 的倾斜角 .
规定:当直线 l 与x 轴平行或重合时,它的倾斜角为00
l
l
l
l
y
x
o
x
o
y
x
o
y
x
o
α (00 ,900 )
α 900
α (900 ,1800 )
α 00
o
x
y
P
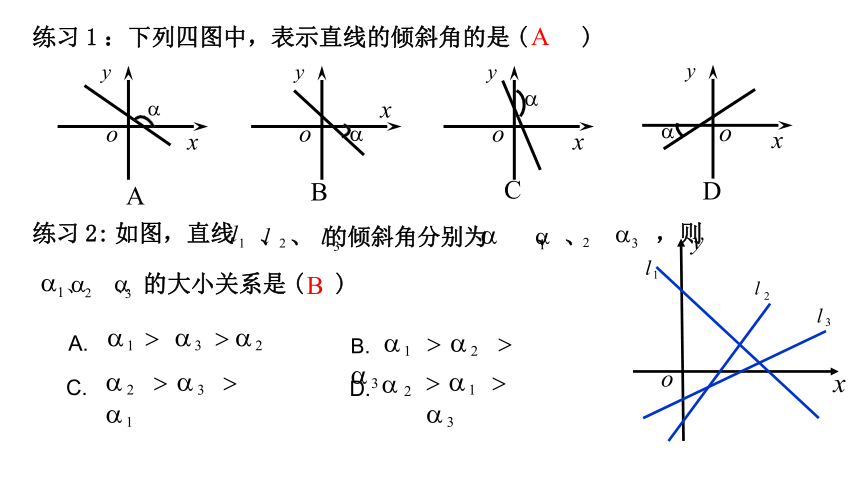
练习 1 :下列四图中,表示直线的倾斜角的是 ( A )
B
C
D
,则
1 、 2 、 3 的大小关系是 ( B )
A.
C.
B. 1 2 3
D. 2
x
x
o o
y y y
x
o
A
练习 2: 如图,直线l
y
x
o
1 2
3
l
1
2
、l 、 的倾斜角分别为 、 、
3
l1
2
l
l3
x
y
o
1 3 2
2 3 1
1 3
想一想
下列说法正确吗?
所有的直线都有唯一确定的倾斜角与之对应 .
每一个倾斜角都对应于唯一确定的一条直线 .
.
x
l1
y
o
.l2
α
探究(二)
问题 6 :两点P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) 唯一确l 定一条直线l ,此时直α 线P 1 , P2 的倾斜角 与 两点的坐标有怎样的关系?
知直线 经过 l O (0 , 0 ), P ( 3 ,1 ) α ,O , 与P 的坐标有什么关系?
x
y
o
P( 3.,1)
α
3
tan α 1
1
2
sin α
2
3 0
1 0
( 3 0)2 (1 0)2
3
cos α 3
( 3 0)2 (1 0)2
1
探究(二)
.
直线 经过 l P 1 ( 1 ,1 ) , P 2 (2 , 0 ) α , P1 ,与P2 的坐标又有什么关系?
x
y
o
tan α 1
P1 ( 1,1)
2
P ( 2,0)
P
OP P2 P1 ( 1 2,1)
P( 1 2,1)
α α
1 2 1 2
1 0
( 1 2)2 12
sin α 1
1 2
( 1 2)2 12
cos α
探究(二)
x
o
α
直 线 经 过 l P 1 ( x 1 , y 1 ), P 2 (x 2 , y 2 ) x,1 x 2 α ,P1 , P 2 与 的 坐 标 有 什 么
x
y y
o
x
y
o
x
y
o
α
α
P1
P2
P2
P1
P2
x
y
o
P1
P2
x
y
o
P1
P2
P1
α
P2 P1
练习 3 :如图,已知A ( 1 ,0 ) , B ( 0 , 1 ) ,求直线A B 的倾 斜角 .
解设:直线 A B 的倾斜角分别为 α , 则
结论
问题 7 :公式的意义是什么?
形
倾斜角
数
斜率
1 ( 1)
tan α 1
1 0
4
α π
x
y
o
A
B
1 2
y1 y1 y2
tan α y2
(x x )
2 1 1 2
x x x x
α
x
y
o
P1
P2
讨思论考:所当有直线的都倾有斜角率由吗 ?0 0 逐渐增加到18 0 0 时,其斜率如何变
化?为什么?并完成表格 .
想一想
k tan α
探究(三)
2. 斜率:
我们把一条直线倾斜角α 的正切值叫做这条直线的斜率 . 斜率常用小 写字母k 表示,即
α [00 ,900 ) (900 ,1800 )
8 :如果直线经过两点 P1 (x 1 , y 1 ), P 2 (x 2 , y 2 ) ,求该直线的斜率 .
.
.
锐角
钝角
x2 x1
y2 y1
tan α
k tan α
x x
2
(x1 x )
2 1 1 2
x x
y1 y1 y2
k y2
α
x
y
o
1
P .
P.2
例 1 已 知 A ( 3 ,2 ) , B ( 4 ,1 ), C ( 0 , 1 ) A B , B C , 求 直线 的斜率,并判断它们的倾斜角是锐角还
A.
B
C
4 3 7
AB
是钝角? k 1 2 1
1 1 1
0
0 ( 4) 2
kBC
0
课堂小结
方法
坐标法
知识
直线的倾斜 角与斜率
思想 数形结合 分类讨论
探究
结合斜率的计算公式,探讨直线的方向向量与斜率之间的关系 .
方向向量
(1)
LOREM IPSUM
x
y
o
P1
P2
1
x2 x1
y
k y2
k
(x, y)
(2) 方向向量
v
(x1 x2 )
(x 0)
v
P1P2 (x2 x1 , y2 y1 )
k
聚焦核心素养的大单元课堂教学
探究
人民教育出版社A 版 普通高中教科书 《数学》 选择性必修 第一册
第二章 直线和圆的方程
揭示课题
万物皆变
描述运动变化现 象
把握运动变化规律
精确刻画运动轨迹
勒内 · 笛卡尔
(公元1596 年 3 月 31 日—公元1650 年 2 月 11 日)
皮耶 · 德 · 费 马 (公元 1601 年 8 月 17 日—公元 1665 年1 月12 日)
解析几何
x
y
o
P(x, y)
坐 标 法
综 合 法
解析几何基本思想
问题 1 :回顾平面几何的学习,我们主要研究了哪些类型的图形
?所用的研究方法是什么?
几何图形
↓↑
代数表示
由形到数
由数到形
数形结合
聚焦核心素养的大单元课堂教学
探究
人民教育出版社A 版 普通高中教科书 《数学》 选择性必修 第一册
第二章 直线和圆的方程
2.1.1 直线的倾斜角与斜率
问题 4 :如何来表示直线的方向呢?
问题 23 :初除中此,之我外,们学在过平一面次直角函数坐y标 系 x 中 1 , 还 有 其,他它方的法图确像定是一什条么直?线如吗何?在平 面过一直角点能坐标不系能确中确定一定它条的直位线置??
直线的方 向不同
直线的倾 斜角不同
探究(一)
直线相对于 x 轴 的倾斜程度不同
表示 “形”
y
o. .P
l1
l2
l3
l
x 4
1. 倾斜角:
.
问题 5 :直线的倾斜角在什么范围内变化
?
概念生成
y
当直线 l 与x 轴相交时,我们以x 轴为基准x , 轴正向与直l 线 向上的方向
[0 , 180 )
o
o
x
y
o
P
之间所成的α 角 叫做l 直线 的倾斜角 .
规定:当直线 l 与x 轴平行或重合时,它的倾斜角为00
l
l
l
l
y
x
o
x
o
y
x
o
y
x
o
α (00 ,900 )
α 900
α (900 ,1800 )
α 00
o
x
y
P
练习 1 :下列四图中,表示直线的倾斜角的是 ( A )
B
C
D
,则
1 、 2 、 3 的大小关系是 ( B )
A.
C.
B. 1 2 3
D. 2
x
x
o o
y y y
x
o
A
练习 2: 如图,直线l
y
x
o
1 2
3
l
1
2
、l 、 的倾斜角分别为 、 、
3
l1
2
l
l3
x
y
o
1 3 2
2 3 1
1 3
想一想
下列说法正确吗?
所有的直线都有唯一确定的倾斜角与之对应 .
每一个倾斜角都对应于唯一确定的一条直线 .
.
x
l1
y
o
.l2
α
探究(二)
问题 6 :两点P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) 唯一确l 定一条直线l ,此时直α 线P 1 , P2 的倾斜角 与 两点的坐标有怎样的关系?
知直线 经过 l O (0 , 0 ), P ( 3 ,1 ) α ,O , 与P 的坐标有什么关系?
x
y
o
P( 3.,1)
α
3
tan α 1
1
2
sin α
2
3 0
1 0
( 3 0)2 (1 0)2
3
cos α 3
( 3 0)2 (1 0)2
1
探究(二)
.
直线 经过 l P 1 ( 1 ,1 ) , P 2 (2 , 0 ) α , P1 ,与P2 的坐标又有什么关系?
x
y
o
tan α 1
P1 ( 1,1)
2
P ( 2,0)
P
OP P2 P1 ( 1 2,1)
P( 1 2,1)
α α
1 2 1 2
1 0
( 1 2)2 12
sin α 1
1 2
( 1 2)2 12
cos α
探究(二)
x
o
α
直 线 经 过 l P 1 ( x 1 , y 1 ), P 2 (x 2 , y 2 ) x,1 x 2 α ,P1 , P 2 与 的 坐 标 有 什 么
x
y y
o
x
y
o
x
y
o
α
α
P1
P2
P2
P1
P2
x
y
o
P1
P2
x
y
o
P1
P2
P1
α
P2 P1
练习 3 :如图,已知A ( 1 ,0 ) , B ( 0 , 1 ) ,求直线A B 的倾 斜角 .
解设:直线 A B 的倾斜角分别为 α , 则
结论
问题 7 :公式的意义是什么?
形
倾斜角
数
斜率
1 ( 1)
tan α 1
1 0
4
α π
x
y
o
A
B
1 2
y1 y1 y2
tan α y2
(x x )
2 1 1 2
x x x x
α
x
y
o
P1
P2
讨思论考:所当有直线的都倾有斜角率由吗 ?0 0 逐渐增加到18 0 0 时,其斜率如何变
化?为什么?并完成表格 .
想一想
k tan α
探究(三)
2. 斜率:
我们把一条直线倾斜角α 的正切值叫做这条直线的斜率 . 斜率常用小 写字母k 表示,即
α [00 ,900 ) (900 ,1800 )
8 :如果直线经过两点 P1 (x 1 , y 1 ), P 2 (x 2 , y 2 ) ,求该直线的斜率 .
.
.
锐角
钝角
x2 x1
y2 y1
tan α
k tan α
x x
2
(x1 x )
2 1 1 2
x x
y1 y1 y2
k y2
α
x
y
o
1
P .
P.2
例 1 已 知 A ( 3 ,2 ) , B ( 4 ,1 ), C ( 0 , 1 ) A B , B C , 求 直线 的斜率,并判断它们的倾斜角是锐角还
A.
B
C
4 3 7
AB
是钝角? k 1 2 1
1 1 1
0
0 ( 4) 2
kBC
0
课堂小结
方法
坐标法
知识
直线的倾斜 角与斜率
思想 数形结合 分类讨论
探究
结合斜率的计算公式,探讨直线的方向向量与斜率之间的关系 .
方向向量
(1)
LOREM IPSUM
x
y
o
P1
P2
1
x2 x1
y
k y2
k
(x, y)
(2) 方向向量
v
(x1 x2 )
(x 0)
v
P1P2 (x2 x1 , y2 y1 )
k
