北师大版 五年级数学下册 -2.(长方体)同步作业 (含答案)
文档属性
| 名称 | 北师大版 五年级数学下册 -2.(长方体)同步作业 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 107.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 08:37:05 | ||
图片预览




文档简介
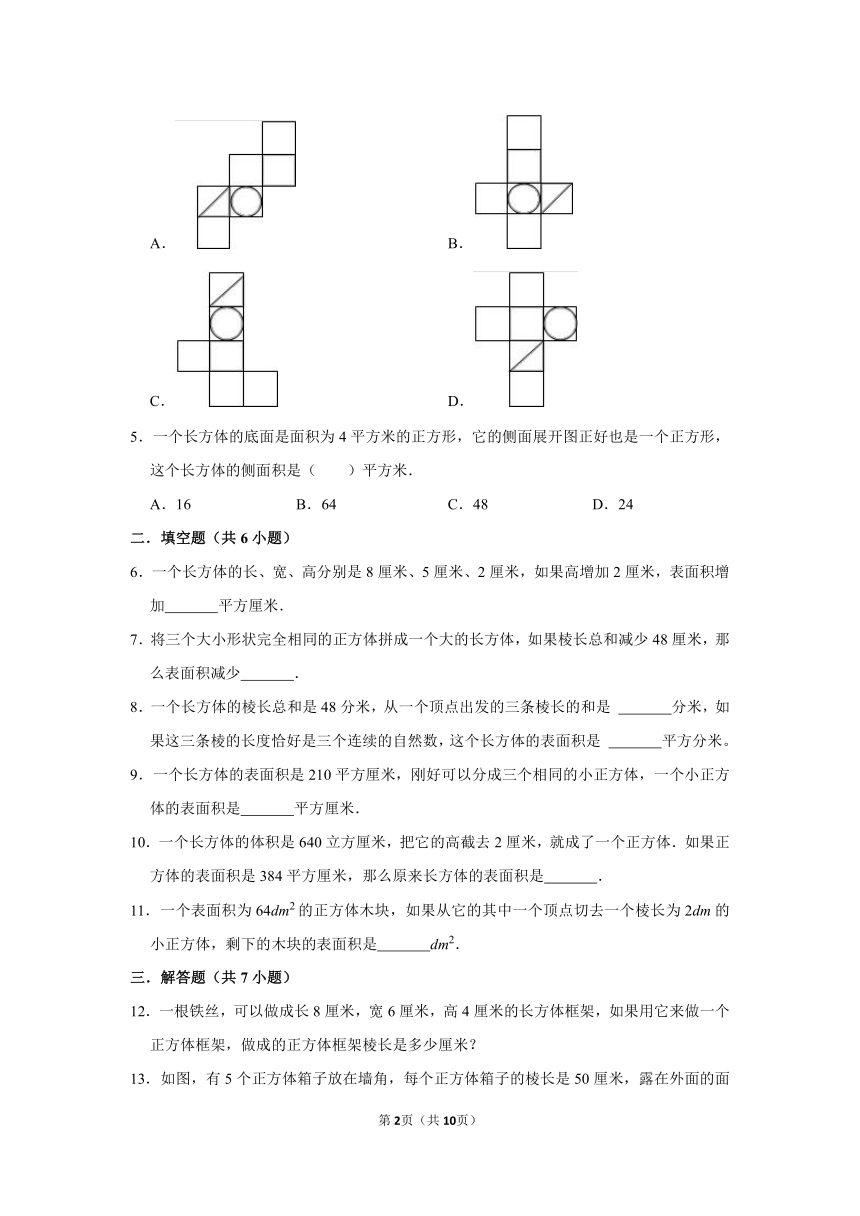
同步作业-2.(长方体)-2021-2022学年下学期小学数学北师大版五年级
一.选择题(共5小题)
1.下面图形中,不是正方体展开图的是( )
A. B.
C. D.
2.从一个长方体木块中,挖掉两小块后(如图)。它的表面积( )
A.和原来同样大 B.比原来小
C.比原来大
3.将一摞练习本摆成长方体,再均匀地斜放(如图),从前面看,由长方形变成一个近似的平行四边形.长方形和近似平行四边形相比,( )
A.周长和面积都不变 B.周长和面积都变了
C.周长不变,面积变小 D.周长变大,面积不变
4.如图所示的立方体,如果把它展开,可以是下列图形中的( )
A. B.
C. D.
5.一个长方体的底面是面积为4平方米的正方形,它的侧面展开图正好也是一个正方形,这个长方体的侧面积是( )平方米.
A.16 B.64 C.48 D.24
二.填空题(共6小题)
6.一个长方体的长、宽、高分别是8厘米、5厘米、2厘米,如果高增加2厘米,表面积增加 平方厘米.
7.将三个大小形状完全相同的正方体拼成一个大的长方体,如果棱长总和减少48厘米,那么表面积减少 .
8.一个长方体的棱长总和是48分米,从一个顶点出发的三条棱长的和是 分米,如果这三条棱的长度恰好是三个连续的自然数,这个长方体的表面积是 平方分米。
9.一个长方体的表面积是210平方厘米,刚好可以分成三个相同的小正方体,一个小正方体的表面积是 平方厘米.
10.一个长方体的体积是640立方厘米,把它的高截去2厘米,就成了一个正方体.如果正方体的表面积是384平方厘米,那么原来长方体的表面积是 .
11.一个表面积为64dm2的正方体木块,如果从它的其中一个顶点切去一个棱长为2dm的小正方体,剩下的木块的表面积是 dm2.
三.解答题(共7小题)
12.一根铁丝,可以做成长8厘米,宽6厘米,高4厘米的长方体框架,如果用它来做一个正方体框架,做成的正方体框架棱长是多少厘米?
13.如图,有5个正方体箱子放在墙角,每个正方体箱子的棱长是50厘米,露在外面的面积是多少?
14.用丝带捆扎一个长25cm,宽20cm,高10cm的长方体礼盒.打结处长40cm.捆扎这个礼盒至少需要多少长的丝带?
15.有两个完全一样的长方体,它们的长、宽、高分别是8厘米、6厘米、4厘米.把这两个长方体拼成一个新的长方体,这个长方体的表面积最大是多少平方厘米?最小是多少平方厘米?
16.“淘宝之父”马云新出了两本大小相同的书,长都为20厘米、宽为12厘米、厚3厘米,将这两本书包装在一起,怎样包装最省纸?请画出示意图,并算出包装纸的面积.(接头处不计)
17.一个正方体木块棱长10厘米,在每个面的中央各挖掉一个洞,洞口是边长3厘米的正方形,洞深3厘米.挖好后的木块表面积是多少?
18.一块长方形铁皮(如图),从四个角各切掉一个边长为5cm的正方形,然后做成盒子,这个盒子用了多少铁皮?
同步作业-2.(长方体)-2021-2022学年下学期小学数学北师大版五年级
参考答案与试题解析
一.选择题(共5小题)
1.【分析】正方体的十一种平面展开图可记忆口诀:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。据此解答。
【解答】解:根据口诀可知,一行有4个的,只能是一四一,所以备选答案C错误。
故选:C。
【点评】本题主要考查正方体的展开图,记住口诀是解本题的关键。
2.【分析】通过观察图形可知,顶点上的小正方体原来外露3个,从顶点上拿掉一个小正方体后,又外露与原来相同的3个面;从长方体棱的中间拿掉一个小正方体,这个小正方体原来外露2个面,拿掉之后比原来多外露2个面。由此可知,剩下图形的表面积比原来增加了小正方体的2个面的面积。据此解答。
【解答】解:由分析得:从顶点上拿掉一个小正方体后,表面积不变,从棱的中间拿掉一个小正方体后,表面积比原来增加了小正方体的2个面的面积。所以剩下图形的表面积比原来大。
故选:C。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用,关键是明确:从顶点上拿掉一个小正方体后,表面积不变,从棱的中间拿掉一个小正方体后,表面积比原来增加了小正方体的2个面的面积。
3.【分析】根据长方形和平行四边形的特征可知,把长方形拉成平行四边形,因为每本练习本的厚度不变,从前面看,由长方形变成一个近似的平行四边形后,底和高都不变,因此面积不变;把长方形拉成平行四边形,平行四边形的一组对边大于长方形的宽,所以周长变大。据此解答。
【解答】解:如图:
从前面看,由长方形变成一个近似的平行四边形,长方形和近似平行四边形相比周长变大,面积不变。
故选:D。
【点评】解决此题的关键是弄清:把一个长方形拉成一个平行四边形,围成长方形和平行四边形的四条边的长度变大,高度没变。
4.【分析】把正方体展开有四种情况:A是2﹣2﹣2型;B是1﹣4﹣1型;C是1﹣4﹣1型;D是1﹣4﹣1型,把这几个图形分别折成正方体,会发现三个阴影的面相邻,但又不在同一列上,而且直角三角形的锐角所在的顶点与呈正方形阴影的面共用一个顶点.只有d是上面正方体的展开图.据此判断.
【解答】解:由分析可知,如图所示的立方体,如果把它展开,是D;
故选:D.
【点评】解决此题的关键是分析展开图属于哪种类型,通过动手折回正方体找答案,注意其中一个面的斜线方向.
5.【分析】首先根据正方形的面积公式:S=a2,已知长方体的底面是面积为4平方米的正方形,据此可以求出长方体的底面边长,又知这个长方体的侧面展开是一个正方形,那么这个长方体的底面周长和高相等,根据正方形的周长公式:C=4a,求出底面周长,然后根据正方形的面积公式解答即可.
【解答】解:因为2的平方是4,所以底面边长是2米,
(2×4)×(2×4)
=8×8
=64(平方米),
答:这个长方体的侧面积是64平方米.
故选:B.
【点评】此题主要考查正方形的面积公式、正方形的周长公式的灵活运用,关键是熟记公式.
二.填空题(共6小题)
6.【分析】由题意可知:增加的表面积实际上就是高为2厘米的长方体的侧面积,于是利用侧面积=底面周长×高,代入数据即可求解.
【解答】解:(8+5)×2×2
=13×2×2
=52(平方厘米);
答:表面积增加52平方厘米.
故答案为:52.
【点评】解答此题的关键是:明白增加部分是一个什么样的图形,从而利用公式求解.
7.【分析】将三个大小形状完全相同的正方体拼成一个大的长方体,减少了4个正方体的面,减少了16个正方体的棱长,由于棱长总和减少48厘米,依此可求正方体的棱长,再根据正方形的面积公式可得一个面的面积,再乘以4即可求解.
【解答】解:48÷16=3(厘米)
3×3×4
=9×4
=36(平方厘米)
答:表面积减少了36平方厘米.
故答案为:36平方厘米.
【点评】考查了长方体和正方体的表面积,本题关键是得到正方体的棱长.
8.【分析】根据长方体的棱长总和=(长+宽+高)×4,那么长、宽、高的和=棱长总和÷4,再根据自然数的排列规律,相邻的两个自然数相差1,据此可以求出这个长方体的长、宽、高,然后根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:48÷4=12(分米)
12÷3=4(分米)
4﹣1=3(分米)
4+1=5(分米)
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方分米)
答:从一个顶点出发的三条棱长的和是12分米,这个长方体的表面积是94平方分米。
故答案为:12,94。
【点评】此题主要考查长方体的棱长总和公式、表面积公式的灵活运用,自然数的排列规律及应用,关键是求出长方体的长、宽、高。
9.【分析】把长方体平均分开,正好成为三个相同的正方体,也就是说,长方体的表面积是一个正方体14个面的面积,先求出正方体一个面的面积,每个正方体的表面积即可求出.
【解答】解:正方体一个面的面积为:
210÷14=15(平方厘米);
所以一个小正方体的表面积是:
15×6=90(平方厘米);
答:一个小正方体的表面积是90平方厘米.
故答案为:90.
【点评】本题考查对长方体和正方体表面积的计算能力,以及空间分析与想象能力.
10.【分析】正方体的表面积已知,利用正方体的表面积S=6a2,先求出正方体的每个面的面积,也就等于知道了长方体的底面积,从而可以求出每个面的长和宽(长和宽相等),长方体的体积已知,利用长方体的体积V=Sh即可求出长方体的高,再利用长方体的表面积S=(ab+bh+ah)×2,即可求出这个长方体的表面积.
【解答】解:384÷6=64(平方厘米),
又因8×8=64,
所以长方体的长和宽都是8厘米,
640÷64=10(厘米),
(8×8+8×10+10×8)×2,
=(64+80+80)×2,
=448(平方厘米);
答:原来长方体的表面积是448平方厘米.
故答案为:448平方厘米.
【点评】此题主要考查长方体和正方体的表面积和体积的计算方法,关键是要求出长方体的长、宽、高.
11.【分析】将原正方体切去一个小正方体后,减少的表面积正好被新增加的表面积所补充,因此新的立体图形的表面积就等于原正方体的表面积,据此解答.
【解答】解:将原正方体切去一个小正方体后,减少的表面积正好被新增加的表面积所补充,因此新的立体图形的表面积就等于原正方体的表面积;
所以剩下的木块的表面积是64平方分米.
故答案为:64.
【点评】解答此题的关键是明确新立体图形的表面积就等于原正方体的表面积.
三.解答题(共7小题)
12.【分析】首先根据长方体的棱长总和=(长+宽+高)×4,求出这个长方体的棱长总和,再根据正方体的棱长总和=棱长×12,用棱长总和除以12即可求出正方体的棱长.
【解答】解:(8+6+4)×4÷12,
=18×4÷12,
=6(厘米),
答:做成的正方体框架棱长是6厘米.
【点评】此题考查的目的是掌握长方体、正方体的特征以及它们的棱长总和公式.
13.【分析】根据图形可知:上面外露3个正方形的面、前面外露5个正方形的面,右面外露两个正方形的面,根据正方形的面积公式:S=a2,把数据代入公式解答即可.
【解答】解:50×50×(3+5+2)
=2500×10
=25000(平方厘米)
答:露在外面的面积是25000平方厘米.
【点评】此题考查的目的是理解掌握正方体表面积的意义,以及正方形面积公式的灵活运用.
14.【分析】根据题意和图形可知,所需彩带的长度等于两条长+两条宽+4条高+打结用的长度,由此列式解答.
【解答】解:25×2+20×2+10×4+40
=50+40+40+40
=170(厘米),
答:捆扎这个礼品盒至少需要170厘米长的丝带.
【点评】此题属于长方体的棱长总和的实际应用,解答关键是弄清是如何捆扎的,也就是弄清是求哪些棱的长度和.
15.【分析】要使拼成长方体的表面积最大,也就是两个长方体的最小面(6×4)结合在一起,要使拼成长方体的最小,也就是两个长方体的最大面(8×6)结合在一起,拼成长方体的表面积比原来两个长方体的表面积和减少了两个结合面的面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答.
【解答】解:表面积最大是:
(8×6+8×4+6×4)×2×2﹣6×4×2
=(48+32+24)×2×2﹣24×2
=104×2×2﹣48
=416﹣48
=368(平方厘米);
表面积最小是:
(8×6+8×4+6×4)×2×2﹣8×6×2
=(48+32+24)×2×2﹣48×2
=104×2×2﹣96
=416﹣96
=320(平方厘米);
答:这个长方体的表面积最大是368平方厘米、最小是320平方厘米.
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式.
16.【分析】把这两个长方体书的20×12的面相粘合,得到的大长方体的表面积最小,比原来两个长方体书的表面积减少了2个最大的面,最节约包装纸,组成的长方体长20厘米,宽12厘米,高6厘米,由此即可解答.
【解答】解:如图所示:
(20×12+20×6+12×6)×2
=432×2
=864(平方厘米)
答:包装纸的面积是864平方厘米.
【点评】解决本题关键是了解三种不同的包装方法,找出减少了哪些面,由此求解.
17.【分析】根据题意可知:这个挖洞后木块的表面积等于大正方体的表面积,加上6个棱长为3厘米的小正方体的4个侧面的面积.
【解答】解:10×10×6+3×3×4×6
=600+216
=816(平方厘米)
答:挖洞后木块的表面积是816平方厘米.
【点评】此题考查不规则立体图形的表面积的计算方法,解决此题的关键是弄清楚挖好后的木块表面积有哪些面组成.
18.【分析】根据长方形的面积公式S=ab和正方形的面积公式S=a2求出长方形和正方形的面积,这个盒子用的铁皮的面积是这个长方形的面积减去4个边长为5厘米的小正方形的面积,据此即可解答.
【解答】解:40×30﹣5×5×4
=1200﹣100
=1100(cm2);
答:这个盒子用了1100cm2的铁皮.
【点评】本考查了长方形和正方形面积公式的灵活应用.
第1页(共3页)
一.选择题(共5小题)
1.下面图形中,不是正方体展开图的是( )
A. B.
C. D.
2.从一个长方体木块中,挖掉两小块后(如图)。它的表面积( )
A.和原来同样大 B.比原来小
C.比原来大
3.将一摞练习本摆成长方体,再均匀地斜放(如图),从前面看,由长方形变成一个近似的平行四边形.长方形和近似平行四边形相比,( )
A.周长和面积都不变 B.周长和面积都变了
C.周长不变,面积变小 D.周长变大,面积不变
4.如图所示的立方体,如果把它展开,可以是下列图形中的( )
A. B.
C. D.
5.一个长方体的底面是面积为4平方米的正方形,它的侧面展开图正好也是一个正方形,这个长方体的侧面积是( )平方米.
A.16 B.64 C.48 D.24
二.填空题(共6小题)
6.一个长方体的长、宽、高分别是8厘米、5厘米、2厘米,如果高增加2厘米,表面积增加 平方厘米.
7.将三个大小形状完全相同的正方体拼成一个大的长方体,如果棱长总和减少48厘米,那么表面积减少 .
8.一个长方体的棱长总和是48分米,从一个顶点出发的三条棱长的和是 分米,如果这三条棱的长度恰好是三个连续的自然数,这个长方体的表面积是 平方分米。
9.一个长方体的表面积是210平方厘米,刚好可以分成三个相同的小正方体,一个小正方体的表面积是 平方厘米.
10.一个长方体的体积是640立方厘米,把它的高截去2厘米,就成了一个正方体.如果正方体的表面积是384平方厘米,那么原来长方体的表面积是 .
11.一个表面积为64dm2的正方体木块,如果从它的其中一个顶点切去一个棱长为2dm的小正方体,剩下的木块的表面积是 dm2.
三.解答题(共7小题)
12.一根铁丝,可以做成长8厘米,宽6厘米,高4厘米的长方体框架,如果用它来做一个正方体框架,做成的正方体框架棱长是多少厘米?
13.如图,有5个正方体箱子放在墙角,每个正方体箱子的棱长是50厘米,露在外面的面积是多少?
14.用丝带捆扎一个长25cm,宽20cm,高10cm的长方体礼盒.打结处长40cm.捆扎这个礼盒至少需要多少长的丝带?
15.有两个完全一样的长方体,它们的长、宽、高分别是8厘米、6厘米、4厘米.把这两个长方体拼成一个新的长方体,这个长方体的表面积最大是多少平方厘米?最小是多少平方厘米?
16.“淘宝之父”马云新出了两本大小相同的书,长都为20厘米、宽为12厘米、厚3厘米,将这两本书包装在一起,怎样包装最省纸?请画出示意图,并算出包装纸的面积.(接头处不计)
17.一个正方体木块棱长10厘米,在每个面的中央各挖掉一个洞,洞口是边长3厘米的正方形,洞深3厘米.挖好后的木块表面积是多少?
18.一块长方形铁皮(如图),从四个角各切掉一个边长为5cm的正方形,然后做成盒子,这个盒子用了多少铁皮?
同步作业-2.(长方体)-2021-2022学年下学期小学数学北师大版五年级
参考答案与试题解析
一.选择题(共5小题)
1.【分析】正方体的十一种平面展开图可记忆口诀:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。据此解答。
【解答】解:根据口诀可知,一行有4个的,只能是一四一,所以备选答案C错误。
故选:C。
【点评】本题主要考查正方体的展开图,记住口诀是解本题的关键。
2.【分析】通过观察图形可知,顶点上的小正方体原来外露3个,从顶点上拿掉一个小正方体后,又外露与原来相同的3个面;从长方体棱的中间拿掉一个小正方体,这个小正方体原来外露2个面,拿掉之后比原来多外露2个面。由此可知,剩下图形的表面积比原来增加了小正方体的2个面的面积。据此解答。
【解答】解:由分析得:从顶点上拿掉一个小正方体后,表面积不变,从棱的中间拿掉一个小正方体后,表面积比原来增加了小正方体的2个面的面积。所以剩下图形的表面积比原来大。
故选:C。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用,关键是明确:从顶点上拿掉一个小正方体后,表面积不变,从棱的中间拿掉一个小正方体后,表面积比原来增加了小正方体的2个面的面积。
3.【分析】根据长方形和平行四边形的特征可知,把长方形拉成平行四边形,因为每本练习本的厚度不变,从前面看,由长方形变成一个近似的平行四边形后,底和高都不变,因此面积不变;把长方形拉成平行四边形,平行四边形的一组对边大于长方形的宽,所以周长变大。据此解答。
【解答】解:如图:
从前面看,由长方形变成一个近似的平行四边形,长方形和近似平行四边形相比周长变大,面积不变。
故选:D。
【点评】解决此题的关键是弄清:把一个长方形拉成一个平行四边形,围成长方形和平行四边形的四条边的长度变大,高度没变。
4.【分析】把正方体展开有四种情况:A是2﹣2﹣2型;B是1﹣4﹣1型;C是1﹣4﹣1型;D是1﹣4﹣1型,把这几个图形分别折成正方体,会发现三个阴影的面相邻,但又不在同一列上,而且直角三角形的锐角所在的顶点与呈正方形阴影的面共用一个顶点.只有d是上面正方体的展开图.据此判断.
【解答】解:由分析可知,如图所示的立方体,如果把它展开,是D;
故选:D.
【点评】解决此题的关键是分析展开图属于哪种类型,通过动手折回正方体找答案,注意其中一个面的斜线方向.
5.【分析】首先根据正方形的面积公式:S=a2,已知长方体的底面是面积为4平方米的正方形,据此可以求出长方体的底面边长,又知这个长方体的侧面展开是一个正方形,那么这个长方体的底面周长和高相等,根据正方形的周长公式:C=4a,求出底面周长,然后根据正方形的面积公式解答即可.
【解答】解:因为2的平方是4,所以底面边长是2米,
(2×4)×(2×4)
=8×8
=64(平方米),
答:这个长方体的侧面积是64平方米.
故选:B.
【点评】此题主要考查正方形的面积公式、正方形的周长公式的灵活运用,关键是熟记公式.
二.填空题(共6小题)
6.【分析】由题意可知:增加的表面积实际上就是高为2厘米的长方体的侧面积,于是利用侧面积=底面周长×高,代入数据即可求解.
【解答】解:(8+5)×2×2
=13×2×2
=52(平方厘米);
答:表面积增加52平方厘米.
故答案为:52.
【点评】解答此题的关键是:明白增加部分是一个什么样的图形,从而利用公式求解.
7.【分析】将三个大小形状完全相同的正方体拼成一个大的长方体,减少了4个正方体的面,减少了16个正方体的棱长,由于棱长总和减少48厘米,依此可求正方体的棱长,再根据正方形的面积公式可得一个面的面积,再乘以4即可求解.
【解答】解:48÷16=3(厘米)
3×3×4
=9×4
=36(平方厘米)
答:表面积减少了36平方厘米.
故答案为:36平方厘米.
【点评】考查了长方体和正方体的表面积,本题关键是得到正方体的棱长.
8.【分析】根据长方体的棱长总和=(长+宽+高)×4,那么长、宽、高的和=棱长总和÷4,再根据自然数的排列规律,相邻的两个自然数相差1,据此可以求出这个长方体的长、宽、高,然后根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解答】解:48÷4=12(分米)
12÷3=4(分米)
4﹣1=3(分米)
4+1=5(分米)
(5×4+5×3+4×3)×2
=(20+15+12)×2
=47×2
=94(平方分米)
答:从一个顶点出发的三条棱长的和是12分米,这个长方体的表面积是94平方分米。
故答案为:12,94。
【点评】此题主要考查长方体的棱长总和公式、表面积公式的灵活运用,自然数的排列规律及应用,关键是求出长方体的长、宽、高。
9.【分析】把长方体平均分开,正好成为三个相同的正方体,也就是说,长方体的表面积是一个正方体14个面的面积,先求出正方体一个面的面积,每个正方体的表面积即可求出.
【解答】解:正方体一个面的面积为:
210÷14=15(平方厘米);
所以一个小正方体的表面积是:
15×6=90(平方厘米);
答:一个小正方体的表面积是90平方厘米.
故答案为:90.
【点评】本题考查对长方体和正方体表面积的计算能力,以及空间分析与想象能力.
10.【分析】正方体的表面积已知,利用正方体的表面积S=6a2,先求出正方体的每个面的面积,也就等于知道了长方体的底面积,从而可以求出每个面的长和宽(长和宽相等),长方体的体积已知,利用长方体的体积V=Sh即可求出长方体的高,再利用长方体的表面积S=(ab+bh+ah)×2,即可求出这个长方体的表面积.
【解答】解:384÷6=64(平方厘米),
又因8×8=64,
所以长方体的长和宽都是8厘米,
640÷64=10(厘米),
(8×8+8×10+10×8)×2,
=(64+80+80)×2,
=448(平方厘米);
答:原来长方体的表面积是448平方厘米.
故答案为:448平方厘米.
【点评】此题主要考查长方体和正方体的表面积和体积的计算方法,关键是要求出长方体的长、宽、高.
11.【分析】将原正方体切去一个小正方体后,减少的表面积正好被新增加的表面积所补充,因此新的立体图形的表面积就等于原正方体的表面积,据此解答.
【解答】解:将原正方体切去一个小正方体后,减少的表面积正好被新增加的表面积所补充,因此新的立体图形的表面积就等于原正方体的表面积;
所以剩下的木块的表面积是64平方分米.
故答案为:64.
【点评】解答此题的关键是明确新立体图形的表面积就等于原正方体的表面积.
三.解答题(共7小题)
12.【分析】首先根据长方体的棱长总和=(长+宽+高)×4,求出这个长方体的棱长总和,再根据正方体的棱长总和=棱长×12,用棱长总和除以12即可求出正方体的棱长.
【解答】解:(8+6+4)×4÷12,
=18×4÷12,
=6(厘米),
答:做成的正方体框架棱长是6厘米.
【点评】此题考查的目的是掌握长方体、正方体的特征以及它们的棱长总和公式.
13.【分析】根据图形可知:上面外露3个正方形的面、前面外露5个正方形的面,右面外露两个正方形的面,根据正方形的面积公式:S=a2,把数据代入公式解答即可.
【解答】解:50×50×(3+5+2)
=2500×10
=25000(平方厘米)
答:露在外面的面积是25000平方厘米.
【点评】此题考查的目的是理解掌握正方体表面积的意义,以及正方形面积公式的灵活运用.
14.【分析】根据题意和图形可知,所需彩带的长度等于两条长+两条宽+4条高+打结用的长度,由此列式解答.
【解答】解:25×2+20×2+10×4+40
=50+40+40+40
=170(厘米),
答:捆扎这个礼品盒至少需要170厘米长的丝带.
【点评】此题属于长方体的棱长总和的实际应用,解答关键是弄清是如何捆扎的,也就是弄清是求哪些棱的长度和.
15.【分析】要使拼成长方体的表面积最大,也就是两个长方体的最小面(6×4)结合在一起,要使拼成长方体的最小,也就是两个长方体的最大面(8×6)结合在一起,拼成长方体的表面积比原来两个长方体的表面积和减少了两个结合面的面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答.
【解答】解:表面积最大是:
(8×6+8×4+6×4)×2×2﹣6×4×2
=(48+32+24)×2×2﹣24×2
=104×2×2﹣48
=416﹣48
=368(平方厘米);
表面积最小是:
(8×6+8×4+6×4)×2×2﹣8×6×2
=(48+32+24)×2×2﹣48×2
=104×2×2﹣96
=416﹣96
=320(平方厘米);
答:这个长方体的表面积最大是368平方厘米、最小是320平方厘米.
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式.
16.【分析】把这两个长方体书的20×12的面相粘合,得到的大长方体的表面积最小,比原来两个长方体书的表面积减少了2个最大的面,最节约包装纸,组成的长方体长20厘米,宽12厘米,高6厘米,由此即可解答.
【解答】解:如图所示:
(20×12+20×6+12×6)×2
=432×2
=864(平方厘米)
答:包装纸的面积是864平方厘米.
【点评】解决本题关键是了解三种不同的包装方法,找出减少了哪些面,由此求解.
17.【分析】根据题意可知:这个挖洞后木块的表面积等于大正方体的表面积,加上6个棱长为3厘米的小正方体的4个侧面的面积.
【解答】解:10×10×6+3×3×4×6
=600+216
=816(平方厘米)
答:挖洞后木块的表面积是816平方厘米.
【点评】此题考查不规则立体图形的表面积的计算方法,解决此题的关键是弄清楚挖好后的木块表面积有哪些面组成.
18.【分析】根据长方形的面积公式S=ab和正方形的面积公式S=a2求出长方形和正方形的面积,这个盒子用的铁皮的面积是这个长方形的面积减去4个边长为5厘米的小正方形的面积,据此即可解答.
【解答】解:40×30﹣5×5×4
=1200﹣100
=1100(cm2);
答:这个盒子用了1100cm2的铁皮.
【点评】本考查了长方形和正方形面积公式的灵活应用.
第1页(共3页)
