北师大版 五年级数学下册 2.(长方体)同步作业-(含答案)
文档属性
| 名称 | 北师大版 五年级数学下册 2.(长方体)同步作业-(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 84.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 00:00:00 | ||
图片预览



文档简介
(同步作业-2.(长方体)-2021-2022学年下学期小学数学北师大版五年级
一.选择题(共6小题)
1.如图,甲的表面积比乙的表面积( )
A.大 B.小 C.相等 D.无法确定
2.将四个长10cm,宽8cm,高3cm的长方体盒子,用彩纸包在一起,最省包装纸的方法是( )
A. B. C. D.
3.如果把一个长10cm、宽5cm、高5cm的长方体,切成两个完全一样的正方体,切成的两个正方体的表面积之和与原来长方体的表面积相比,( )
A.变大了 B.变小了 C.不变
4.把三个棱长是3cm的小正方体拼成一个长方体,长方体的表面积比三个小正方体的表面积之和少( )cm2。
A.27 B.54 C.36
5.一个长方体照如图沿虚线切三刀,切成若干个小长方体,这些小长方体的表面积之和比原来大长方体的表面积增加了90平方厘米。原来长方体的表面积是( )平方厘米。
A.30 B.90 C.180 D.270
6.如图是用棱长为2厘米的正方体摆成的物体,这个物体的表面积是( )平方厘米。
A.10 B.30 C.34 D.136
二.填空题(共5小题)
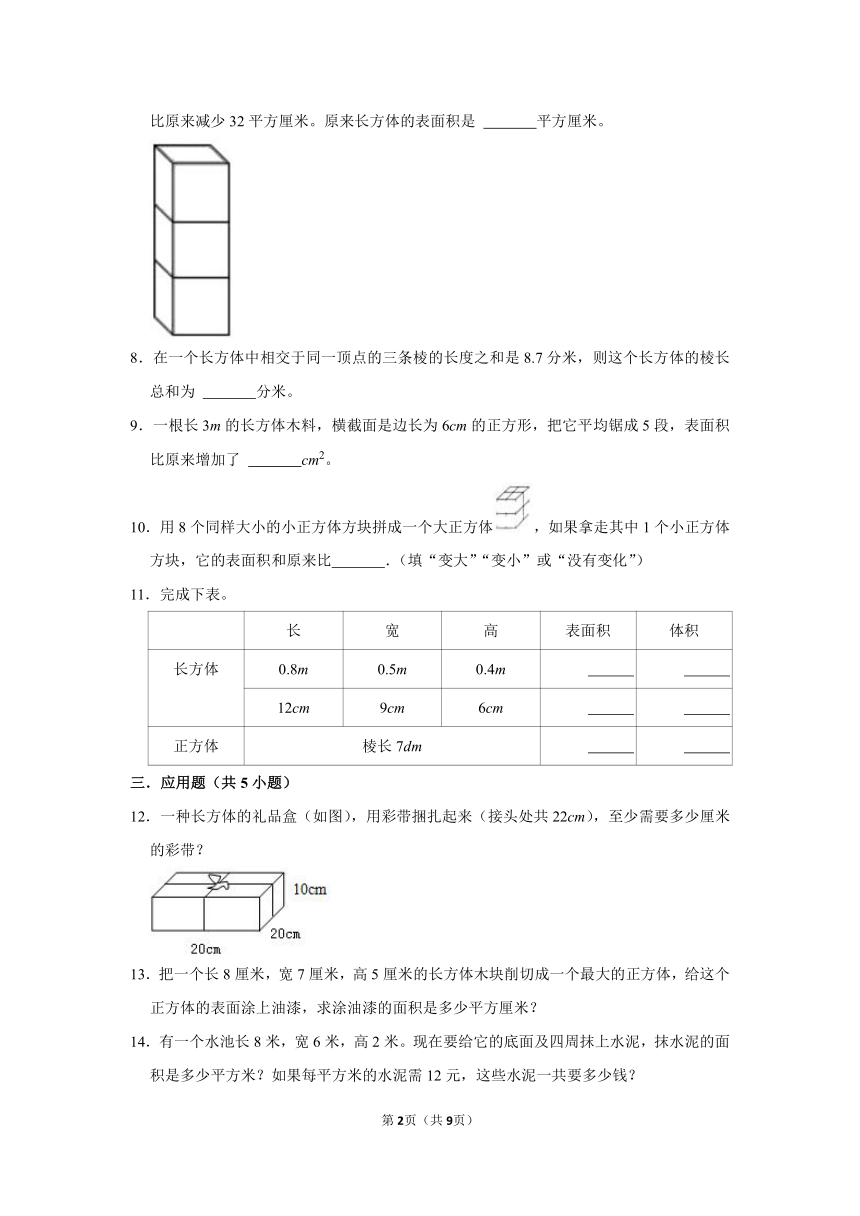
7.如图,一个长方体是由三个同样的正方体拼成的,如果去掉上面一个正方体,表面积就比原来减少32平方厘米。原来长方体的表面积是 平方厘米。
8.在一个长方体中相交于同一顶点的三条棱的长度之和是8.7分米,则这个长方体的棱长总和为 分米。
9.一根长3m的长方体木料,横截面是边长为6cm的正方形,把它平均锯成5段,表面积比原来增加了 cm2。
10.用8个同样大小的小正方体方块拼成一个大正方体,如果拿走其中1个小正方体方块,它的表面积和原来比 .(填“变大”“变小”或“没有变化”)
11.完成下表。
长 宽 高 表面积 体积
长方体 0.8m 0.5m 0.4m
12cm 9cm 6cm
正方体 棱长7dm
三.应用题(共5小题)
12.一种长方体的礼品盒(如图),用彩带捆扎起来(接头处共22cm),至少需要多少厘米的彩带?
13.把一个长8厘米,宽7厘米,高5厘米的长方体木块削切成一个最大的正方体,给这个正方体的表面涂上油漆,求涂油漆的面积是多少平方厘米?
14.有一个水池长8米,宽6米,高2米。现在要给它的底面及四周抹上水泥,抹水泥的面积是多少平方米?如果每平方米的水泥需12元,这些水泥一共要多少钱?
15.要粉刷教室的四壁及屋顶,教室长9米,宽6米,高3米,门窗的面积一共是21.7平方米,要粉刷的面积是多少平方米?如果每平方米用涂料0.5千克,一共要用涂料多少千克?
16.一块长28cm,宽24cm的长方形铁皮(如图),从四个角各切掉一个边长为4cm的正方形,然后做成盒子.这个盒子用了多少铁皮?
(同步作业-2.(长方体)-2021-2022学年下学期小学数学北师大版五年级
参考答案与试题解析
一.选择题(共6小题)
1.【分析】通过观察图形可知,乙图原来长方体顶点上的这个小正方体外露3个面,从顶点上挖掉1个小正方体后,又外露与原来相同的3个面,虽然体积减少了,但表面积不变。据此解答。
【解答】解:乙图原来长方体顶点上的这个小正方体外露3个面,从顶点上挖掉1个小正方体后,又外露与原来相同的3个面,虽然体积减少了,但表面积不变。
所以甲的表面积和乙的表面积相等。
故选:C。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用。
2.【分析】要想更省包装纸,需使表面积最小,由题意可知:只要求出哪种情况下,拼组后的大长方体的表面积与原来四个长方体的表面积之和相比,减少的面的面积最大,就最省包装纸。据此解答即可。
【解答】解:A、表面积减少了:(10×3+8×3)×4=54×4=216(平方厘米)
B、表面积减少了:10×8×6=80×6=480(平方厘米)
C、表面积减少了:(10×8+8×3)×4=104×4=416(平方厘米)
D、表面积减少了:(10×8+10×3)×4=110×4=440(平方厘米)
480>440>416>216
答:最省包装纸的方法是选项B。
故选:B。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用,关键是明确:要使拼组后的表面积最小,则把最大的面相粘合。
3.【分析】根据题意可知,把这个长方体切成两个完全一样的正方体,切成的两个正方体的表面积之和与原来长方体的表面积增加了两个切面的面积。据此解答。
【解答】解:如果把一个长10cm、宽5cm、高5cm的长方体,切成两个完全一样的正方体,切成的两个正方体的表面积之和与原来长方体的表面积相比变大了。
故选:A。
【点评】此题考查的目的是理解掌握长方体、正方体表面积的意义及应用。
4.【分析】根据题意可知,把三个棱长是3cm的小正方体拼成一个长方体,长方体的表面积比三个小正方体的表面积之和减少了正方体的4个面的面积,根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:3×3×4
=9×4
=36(平方厘米)
答:长方体的表面积比三个小正方体的表面积之和少36平方厘米。
故选:C。
【点评】此题考查的目的是理解掌握正方体、长方体表面积的意义,正方形面积公式的灵活运用,关键是熟记公式。
5.【分析】通过观察图形可知,与长方体的前后面平行切一刀增加的面积与前后面相同,同理:与上下面平行切一刀增加的面积与上下面相同;与左右面平行切一刀增加的面积与左右面相同,所以把这个长方体照如图沿虚线切三刀,这些小长方体的表面积之和比原来大长方体的表面积增加的面积就等于原来大长方体的表面积。据此解答即可。
【解答】解:与长方体的前后面平行切一刀增加的面积与前后面相同,同理:与上下面平行切一刀增加的面积与上下面相同;与左右面平行切一刀增加的面积与左右面相同,所以把这个长方体照如图沿虚线切三刀,这些小长方体的表面积之和比原来大长方体的表面积增加的面积就等于原来大长方体的表面积。
答:原来长方体的表面积是90平方厘米。
故选:B。
【点评】此题考查的目的是理解掌握长方体的特征,长方体表面积的意义及应用。
6.【分析】通过观察图形可知,前、后面都是正方体的5个面,上、下面都是正方体的7个面,左、右面都是正方体的5个面,根据正方形的面积公式:S=a2,求出正方体的一个面的面积,然后再乘这个组合图形外露的正方体的面的个数即可。
【解答】解:2×2×(5+7+5)×2
=4×17×2
=68×2
=136(平方厘米)
答:这个物体的表面积 136平方厘米。
故选:D。
【点评】此题主要考查正方体、长方体表面积公式的灵活运用,关键是弄清拼成组合图形的前后、上下、左右各外露多少个正方形的面。
二.填空题(共5小题)
7.【分析】根据题意可知,如果去掉上面一个正方体,表面积就比原来减少32平方厘米。表面积减少的是正方体的4个面的面积,据此可以求出正方体的一个面的面积,原来长方体的表面积等于正方体的14个面的面积。据此解答。
【解答】解:32÷4×14
=8×14
=112(平方厘米)
答:原来长方体的表面积是112平方厘米。
故答案为:112。
【点评】此题主要考查长方体、正方体表面积的意义及应用,关键是求出正方体的一个面的面积。
8.【分析】根据长方体的长、宽、高的意义,在长方体中相交于同一顶点的三条棱的长度分别叫做长方体的长、宽、高。在一个长方体中相交于同一顶点的三条棱的长度之和是8.7分米,也就是这个长方体的长、宽、高的和是8.7分米。再根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答。
【解答】解:8.7×4=34.8(分米)
答:这个长方体的棱长总和是34.8分米。
故答案为:34.8。
【点评】此题考查的目的是理解掌握长方体的特征,长方体棱长总和公式及应用。
9.【分析】根据题意可知,把这根木料平均锯成5段,需要锯4次,每锯一次就增加两个截面的面积,那么锯4次就增加8个截面的面积,根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:6×6×8
=36×8
=288(平方厘米)
答:表面积增加288平方厘米。
故答案为:288。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
10.【分析】因为在顶点处的小正方体外露3个面,拿掉一个小正方体后又外露与原来相同的3个面,所以表面积和原来相同.据此解答.
【解答】解:用8个同样大小的小正方体方块拼成一个大正方体,每个小正方体都在顶点上,因为在顶点处的小正方体外露3个面,拿掉一个小正方体后又外露与原来相同的3个面,所以表面积和原来相同.
所以,它的表面积和原来比没有变化.
故答案为:没有变化.
【点评】此题考查的目的是理解掌握正方体表面积的意义及应用.
11.【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,正方体的表面积公式:S=6a2,体积公式:V=a3,把数据代入公式解答。
【解答】解:(0.8×0.5+0.8×0.4+0.5×0.4)×2
=(0.4+0.32+0.2)×2
=0.92×2
=1.84(平方米)
0.8×0.5×0.4
=0.4×0.4
=0.16(立方米)
(12×9+12×6+9×6)×2
=(108+72+54)×2
=234×2
=468(平方厘米)
12×9×6
=108×6
=648(立方厘米)
7×7×6
=49×6
=294(平方分米)
7×7×7
=49×7
=343(立方分米)
填表如下:
长 宽 高 表面积 体积
长方体 0.8m 0.5m 0.4m 1.84m2 0.16m3
12cm 9cm 6cm 468cm2 648cm3
正方体 棱长7dm 294dm2 343dm3
故答案为:1.84平方米,0.16立方米;468平方厘米,648立方厘米;294平方分米,343立方分米。
【点评】此题主要考查长方体、正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
三.应用题(共5小题)
12.【分析】根据长方体的特征:12条棱分为互相平行的3组,每组4条棱的长度相等,由图形可知:所需彩带的长度等于4条高、2条长、2条宽棱的长度和再加上接头处用的22厘米即可。
【解答】解:(20+20)×2+10×4+22
=40×2+40+22
=80+40+22
=142(厘米)
答:需要142厘米长的彩带。
【点评】此题考查的目的是掌握长方体的棱的特征,根据棱长总和的计算方法解答。
13.【分析】根据题意可知,把这个长方体木块削成一个最大的正方体,削成的正方体的棱长等于长方体的高,根据正方体的表面积公式:S=6a2,把数据代入公式解答。
【解答】解:5×5×6
=25×6
=150(平方厘米)
答:涂油漆的面积是150平方厘米。
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式。
14.【分析】由于游泳池无盖,所以抹水泥部分的面积等于这个长方体的一个底面和4个侧面的总面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出抹水泥的面积,然后根据单价×数量=总价,求出一共需要多少元。
【解答】解:8×6+8×2×2+6×2×2
=48+32+24
=104(平方米)
12×104=1248(元)
答:抹水泥的面积是104平方米,这些水泥一共1248元。
【点评】此题主要考查长方体表面积公式的灵活运用,关键 是熟记公式。
15.【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,由于地面不需要粉刷,所以求出这个长方体的一个底面和4个侧面的总面积,再减去门窗面积就是粉刷的面积,然后用粉刷的面积乘每平方米用涂料的质量即可。
【解答】解:9×6+9×3×2+6×3×2﹣21.7
=54+54+36﹣21.7
=144﹣21.7
=122.3(平方米)
122.3×0.5=61.15(千克)
答:要粉刷的面积是122.3平方米,一共要用涂料61.15千克。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
16.【分析】通过观察图形可知,做这个盒子用铁皮的面积等于原来长方形铁皮的面积减去4个边长是4厘米的正方形的面积,根据长方形的面积公式:S=ab,正方形的面积公式:S=a2,把数据代入公式求出它们的面积差即可。
【解答】解:28×24﹣4×4×4
=672﹣16×4
=672﹣64
=608(平方厘米)
答:这个盒子用了608平方厘米铁皮。
【点评】此题考查目的是理解掌握长方体表面积的意义,以及长方形、正方形面积公式的灵活运用,关键是熟记公式。
第1页(共3页)
一.选择题(共6小题)
1.如图,甲的表面积比乙的表面积( )
A.大 B.小 C.相等 D.无法确定
2.将四个长10cm,宽8cm,高3cm的长方体盒子,用彩纸包在一起,最省包装纸的方法是( )
A. B. C. D.
3.如果把一个长10cm、宽5cm、高5cm的长方体,切成两个完全一样的正方体,切成的两个正方体的表面积之和与原来长方体的表面积相比,( )
A.变大了 B.变小了 C.不变
4.把三个棱长是3cm的小正方体拼成一个长方体,长方体的表面积比三个小正方体的表面积之和少( )cm2。
A.27 B.54 C.36
5.一个长方体照如图沿虚线切三刀,切成若干个小长方体,这些小长方体的表面积之和比原来大长方体的表面积增加了90平方厘米。原来长方体的表面积是( )平方厘米。
A.30 B.90 C.180 D.270
6.如图是用棱长为2厘米的正方体摆成的物体,这个物体的表面积是( )平方厘米。
A.10 B.30 C.34 D.136
二.填空题(共5小题)
7.如图,一个长方体是由三个同样的正方体拼成的,如果去掉上面一个正方体,表面积就比原来减少32平方厘米。原来长方体的表面积是 平方厘米。
8.在一个长方体中相交于同一顶点的三条棱的长度之和是8.7分米,则这个长方体的棱长总和为 分米。
9.一根长3m的长方体木料,横截面是边长为6cm的正方形,把它平均锯成5段,表面积比原来增加了 cm2。
10.用8个同样大小的小正方体方块拼成一个大正方体,如果拿走其中1个小正方体方块,它的表面积和原来比 .(填“变大”“变小”或“没有变化”)
11.完成下表。
长 宽 高 表面积 体积
长方体 0.8m 0.5m 0.4m
12cm 9cm 6cm
正方体 棱长7dm
三.应用题(共5小题)
12.一种长方体的礼品盒(如图),用彩带捆扎起来(接头处共22cm),至少需要多少厘米的彩带?
13.把一个长8厘米,宽7厘米,高5厘米的长方体木块削切成一个最大的正方体,给这个正方体的表面涂上油漆,求涂油漆的面积是多少平方厘米?
14.有一个水池长8米,宽6米,高2米。现在要给它的底面及四周抹上水泥,抹水泥的面积是多少平方米?如果每平方米的水泥需12元,这些水泥一共要多少钱?
15.要粉刷教室的四壁及屋顶,教室长9米,宽6米,高3米,门窗的面积一共是21.7平方米,要粉刷的面积是多少平方米?如果每平方米用涂料0.5千克,一共要用涂料多少千克?
16.一块长28cm,宽24cm的长方形铁皮(如图),从四个角各切掉一个边长为4cm的正方形,然后做成盒子.这个盒子用了多少铁皮?
(同步作业-2.(长方体)-2021-2022学年下学期小学数学北师大版五年级
参考答案与试题解析
一.选择题(共6小题)
1.【分析】通过观察图形可知,乙图原来长方体顶点上的这个小正方体外露3个面,从顶点上挖掉1个小正方体后,又外露与原来相同的3个面,虽然体积减少了,但表面积不变。据此解答。
【解答】解:乙图原来长方体顶点上的这个小正方体外露3个面,从顶点上挖掉1个小正方体后,又外露与原来相同的3个面,虽然体积减少了,但表面积不变。
所以甲的表面积和乙的表面积相等。
故选:C。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用。
2.【分析】要想更省包装纸,需使表面积最小,由题意可知:只要求出哪种情况下,拼组后的大长方体的表面积与原来四个长方体的表面积之和相比,减少的面的面积最大,就最省包装纸。据此解答即可。
【解答】解:A、表面积减少了:(10×3+8×3)×4=54×4=216(平方厘米)
B、表面积减少了:10×8×6=80×6=480(平方厘米)
C、表面积减少了:(10×8+8×3)×4=104×4=416(平方厘米)
D、表面积减少了:(10×8+10×3)×4=110×4=440(平方厘米)
480>440>416>216
答:最省包装纸的方法是选项B。
故选:B。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用,关键是明确:要使拼组后的表面积最小,则把最大的面相粘合。
3.【分析】根据题意可知,把这个长方体切成两个完全一样的正方体,切成的两个正方体的表面积之和与原来长方体的表面积增加了两个切面的面积。据此解答。
【解答】解:如果把一个长10cm、宽5cm、高5cm的长方体,切成两个完全一样的正方体,切成的两个正方体的表面积之和与原来长方体的表面积相比变大了。
故选:A。
【点评】此题考查的目的是理解掌握长方体、正方体表面积的意义及应用。
4.【分析】根据题意可知,把三个棱长是3cm的小正方体拼成一个长方体,长方体的表面积比三个小正方体的表面积之和减少了正方体的4个面的面积,根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:3×3×4
=9×4
=36(平方厘米)
答:长方体的表面积比三个小正方体的表面积之和少36平方厘米。
故选:C。
【点评】此题考查的目的是理解掌握正方体、长方体表面积的意义,正方形面积公式的灵活运用,关键是熟记公式。
5.【分析】通过观察图形可知,与长方体的前后面平行切一刀增加的面积与前后面相同,同理:与上下面平行切一刀增加的面积与上下面相同;与左右面平行切一刀增加的面积与左右面相同,所以把这个长方体照如图沿虚线切三刀,这些小长方体的表面积之和比原来大长方体的表面积增加的面积就等于原来大长方体的表面积。据此解答即可。
【解答】解:与长方体的前后面平行切一刀增加的面积与前后面相同,同理:与上下面平行切一刀增加的面积与上下面相同;与左右面平行切一刀增加的面积与左右面相同,所以把这个长方体照如图沿虚线切三刀,这些小长方体的表面积之和比原来大长方体的表面积增加的面积就等于原来大长方体的表面积。
答:原来长方体的表面积是90平方厘米。
故选:B。
【点评】此题考查的目的是理解掌握长方体的特征,长方体表面积的意义及应用。
6.【分析】通过观察图形可知,前、后面都是正方体的5个面,上、下面都是正方体的7个面,左、右面都是正方体的5个面,根据正方形的面积公式:S=a2,求出正方体的一个面的面积,然后再乘这个组合图形外露的正方体的面的个数即可。
【解答】解:2×2×(5+7+5)×2
=4×17×2
=68×2
=136(平方厘米)
答:这个物体的表面积 136平方厘米。
故选:D。
【点评】此题主要考查正方体、长方体表面积公式的灵活运用,关键是弄清拼成组合图形的前后、上下、左右各外露多少个正方形的面。
二.填空题(共5小题)
7.【分析】根据题意可知,如果去掉上面一个正方体,表面积就比原来减少32平方厘米。表面积减少的是正方体的4个面的面积,据此可以求出正方体的一个面的面积,原来长方体的表面积等于正方体的14个面的面积。据此解答。
【解答】解:32÷4×14
=8×14
=112(平方厘米)
答:原来长方体的表面积是112平方厘米。
故答案为:112。
【点评】此题主要考查长方体、正方体表面积的意义及应用,关键是求出正方体的一个面的面积。
8.【分析】根据长方体的长、宽、高的意义,在长方体中相交于同一顶点的三条棱的长度分别叫做长方体的长、宽、高。在一个长方体中相交于同一顶点的三条棱的长度之和是8.7分米,也就是这个长方体的长、宽、高的和是8.7分米。再根据长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答。
【解答】解:8.7×4=34.8(分米)
答:这个长方体的棱长总和是34.8分米。
故答案为:34.8。
【点评】此题考查的目的是理解掌握长方体的特征,长方体棱长总和公式及应用。
9.【分析】根据题意可知,把这根木料平均锯成5段,需要锯4次,每锯一次就增加两个截面的面积,那么锯4次就增加8个截面的面积,根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:6×6×8
=36×8
=288(平方厘米)
答:表面积增加288平方厘米。
故答案为:288。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
10.【分析】因为在顶点处的小正方体外露3个面,拿掉一个小正方体后又外露与原来相同的3个面,所以表面积和原来相同.据此解答.
【解答】解:用8个同样大小的小正方体方块拼成一个大正方体,每个小正方体都在顶点上,因为在顶点处的小正方体外露3个面,拿掉一个小正方体后又外露与原来相同的3个面,所以表面积和原来相同.
所以,它的表面积和原来比没有变化.
故答案为:没有变化.
【点评】此题考查的目的是理解掌握正方体表面积的意义及应用.
11.【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,正方体的表面积公式:S=6a2,体积公式:V=a3,把数据代入公式解答。
【解答】解:(0.8×0.5+0.8×0.4+0.5×0.4)×2
=(0.4+0.32+0.2)×2
=0.92×2
=1.84(平方米)
0.8×0.5×0.4
=0.4×0.4
=0.16(立方米)
(12×9+12×6+9×6)×2
=(108+72+54)×2
=234×2
=468(平方厘米)
12×9×6
=108×6
=648(立方厘米)
7×7×6
=49×6
=294(平方分米)
7×7×7
=49×7
=343(立方分米)
填表如下:
长 宽 高 表面积 体积
长方体 0.8m 0.5m 0.4m 1.84m2 0.16m3
12cm 9cm 6cm 468cm2 648cm3
正方体 棱长7dm 294dm2 343dm3
故答案为:1.84平方米,0.16立方米;468平方厘米,648立方厘米;294平方分米,343立方分米。
【点评】此题主要考查长方体、正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
三.应用题(共5小题)
12.【分析】根据长方体的特征:12条棱分为互相平行的3组,每组4条棱的长度相等,由图形可知:所需彩带的长度等于4条高、2条长、2条宽棱的长度和再加上接头处用的22厘米即可。
【解答】解:(20+20)×2+10×4+22
=40×2+40+22
=80+40+22
=142(厘米)
答:需要142厘米长的彩带。
【点评】此题考查的目的是掌握长方体的棱的特征,根据棱长总和的计算方法解答。
13.【分析】根据题意可知,把这个长方体木块削成一个最大的正方体,削成的正方体的棱长等于长方体的高,根据正方体的表面积公式:S=6a2,把数据代入公式解答。
【解答】解:5×5×6
=25×6
=150(平方厘米)
答:涂油漆的面积是150平方厘米。
【点评】此题主要考查正方体表面积公式的灵活运用,关键是熟记公式。
14.【分析】由于游泳池无盖,所以抹水泥部分的面积等于这个长方体的一个底面和4个侧面的总面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出抹水泥的面积,然后根据单价×数量=总价,求出一共需要多少元。
【解答】解:8×6+8×2×2+6×2×2
=48+32+24
=104(平方米)
12×104=1248(元)
答:抹水泥的面积是104平方米,这些水泥一共1248元。
【点评】此题主要考查长方体表面积公式的灵活运用,关键 是熟记公式。
15.【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,由于地面不需要粉刷,所以求出这个长方体的一个底面和4个侧面的总面积,再减去门窗面积就是粉刷的面积,然后用粉刷的面积乘每平方米用涂料的质量即可。
【解答】解:9×6+9×3×2+6×3×2﹣21.7
=54+54+36﹣21.7
=144﹣21.7
=122.3(平方米)
122.3×0.5=61.15(千克)
答:要粉刷的面积是122.3平方米,一共要用涂料61.15千克。
【点评】此题主要考查长方体表面积公式的灵活运用,关键是熟记公式。
16.【分析】通过观察图形可知,做这个盒子用铁皮的面积等于原来长方形铁皮的面积减去4个边长是4厘米的正方形的面积,根据长方形的面积公式:S=ab,正方形的面积公式:S=a2,把数据代入公式求出它们的面积差即可。
【解答】解:28×24﹣4×4×4
=672﹣16×4
=672﹣64
=608(平方厘米)
答:这个盒子用了608平方厘米铁皮。
【点评】此题考查目的是理解掌握长方体表面积的意义,以及长方形、正方形面积公式的灵活运用,关键是熟记公式。
第1页(共3页)
