1.2 磁场对运动电荷的作用力 同步训练(word版含答案)
文档属性
| 名称 | 1.2 磁场对运动电荷的作用力 同步训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 444.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-02 20:19:37 | ||
图片预览



文档简介
1.2 磁场对运动电荷的作用力 同步训练 2021—2022学年高中物理人教版(2019)选择性必修第二册
一、单选题
1.如图所示为洛伦兹力演示仪,当电子枪水平向左发射电子,电子在洛伦兹力作用下做圆周运动。则可判断两励磁线圈中电流方向(从读者目前的视角观察)( )
A.均为顺时针方向
B.均为逆时针方向
C.靠近观察者的线圈中电流为顺时针方向、另一线圈电流为逆时针方向
D.靠近观察者的线圈中电流为逆时针方向、另一线圈电流为顺时针方向
2.如图所示,在正方体的四条沿x轴方向的棱上,分别固定四根通有等大电流I0的等长导线。正方体的中心点P处有不断沿y轴正方向喷射粒子的粒子源,关于粒子刚被喷出时所受到的洛伦兹力方向,下列说法中正确的是 ( )
A.若粒子带正电,其所受的洛伦兹力方向沿z轴正方向
B.若粒子带正电,其所受的洛伦兹力方向沿x轴正方向
C.若粒子带负电,其所受的洛伦兹力方向沿x轴正方向
D.若粒子带负电,其所受的洛伦兹力方向沿z轴负方向
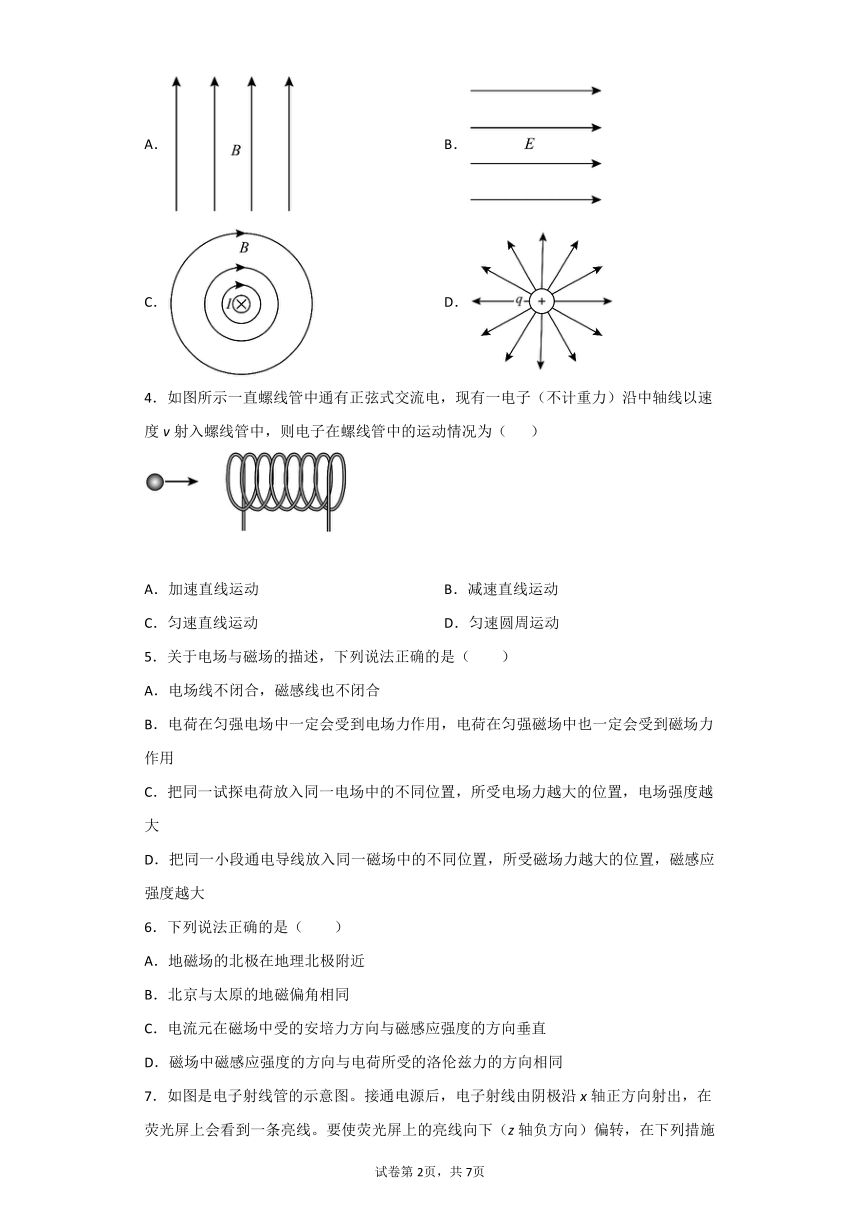
3.仅受洛伦兹力或电场力的作用,带正电的点电荷在下列磁场或电场中能做匀速圆周运动的是( )
A. B.
C. D.
4.如图所示一直螺线管中通有正弦式交流电,现有一电子(不计重力)沿中轴线以速度v射入螺线管中,则电子在螺线管中的运动情况为( )
A.加速直线运动 B.减速直线运动
C.匀速直线运动 D.匀速圆周运动
5.关于电场与磁场的描述,下列说法正确的是( )
A.电场线不闭合,磁感线也不闭合
B.电荷在匀强电场中一定会受到电场力作用,电荷在匀强磁场中也一定会受到磁场力作用
C.把同一试探电荷放入同一电场中的不同位置,所受电场力越大的位置,电场强度越大
D.把同一小段通电导线放入同一磁场中的不同位置,所受磁场力越大的位置,磁感应强度越大
6.下列说法正确的是( )
A.地磁场的北极在地理北极附近
B.北京与太原的地磁偏角相同
C.电流元在磁场中受的安培力方向与磁感应强度的方向垂直
D.磁场中磁感应强度的方向与电荷所受的洛伦兹力的方向相同
7.如图是电子射线管的示意图。接通电源后,电子射线由阴极沿x轴正方向射出,在荧光屏上会看到一条亮线。要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
A.加一电场,电场方向沿y轴正方向
B.加一电场,电场方向沿z轴负方向
C.加一磁场,磁场方向沿y轴正方向
D.加一磁场,磁场方向沿z轴负方向
8.下列说法正确的是( )
A.带电粒子在磁场中仅受洛伦兹力时速度可能变大
B.观看3D电影的眼镜用到了光的偏振
C.机械波的周期由介质决定
D.匀速圆周运动的动量不变
二、多选题
9.如图所示,平行放置的长直导线分别通以等大反向的电流I。某带正电粒子以一定速度从两导线的正中间射入,第一次如图甲所示两平行通电导线方向,第二次如图乙所示两垂直通电导线方向。不计粒子重力,下列说法正确的是( )
A.甲图虚线上的磁感应强度方向垂直纸面向里
B.乙图虚线上的粒子的速度方向与磁场垂直
C.甲图粒子将向上偏转,且速度大小保持不变
D.乙图粒子做直线运动,且速度先增大后减小
10.关于电场和磁场,下面说法正确的是( )
A.电场和磁场都是客观存在的物质
B.电场中,磁场中,电路中,都是比值定义式
C.点电荷形成的电场中,离点电荷越近电场强度一定越大
D.根据,电荷在磁场中运动时一定受到洛伦兹力
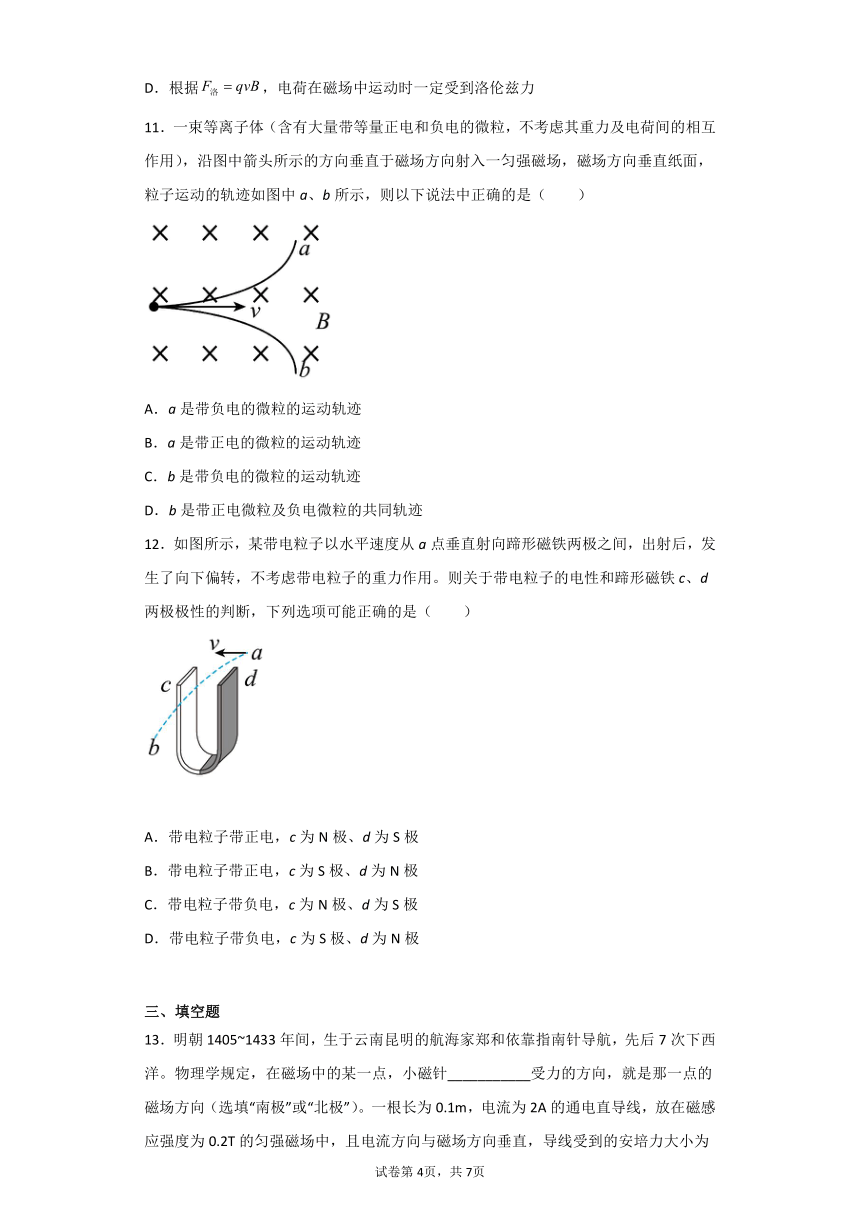
11.一束等离子体(含有大量带等量正电和负电的微粒,不考虑其重力及电荷间的相互作用),沿图中箭头所示的方向垂直于磁场方向射入一匀强磁场,磁场方向垂直纸面,粒子运动的轨迹如图中a、b所示,则以下说法中正确的是( )
A.a是带负电的微粒的运动轨迹
B.a是带正电的微粒的运动轨迹
C.b是带负电的微粒的运动轨迹
D.b是带正电微粒及负电微粒的共同轨迹
12.如图所示,某带电粒子以水平速度从a点垂直射向蹄形磁铁两极之间,出射后,发生了向下偏转,不考虑带电粒子的重力作用。则关于带电粒子的电性和蹄形磁铁c、d两极极性的判断,下列选项可能正确的是( )
A.带电粒子带正电,c为N极、d为S极
B.带电粒子带正电,c为S极、d为N极
C.带电粒子带负电,c为N极、d为S极
D.带电粒子带负电,c为S极、d为N极
三、填空题
13.明朝1405~1433年间,生于云南昆明的航海家郑和依靠指南针导航,先后7次下西洋。物理学规定,在磁场中的某一点,小磁针___________受力的方向,就是那一点的磁场方向(选填“南极”或“北极”)。一根长为0.1m,电流为2A的通电直导线,放在磁感应强度为0.2T的匀强磁场中,且电流方向与磁场方向垂直,导线受到的安培力大小为___________N;磁场对___________(选填“静止”或“运动”)电荷的作用力叫洛伦兹力。
14.导体棒中带电粒子的定向移动形成电流,电流可以从宏观和微观两个角度来认识,安培力与洛伦兹力也有宏观与微观的对应关系。
如图所示,静止不动的匀强磁场的磁感应强度大小为B,方向竖直向下。一段直导体棒长为L,横截面积为S,单位体积的自由电荷个数为n,自由电荷的电荷量为。导体棒中通有恒定电流,自由电荷的定向移动速率为(本题中两问均认为始终不变)。导体棒水平放置处于磁场中(垂直于磁感应强度)。
(1)若导体棒相对磁场静止,电荷定向运动时所受洛伦兹力的矢量和,在宏观上表现为导体棒所受的安培力。按照这个思路,请你由安培力的表达式推导出洛伦兹力大小的表达式。(______)
(2)概念学习中,类比与比较是常用的学习方法。我们已经知道,垂直于匀强磁场磁感线的通电导线所受的安培力,由此,我们用来定义磁感应强度。同样,运动方向垂直于匀强磁场磁感线的带电粒子所受的洛伦兹力,由此也可用洛伦兹力来定义磁感应强度,定义式是_________,把该定义式与电场强度的定义式进行对比,两个定义式(而非物理量)的差别在于:__________________
四、解答题
15.如图所示,两根倾斜直金属导轨、平行放置,它们所构成的轨道平面与水平面之间的夹角,两轨道之间的距离。一根质量的均匀直金属杆放在两导轨上,并与导轨垂直,且接触良好,整套装置处于与杆垂直的匀强磁场中。在导轨的上端接有电动势、内阻的直流电源和电阻箱R。当电阻箱接入电路中的电阻时,金属杆静止在轨道上。已知导轨与金属杆的电阻均可忽略不计,忽略一切摩擦阻力,,重力加速度。
(1)如果磁场方向竖直向下,求满足条件的磁感应强度的大小;
(2)如果磁场的方向可以随意调整,求满足条件的磁感应强度的最小值及方向。
(3)磁场与电场有诸多相似之处。电场强度的定义式,请你由此类比,从运动电荷所受的洛仑兹力出发,写出磁感应强度B的定义式。垂直于匀强磁场磁感线的通电导线所受的安培力。我们也可以用来定义磁感应强度,请从宏观与微观统一的思想出发构建一个合适的模型,推理论证该定义式与上述从洛仑兹力出发给出的磁感应强度B的定义式的一致性。
16.一质量为、带负电的电量为的小物体,由静止沿倾角为θ的光滑绝缘斜面开始下滑,整个装置在一个足够大的匀强磁场中,磁场方向垂直于纸面向里,磁感应强度为,如图所示。当物体滑到某一位置开始离开斜面,求:
(1)物体离开斜面时的速度;
(2)物体在斜面上滑行的距离。
17.导线中自由电子的定向移动形成电流,电流可以从宏观和微观两个角度来认识。
(1)一段通电直导线的横截面积为S,单位体积内自由电子个数为n,自由电子定向运动的速率为v,电子的电荷量为e。
①根据电流的定义式,推导该导线中电流的表达式;
②如图所示,电荷定向运动时所受洛伦兹力的矢量和,宏观上表现为导线所受的安培力。按照这个思路,请你尝试由安培力的表达式推导出洛伦兹力的表达式。
(2)经典物理学认为金属导体中恒定电场形成稳恒电流。金属导体中的自由电子在电场力的作用下,做定向运动,在此过程中,不断与金属离子发生碰撞。通过电场力和碰撞“阻力”做功,将电场能转化为内能,使金属离子的热运动更加剧烈,这就是焦耳热产生的原因。设金属导体长为L,横截面积为S,两端电压为U,电阻为R,通过的电流为I。请从大量自由电荷在电场力作用下,宏观上表现为匀速运动的做功和能量的转化守恒的角度,推导:在时间t内导线中产生的焦耳热可表达为Q=I2Rt(所需的其他中间量,可以自己设令)
18.关于洛伦兹力,下面三名同学有着不同的看法。
同学甲:运动电荷在磁感应强度不为零的地方,一定受到洛伦兹力的作用;而运动电荷在某处不受洛伦兹力作用,则该处的磁感应强度一定为零。
同学乙:洛伦兹力对带电粒子不做功,因此既不能改变带电粒子的动能,也不能改变带电粒子的速度。
同学丙:一个电子穿过某一空间未发生偏转,此空间可能有相互正交的匀强磁场和匀强电场。
他们的看法是否正确?为什么?
试卷第1页,共3页
试卷第2页,共2页
参考答案
1.A
2.C
3.A
4.C
5.C
6.C
7.C
8.B
9.AC
10.AC
11.BC
12.AD
13.北极 0.04 运动
14. 磁感应强度是描述磁场力的性质的物理量,它的方向是小磁针静止时N极的受力方向;电场强度是描述电场力的性质的物理量,它的方向与正电荷的受力方向相同
15.(1)0.3T;(2)0.24T,方向垂直于轨道平面斜向下;(3)由洛伦兹力公式得
F洛=qvB
可知
根据题意构建模型如下:
如图所示,在一匀强磁场中有一段固定的长为L的直导线,已知导线横截面积为S,单位体积内自由电荷数为n,导线内自由电荷定向运动速率为v,磁场的磁感应强度为B
则导线内自由电荷数
N=nSL
安培力与洛伦兹力的关系为
F安=N F洛
导线内电流的微观表达式
I=nqSv
联立上面三个式子可得
即定义式与这一定义式是一致的.
16.(1);(2)
17.(1)①.在时间t内流过导线横截面的电子数
N=nvSt
通过导线横截面的总电荷量
Q=Ne
导线中电流
联立以上三式可得
I=nvSe
②.导线受安培力的大小F安=BIL,长L的导线内的总的带电粒子数
N=nSL
又
I=nvSe
电荷定向运动时所受洛伦兹力的矢量和,表现为导线所受的安培力,即
Nf=F安
联立以上三式可以推导出洛伦兹力的表达式
f=evB
(2)设金属导体长为L,横截面积为S,两端电压为U,导线中的电场强度
金属导体中单位体积中的自由电子数为n,则金属导体中自由电子数
N=nSL
自由电子的带电量为e,连续两次碰撞时间间隔 t,定向移动的速度为v,则一次碰撞的能量转移
eEv t=mv′2-0
一个自由电子在时间t内与金属离子碰撞次数为;金属导体中在时间t内全部自由电子与金属离子碰撞,产生的焦耳热
又
I=neSv
U=IR
联立解以上各式推导可得
Q=I2Rt
18.甲同学:根据洛伦力公式知,运动电荷是否受洛伦兹力不仅与B有关,还和θ有关。如果B和θ有一个为零,则f一定为零,但如果f为零,则不一定是B为零。故甲说法错误;
乙同学:因为洛伦兹力始终与速度垂直,所以洛伦兹力对带电粒子不做功,不会改变动能。粒子只受洛伦兹力时,根据物体做曲线运动的条件知,粒子一定做曲线运动,速度的方向发生改变,速度是矢量,所以速度会改变。故乙同学说法错误。
丙同学:一个电子穿过某一空间未发生偏转,可能粒子受合力为零,也可能不受力,也可能受力与速度在同一直线上,如果有相互正交的匀强磁场和匀强电场,电子受合力有可能为零,电子将做匀速直线运动,故丙同学说法正确。
一、单选题
1.如图所示为洛伦兹力演示仪,当电子枪水平向左发射电子,电子在洛伦兹力作用下做圆周运动。则可判断两励磁线圈中电流方向(从读者目前的视角观察)( )
A.均为顺时针方向
B.均为逆时针方向
C.靠近观察者的线圈中电流为顺时针方向、另一线圈电流为逆时针方向
D.靠近观察者的线圈中电流为逆时针方向、另一线圈电流为顺时针方向
2.如图所示,在正方体的四条沿x轴方向的棱上,分别固定四根通有等大电流I0的等长导线。正方体的中心点P处有不断沿y轴正方向喷射粒子的粒子源,关于粒子刚被喷出时所受到的洛伦兹力方向,下列说法中正确的是 ( )
A.若粒子带正电,其所受的洛伦兹力方向沿z轴正方向
B.若粒子带正电,其所受的洛伦兹力方向沿x轴正方向
C.若粒子带负电,其所受的洛伦兹力方向沿x轴正方向
D.若粒子带负电,其所受的洛伦兹力方向沿z轴负方向
3.仅受洛伦兹力或电场力的作用,带正电的点电荷在下列磁场或电场中能做匀速圆周运动的是( )
A. B.
C. D.
4.如图所示一直螺线管中通有正弦式交流电,现有一电子(不计重力)沿中轴线以速度v射入螺线管中,则电子在螺线管中的运动情况为( )
A.加速直线运动 B.减速直线运动
C.匀速直线运动 D.匀速圆周运动
5.关于电场与磁场的描述,下列说法正确的是( )
A.电场线不闭合,磁感线也不闭合
B.电荷在匀强电场中一定会受到电场力作用,电荷在匀强磁场中也一定会受到磁场力作用
C.把同一试探电荷放入同一电场中的不同位置,所受电场力越大的位置,电场强度越大
D.把同一小段通电导线放入同一磁场中的不同位置,所受磁场力越大的位置,磁感应强度越大
6.下列说法正确的是( )
A.地磁场的北极在地理北极附近
B.北京与太原的地磁偏角相同
C.电流元在磁场中受的安培力方向与磁感应强度的方向垂直
D.磁场中磁感应强度的方向与电荷所受的洛伦兹力的方向相同
7.如图是电子射线管的示意图。接通电源后,电子射线由阴极沿x轴正方向射出,在荧光屏上会看到一条亮线。要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
A.加一电场,电场方向沿y轴正方向
B.加一电场,电场方向沿z轴负方向
C.加一磁场,磁场方向沿y轴正方向
D.加一磁场,磁场方向沿z轴负方向
8.下列说法正确的是( )
A.带电粒子在磁场中仅受洛伦兹力时速度可能变大
B.观看3D电影的眼镜用到了光的偏振
C.机械波的周期由介质决定
D.匀速圆周运动的动量不变
二、多选题
9.如图所示,平行放置的长直导线分别通以等大反向的电流I。某带正电粒子以一定速度从两导线的正中间射入,第一次如图甲所示两平行通电导线方向,第二次如图乙所示两垂直通电导线方向。不计粒子重力,下列说法正确的是( )
A.甲图虚线上的磁感应强度方向垂直纸面向里
B.乙图虚线上的粒子的速度方向与磁场垂直
C.甲图粒子将向上偏转,且速度大小保持不变
D.乙图粒子做直线运动,且速度先增大后减小
10.关于电场和磁场,下面说法正确的是( )
A.电场和磁场都是客观存在的物质
B.电场中,磁场中,电路中,都是比值定义式
C.点电荷形成的电场中,离点电荷越近电场强度一定越大
D.根据,电荷在磁场中运动时一定受到洛伦兹力
11.一束等离子体(含有大量带等量正电和负电的微粒,不考虑其重力及电荷间的相互作用),沿图中箭头所示的方向垂直于磁场方向射入一匀强磁场,磁场方向垂直纸面,粒子运动的轨迹如图中a、b所示,则以下说法中正确的是( )
A.a是带负电的微粒的运动轨迹
B.a是带正电的微粒的运动轨迹
C.b是带负电的微粒的运动轨迹
D.b是带正电微粒及负电微粒的共同轨迹
12.如图所示,某带电粒子以水平速度从a点垂直射向蹄形磁铁两极之间,出射后,发生了向下偏转,不考虑带电粒子的重力作用。则关于带电粒子的电性和蹄形磁铁c、d两极极性的判断,下列选项可能正确的是( )
A.带电粒子带正电,c为N极、d为S极
B.带电粒子带正电,c为S极、d为N极
C.带电粒子带负电,c为N极、d为S极
D.带电粒子带负电,c为S极、d为N极
三、填空题
13.明朝1405~1433年间,生于云南昆明的航海家郑和依靠指南针导航,先后7次下西洋。物理学规定,在磁场中的某一点,小磁针___________受力的方向,就是那一点的磁场方向(选填“南极”或“北极”)。一根长为0.1m,电流为2A的通电直导线,放在磁感应强度为0.2T的匀强磁场中,且电流方向与磁场方向垂直,导线受到的安培力大小为___________N;磁场对___________(选填“静止”或“运动”)电荷的作用力叫洛伦兹力。
14.导体棒中带电粒子的定向移动形成电流,电流可以从宏观和微观两个角度来认识,安培力与洛伦兹力也有宏观与微观的对应关系。
如图所示,静止不动的匀强磁场的磁感应强度大小为B,方向竖直向下。一段直导体棒长为L,横截面积为S,单位体积的自由电荷个数为n,自由电荷的电荷量为。导体棒中通有恒定电流,自由电荷的定向移动速率为(本题中两问均认为始终不变)。导体棒水平放置处于磁场中(垂直于磁感应强度)。
(1)若导体棒相对磁场静止,电荷定向运动时所受洛伦兹力的矢量和,在宏观上表现为导体棒所受的安培力。按照这个思路,请你由安培力的表达式推导出洛伦兹力大小的表达式。(______)
(2)概念学习中,类比与比较是常用的学习方法。我们已经知道,垂直于匀强磁场磁感线的通电导线所受的安培力,由此,我们用来定义磁感应强度。同样,运动方向垂直于匀强磁场磁感线的带电粒子所受的洛伦兹力,由此也可用洛伦兹力来定义磁感应强度,定义式是_________,把该定义式与电场强度的定义式进行对比,两个定义式(而非物理量)的差别在于:__________________
四、解答题
15.如图所示,两根倾斜直金属导轨、平行放置,它们所构成的轨道平面与水平面之间的夹角,两轨道之间的距离。一根质量的均匀直金属杆放在两导轨上,并与导轨垂直,且接触良好,整套装置处于与杆垂直的匀强磁场中。在导轨的上端接有电动势、内阻的直流电源和电阻箱R。当电阻箱接入电路中的电阻时,金属杆静止在轨道上。已知导轨与金属杆的电阻均可忽略不计,忽略一切摩擦阻力,,重力加速度。
(1)如果磁场方向竖直向下,求满足条件的磁感应强度的大小;
(2)如果磁场的方向可以随意调整,求满足条件的磁感应强度的最小值及方向。
(3)磁场与电场有诸多相似之处。电场强度的定义式,请你由此类比,从运动电荷所受的洛仑兹力出发,写出磁感应强度B的定义式。垂直于匀强磁场磁感线的通电导线所受的安培力。我们也可以用来定义磁感应强度,请从宏观与微观统一的思想出发构建一个合适的模型,推理论证该定义式与上述从洛仑兹力出发给出的磁感应强度B的定义式的一致性。
16.一质量为、带负电的电量为的小物体,由静止沿倾角为θ的光滑绝缘斜面开始下滑,整个装置在一个足够大的匀强磁场中,磁场方向垂直于纸面向里,磁感应强度为,如图所示。当物体滑到某一位置开始离开斜面,求:
(1)物体离开斜面时的速度;
(2)物体在斜面上滑行的距离。
17.导线中自由电子的定向移动形成电流,电流可以从宏观和微观两个角度来认识。
(1)一段通电直导线的横截面积为S,单位体积内自由电子个数为n,自由电子定向运动的速率为v,电子的电荷量为e。
①根据电流的定义式,推导该导线中电流的表达式;
②如图所示,电荷定向运动时所受洛伦兹力的矢量和,宏观上表现为导线所受的安培力。按照这个思路,请你尝试由安培力的表达式推导出洛伦兹力的表达式。
(2)经典物理学认为金属导体中恒定电场形成稳恒电流。金属导体中的自由电子在电场力的作用下,做定向运动,在此过程中,不断与金属离子发生碰撞。通过电场力和碰撞“阻力”做功,将电场能转化为内能,使金属离子的热运动更加剧烈,这就是焦耳热产生的原因。设金属导体长为L,横截面积为S,两端电压为U,电阻为R,通过的电流为I。请从大量自由电荷在电场力作用下,宏观上表现为匀速运动的做功和能量的转化守恒的角度,推导:在时间t内导线中产生的焦耳热可表达为Q=I2Rt(所需的其他中间量,可以自己设令)
18.关于洛伦兹力,下面三名同学有着不同的看法。
同学甲:运动电荷在磁感应强度不为零的地方,一定受到洛伦兹力的作用;而运动电荷在某处不受洛伦兹力作用,则该处的磁感应强度一定为零。
同学乙:洛伦兹力对带电粒子不做功,因此既不能改变带电粒子的动能,也不能改变带电粒子的速度。
同学丙:一个电子穿过某一空间未发生偏转,此空间可能有相互正交的匀强磁场和匀强电场。
他们的看法是否正确?为什么?
试卷第1页,共3页
试卷第2页,共2页
参考答案
1.A
2.C
3.A
4.C
5.C
6.C
7.C
8.B
9.AC
10.AC
11.BC
12.AD
13.北极 0.04 运动
14. 磁感应强度是描述磁场力的性质的物理量,它的方向是小磁针静止时N极的受力方向;电场强度是描述电场力的性质的物理量,它的方向与正电荷的受力方向相同
15.(1)0.3T;(2)0.24T,方向垂直于轨道平面斜向下;(3)由洛伦兹力公式得
F洛=qvB
可知
根据题意构建模型如下:
如图所示,在一匀强磁场中有一段固定的长为L的直导线,已知导线横截面积为S,单位体积内自由电荷数为n,导线内自由电荷定向运动速率为v,磁场的磁感应强度为B
则导线内自由电荷数
N=nSL
安培力与洛伦兹力的关系为
F安=N F洛
导线内电流的微观表达式
I=nqSv
联立上面三个式子可得
即定义式与这一定义式是一致的.
16.(1);(2)
17.(1)①.在时间t内流过导线横截面的电子数
N=nvSt
通过导线横截面的总电荷量
Q=Ne
导线中电流
联立以上三式可得
I=nvSe
②.导线受安培力的大小F安=BIL,长L的导线内的总的带电粒子数
N=nSL
又
I=nvSe
电荷定向运动时所受洛伦兹力的矢量和,表现为导线所受的安培力,即
Nf=F安
联立以上三式可以推导出洛伦兹力的表达式
f=evB
(2)设金属导体长为L,横截面积为S,两端电压为U,导线中的电场强度
金属导体中单位体积中的自由电子数为n,则金属导体中自由电子数
N=nSL
自由电子的带电量为e,连续两次碰撞时间间隔 t,定向移动的速度为v,则一次碰撞的能量转移
eEv t=mv′2-0
一个自由电子在时间t内与金属离子碰撞次数为;金属导体中在时间t内全部自由电子与金属离子碰撞,产生的焦耳热
又
I=neSv
U=IR
联立解以上各式推导可得
Q=I2Rt
18.甲同学:根据洛伦力公式知,运动电荷是否受洛伦兹力不仅与B有关,还和θ有关。如果B和θ有一个为零,则f一定为零,但如果f为零,则不一定是B为零。故甲说法错误;
乙同学:因为洛伦兹力始终与速度垂直,所以洛伦兹力对带电粒子不做功,不会改变动能。粒子只受洛伦兹力时,根据物体做曲线运动的条件知,粒子一定做曲线运动,速度的方向发生改变,速度是矢量,所以速度会改变。故乙同学说法错误。
丙同学:一个电子穿过某一空间未发生偏转,可能粒子受合力为零,也可能不受力,也可能受力与速度在同一直线上,如果有相互正交的匀强磁场和匀强电场,电子受合力有可能为零,电子将做匀速直线运动,故丙同学说法正确。
