广东省普宁市城东中学2013届高三第三次月考数学(理)试题
文档属性
| 名称 | 广东省普宁市城东中学2013届高三第三次月考数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 278.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-21 19:24:06 | ||
图片预览



文档简介
普宁市城东中学2012-2013学年度第一学期第三次月考
高三数学(理科)试卷
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在答题卷上)
1.设集合A={x|2x-2<1},B={x|y=ln(1-x)},则A∩B为( )
A.{x|x<2} B.{x|12.设p,q是两个命题:p:|x|-3>0,q:x2-x+>0,则p是q的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知g(x)=1-2x,f[g(x)]=(x≠0),则等于( )
A.1 B.2 C.3 D.15
4.函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,函数
g(x)=-x3+2x2+mx+5 在(-∞,+∞)内单调递减,则实数m等于( )
A.2 B.-2 C.±2 D.0
5.二次函数f(x)满足f(x+2)=f(2-x),且f(a)≤f(0)≤f(1),则实数a的取值范围是( )
A.a≥0 B.a≤0 C.0≤a≤4 D.a≤0或a≥4
6.函数的零点所在区间为( )
A. B. C. D.
7. 已知函数,则F(x)的极小值为( )
A.- B. C.- D.
8.在下列四个函数中,满足性质:“对于区间(1,2)上的任意
x1,x2(x1≠x2 ),恒成立”的只有( )
A.f(x)= B. C.f(x)=2x D.f(x)=x2
二、填空题:(本大题共7小题,考生作答6小题,每小题5分,满分30分.请将正确答案答在答题卷上)
(一)必做题(9~13题)
9.方程x2-2ax+4=0的两根均大于1,则实数a的范围是_______.
10. 已知a∈R,若关于x的方程x2+x+|a-|+|a|=0有实根,则a的取值范围是_______.
11. =________.
12. 在R上可导的函数f(x)的图象如右图所示,
则关于x的不等式x·f′(x)<0的解集为_______.
13.已知函数f(x)=2x-1,g(x)=1-x2,构造函数F(x)定义如下:当|f(x)|≥g(x)时,F(x)=|f(x)|;当|f(x)|(二)选做题(14~15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题) 在极坐标系中,圆C:ρ=6cos θ和
直线l:3ρcos θ-4ρsin θ-4=0相交于A,B两点,则线段AB的长
是________.
15.(几何证明选讲选做题)如图所示,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=,∠OAP=30°,则CP=____.
21世纪教育网
三、解答题. 本大题共6小题,满分80分. 解答须写出文字说明、证明过程或演算步骤.
16.(本题满分12分)已知函数
一个周期的图象如图所示,
(1)求函数的表达式;
(2)若,
且为的一个内角,求的值.
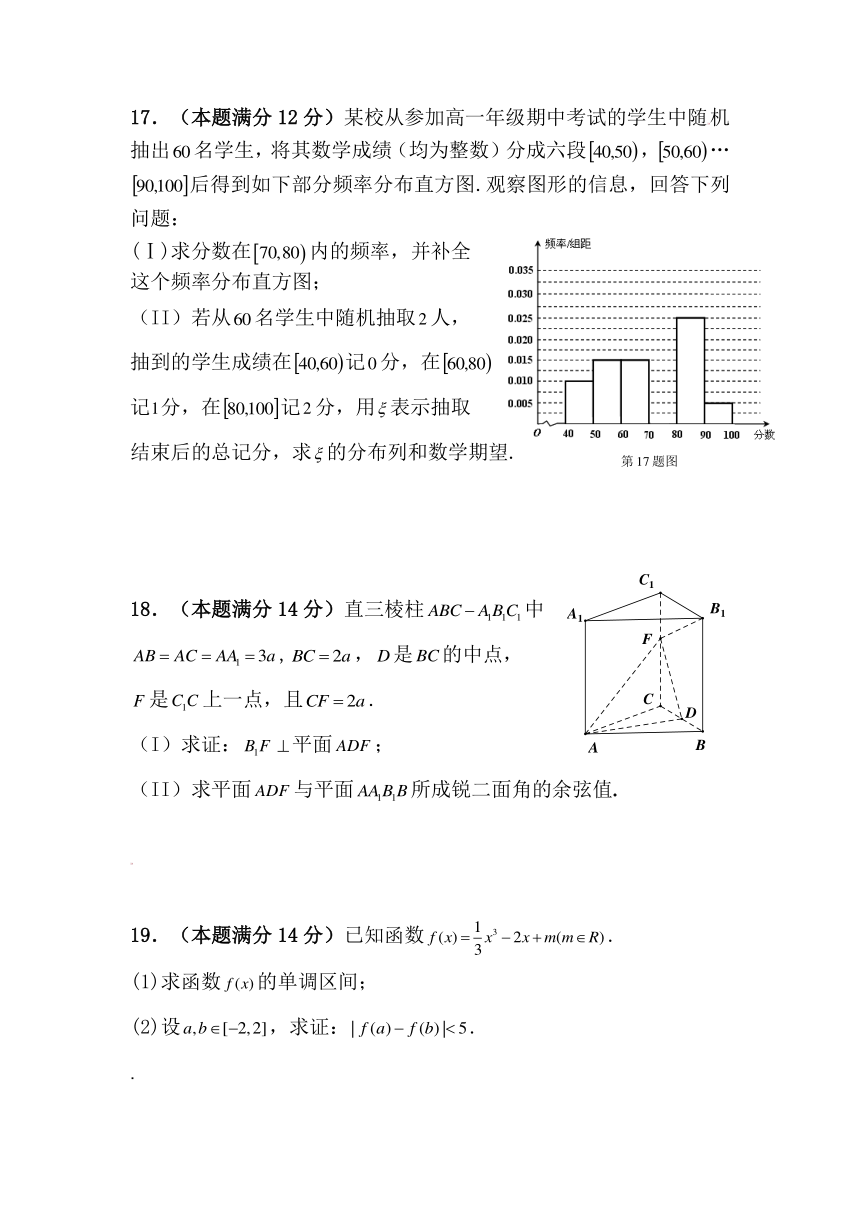
17.(本题满分12分)某校从参加高一年级期中考试的学生中随机抽出名学生,将其数学成绩(均为整数)分成六段,…后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在内的频率,并补全
这个频率分布直方图;
(II)若从名学生中随机抽取人,
抽到的学生成绩在记分,在
记分,在记分,用表示抽取
结束后的总记分,求的分布列和数学期望.
18.(本题满分14分)直三棱柱中
,,是的中点,
是上一点,且.
(I)求证:平面;
(II)求平面与平面所成锐二面角的余弦值.
19.(本题满分14分)已知函数.
(1)求函数的单调区间;
(2)设,求证:.
.
20.(本题满分14分)
设讨论函数
21.(本题满分14分)
设函数f(x)=x2+bln(x+1),其中b≠0.
(1)若b=-12,求f(x)在[1,3]的最小值;
(2)如果f(x)在定义域内既有极大值又有极小值,求实数b的取值范围;
(3)是否存在最小的正整数N,使得当n≥N时,不等式ln>恒成立.
普宁市城东中学2012-2013学年度第一学期第三次月考高三数学(理科)(答案)
一、选择题:CADBD CAA
二、填空题:
9、2≤a< 10、[0,] 11、 12、(-∞,-1)∪(0,1) 13、-1
14、 15、 a
三、解答题:
16.解:(1)从图知,函数的最大值为,则,函数的周期为, 而,则, 又时,,∴,而,则,∴函数的表达式为
(2)由得:,化简得:
,∴ ,由于,则,但,则,即A为锐角,从而,因此 .
17.解:(Ⅰ)设分数在内的频率为,根据频率分布直方图,则有
,
[来源:21世纪教育网]
可得,所以频率分布直方图如右图所示.
(Ⅱ)在的有人.并且的可能取值是.
则;; ;
;.
所以的分布列为
0
1
2
3
4
21世纪教育网
18.解法一:∵,是的中点,∴.又平面平面,
平面平面=,则平面.∴,在矩形中
,∴,,因此 ∴平面
解法二:以为坐标原点,、、分别为
、、轴建立空间直角坐标系(是的中点),易知
,,, ,
, ,,
由且,得, ,
即得平面;
解(II):由(1)知,,设平面的一个法向量为,则且,可取,
由 =-,即所求二面角的余弦值是.
19.解:(1)易得.当时,,单调递减;
当或时,,单调递增.
∴单调的单调递减区间为;单调的单调递增区间为.
(2)由(1)知函数在上的极大值为,极小值为
;又,;在上的最大值
,最小值为.
∴。
20.解:函数的定义域为
当的判别式
①当有两个零点,
且当内为增函数;
当内为减函数;
②当内为增函数;
③当内为增函数;
④当
在定义域内有唯一零点,
且当内为增函数;当时,
内为减函数。 的单调区间如下表:
(其中)
21.解:(1)由题意知,f(x)的定义域为(-1,+∞),b=-12时,由
f′(x)=2x-==0,得x=2(x=-3舍去),
当x∈[1,2)时,f′(x)<0,当x∈(2,3]时,f′(x)>0,
所以当x∈[1,2)时,f(x)单调递减;当x∈(2,3]时,f(x)单调递增,
所以f(x)min=f(2)=4-12ln 3.
(2)由题意f′(x)=2x+==0在(-1,+∞)有两个不等实根,即
2x2+2x+b=0在(-1,+∞)有两个不等实根,
设g(x)=2x2+2x+b,则,解之得0(3)当b=-1时,函数f=x2-ln(x+1),
令函数h=x3-f(x)=x3-x2+ln(x+1)
则h′=3x2-2x+=,
∴当x∈[0,+∞)时,h′>0.所以函数h在[0,+∞)上单调递增,又h(0)=0,∴x∈(0,+∞)时,恒有h>h(0)=0,
即x2则有恒成立.显然,存在最小的正整数N=1,
使得当n≥N时,不等式恒成立.
高三数学(理科)试卷
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在答题卷上)
1.设集合A={x|2x-2<1},B={x|y=ln(1-x)},则A∩B为( )
A.{x|x<2} B.{x|1
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知g(x)=1-2x,f[g(x)]=(x≠0),则等于( )
A.1 B.2 C.3 D.15
4.函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,函数
g(x)=-x3+2x2+mx+5 在(-∞,+∞)内单调递减,则实数m等于( )
A.2 B.-2 C.±2 D.0
5.二次函数f(x)满足f(x+2)=f(2-x),且f(a)≤f(0)≤f(1),则实数a的取值范围是( )
A.a≥0 B.a≤0 C.0≤a≤4 D.a≤0或a≥4
6.函数的零点所在区间为( )
A. B. C. D.
7. 已知函数,则F(x)的极小值为( )
A.- B. C.- D.
8.在下列四个函数中,满足性质:“对于区间(1,2)上的任意
x1,x2(x1≠x2 ),恒成立”的只有( )
A.f(x)= B. C.f(x)=2x D.f(x)=x2
二、填空题:(本大题共7小题,考生作答6小题,每小题5分,满分30分.请将正确答案答在答题卷上)
(一)必做题(9~13题)
9.方程x2-2ax+4=0的两根均大于1,则实数a的范围是_______.
10. 已知a∈R,若关于x的方程x2+x+|a-|+|a|=0有实根,则a的取值范围是_______.
11. =________.
12. 在R上可导的函数f(x)的图象如右图所示,
则关于x的不等式x·f′(x)<0的解集为_______.
13.已知函数f(x)=2x-1,g(x)=1-x2,构造函数F(x)定义如下:当|f(x)|≥g(x)时,F(x)=|f(x)|;当|f(x)|
14.(坐标系与参数方程选做题) 在极坐标系中,圆C:ρ=6cos θ和
直线l:3ρcos θ-4ρsin θ-4=0相交于A,B两点,则线段AB的长
是________.
15.(几何证明选讲选做题)如图所示,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=,∠OAP=30°,则CP=____.
21世纪教育网
三、解答题. 本大题共6小题,满分80分. 解答须写出文字说明、证明过程或演算步骤.
16.(本题满分12分)已知函数
一个周期的图象如图所示,
(1)求函数的表达式;
(2)若,
且为的一个内角,求的值.
17.(本题满分12分)某校从参加高一年级期中考试的学生中随机抽出名学生,将其数学成绩(均为整数)分成六段,…后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在内的频率,并补全
这个频率分布直方图;
(II)若从名学生中随机抽取人,
抽到的学生成绩在记分,在
记分,在记分,用表示抽取
结束后的总记分,求的分布列和数学期望.
18.(本题满分14分)直三棱柱中
,,是的中点,
是上一点,且.
(I)求证:平面;
(II)求平面与平面所成锐二面角的余弦值.
19.(本题满分14分)已知函数.
(1)求函数的单调区间;
(2)设,求证:.
.
20.(本题满分14分)
设讨论函数
21.(本题满分14分)
设函数f(x)=x2+bln(x+1),其中b≠0.
(1)若b=-12,求f(x)在[1,3]的最小值;
(2)如果f(x)在定义域内既有极大值又有极小值,求实数b的取值范围;
(3)是否存在最小的正整数N,使得当n≥N时,不等式ln>恒成立.
普宁市城东中学2012-2013学年度第一学期第三次月考高三数学(理科)(答案)
一、选择题:CADBD CAA
二、填空题:
9、2≤a< 10、[0,] 11、 12、(-∞,-1)∪(0,1) 13、-1
14、 15、 a
三、解答题:
16.解:(1)从图知,函数的最大值为,则,函数的周期为, 而,则, 又时,,∴,而,则,∴函数的表达式为
(2)由得:,化简得:
,∴ ,由于,则,但,则,即A为锐角,从而,因此 .
17.解:(Ⅰ)设分数在内的频率为,根据频率分布直方图,则有
,
[来源:21世纪教育网]
可得,所以频率分布直方图如右图所示.
(Ⅱ)在的有人.并且的可能取值是.
则;; ;
;.
所以的分布列为
0
1
2
3
4
21世纪教育网
18.解法一:∵,是的中点,∴.又平面平面,
平面平面=,则平面.∴,在矩形中
,∴,,因此 ∴平面
解法二:以为坐标原点,、、分别为
、、轴建立空间直角坐标系(是的中点),易知
,,, ,
, ,,
由且,得, ,
即得平面;
解(II):由(1)知,,设平面的一个法向量为,则且,可取,
由 =-,即所求二面角的余弦值是.
19.解:(1)易得.当时,,单调递减;
当或时,,单调递增.
∴单调的单调递减区间为;单调的单调递增区间为.
(2)由(1)知函数在上的极大值为,极小值为
;又,;在上的最大值
,最小值为.
∴。
20.解:函数的定义域为
当的判别式
①当有两个零点,
且当内为增函数;
当内为减函数;
②当内为增函数;
③当内为增函数;
④当
在定义域内有唯一零点,
且当内为增函数;当时,
内为减函数。 的单调区间如下表:
(其中)
21.解:(1)由题意知,f(x)的定义域为(-1,+∞),b=-12时,由
f′(x)=2x-==0,得x=2(x=-3舍去),
当x∈[1,2)时,f′(x)<0,当x∈(2,3]时,f′(x)>0,
所以当x∈[1,2)时,f(x)单调递减;当x∈(2,3]时,f(x)单调递增,
所以f(x)min=f(2)=4-12ln 3.
(2)由题意f′(x)=2x+==0在(-1,+∞)有两个不等实根,即
2x2+2x+b=0在(-1,+∞)有两个不等实根,
设g(x)=2x2+2x+b,则,解之得0
令函数h=x3-f(x)=x3-x2+ln(x+1)
则h′=3x2-2x+=,
∴当x∈[0,+∞)时,h′>0.所以函数h在[0,+∞)上单调递增,又h(0)=0,∴x∈(0,+∞)时,恒有h>h(0)=0,
即x2
使得当n≥N时,不等式恒成立.
同课章节目录
