2021—2022学年人教版数学七年级下册7.2.1用坐标表示地理位置靶向训练习题 (word版、含解析)
文档属性
| 名称 | 2021—2022学年人教版数学七年级下册7.2.1用坐标表示地理位置靶向训练习题 (word版、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 478.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 20:19:13 | ||
图片预览

文档简介
2021—2022人教版数学七年级下册
7.2.1用坐标表示地理位置靶向训练(含解析)
一、单选题
1.从车站向东走400米,再向北走500米到小红家;从车站向北走500米,向西走200米到小强家,则( )
A.小强家在小红家正东 B.小强家在小红家正西
C.小强家在小红家正南 D.小强家在小红家正北
2.A地在地球上的位置如图所示,则A地的位置是( )
A.东经130°,北纬50° B.东经130°,北纬60°
C.东经140°,北纬50° D.东经40°,北纬50°
3.下列数据中不能确定物体位置的是( )
A.某市政府位于北京路32号 B.小明住在某小区3号楼7号
C.太阳在我们的正上方 D.东经130°,北纬54°的城市
4.在平面直角坐标系中,点P( +1,-2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.若点P(x,y)的坐标满足xy=0(x≠y),则点P必在( )
A.原点上 B.x轴上
C.y轴上 D.x轴上或y轴上(除原点)
6.点 所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
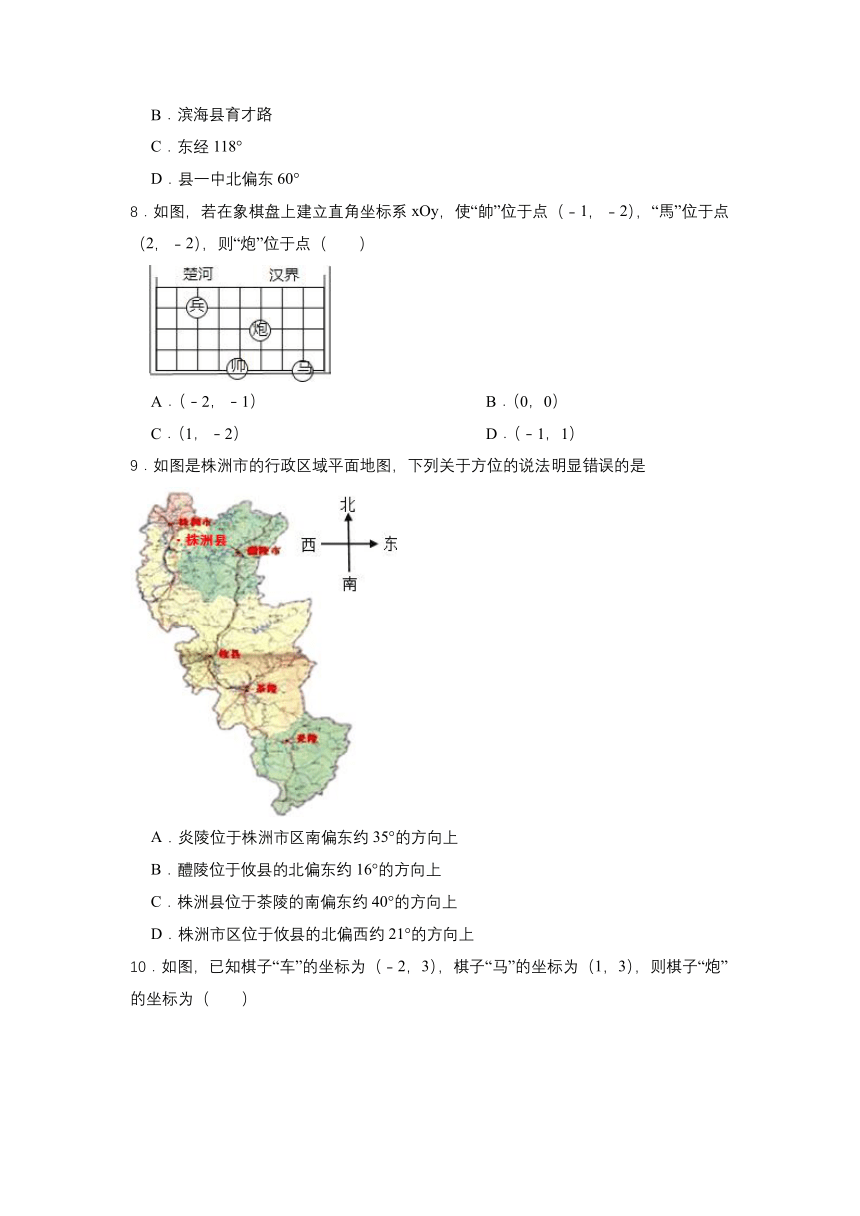
7.根据下列表述,能确定具体位置的是( )
A.我校八年级(1)班班级座位3排4列
B.滨海县育才路
C.东经118°
D.县一中北偏东60°
8.如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(﹣1,﹣2),“馬”位于点(2,﹣2),则“炮”位于点( )
A.(﹣2,﹣1) B.(0,0)
C.(1,﹣2) D.(﹣1,1)
9.如图是株洲市的行政区域平面地图,下列关于方位的说法明显错误的是
A.炎陵位于株洲市区南偏东约35°的方向上
B.醴陵位于攸县的北偏东约16°的方向上
C.株洲县位于茶陵的南偏东约40°的方向上
D.株洲市区位于攸县的北偏西约21°的方向上
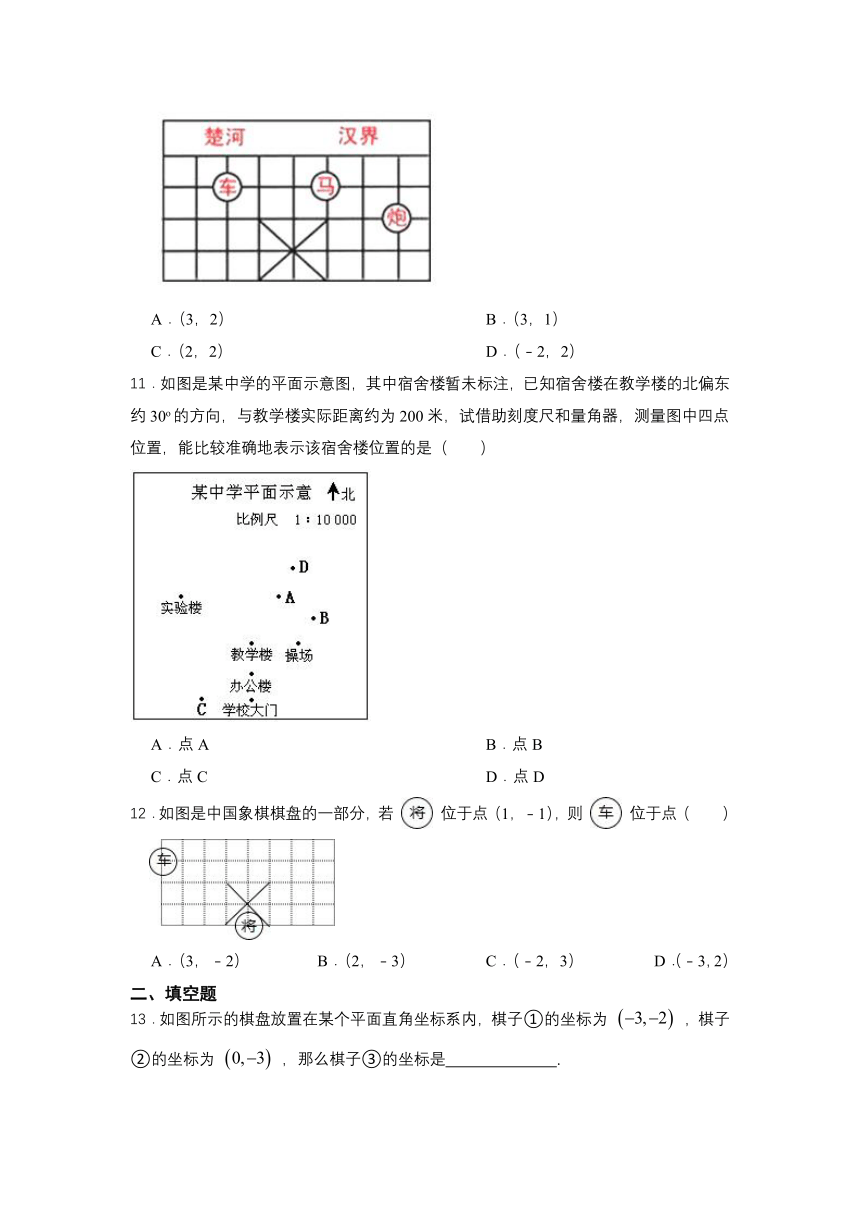
10.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(3,2) B.(3,1)
C.(2,2) D.(﹣2,2)
11.如图是某中学的平面示意图,其中宿舍楼暂未标注,已知宿舍楼在教学楼的北偏东约30o的方向,与教学楼实际距离约为200米,试借助刻度尺和量角器,测量图中四点位置,能比较准确地表示该宿舍楼位置的是( )
A.点A B.点B
C.点C D.点D
12.如图是中国象棋棋盘的一部分,若 位于点(1,﹣1),则 位于点( )
A.(3,﹣2) B.(2,﹣3) C.(﹣2,3) D.(﹣3,2)
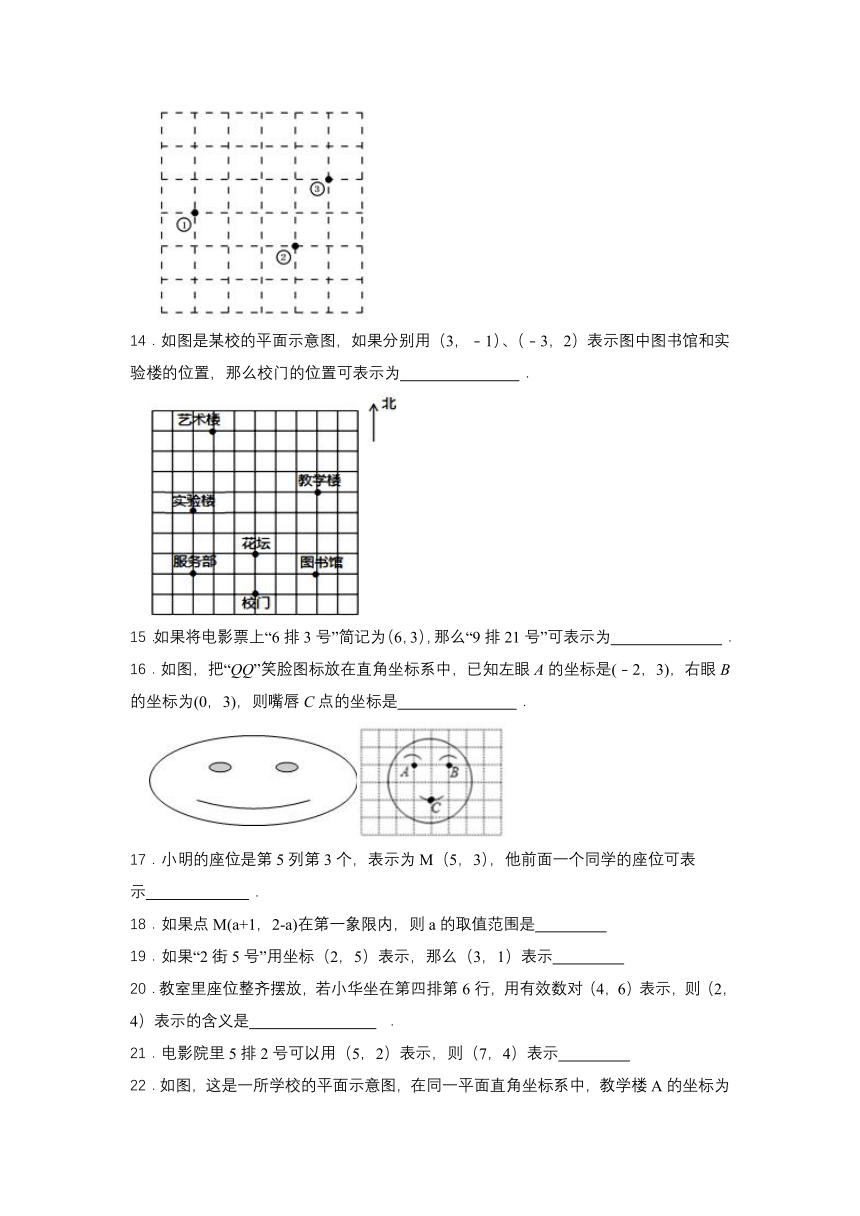
二、填空题
13.如图所示的棋盘放置在某个平面直角坐标系内,棋子①的坐标为 ,棋子②的坐标为 ,那么棋子③的坐标是 .
14.如图是某校的平面示意图,如果分别用(3,﹣1)、(﹣3,2)表示图中图书馆和实验楼的位置,那么校门的位置可表示为 .
15.如果将电影票上“6排3号”简记为(6,3),那么“9排21号”可表示为 .
16.如图,把“QQ”笑脸图标放在直角坐标系中,已知左眼A的坐标是(﹣2,3),右眼B的坐标为(0,3),则嘴唇C点的坐标是 .
17.小明的座位是第5列第3个,表示为M(5,3),他前面一个同学的座位可表示 .
18.如果点M(a+1,2-a)在第一象限内,则a的取值范围是
19.如果“2街5号”用坐标(2,5)表示,那么(3,1)表示
20.教室里座位整齐摆放,若小华坐在第四排第6行,用有效数对(4,6)表示,则(2,4)表示的含义是 .
21.电影院里5排2号可以用(5,2)表示,则(7,4)表示
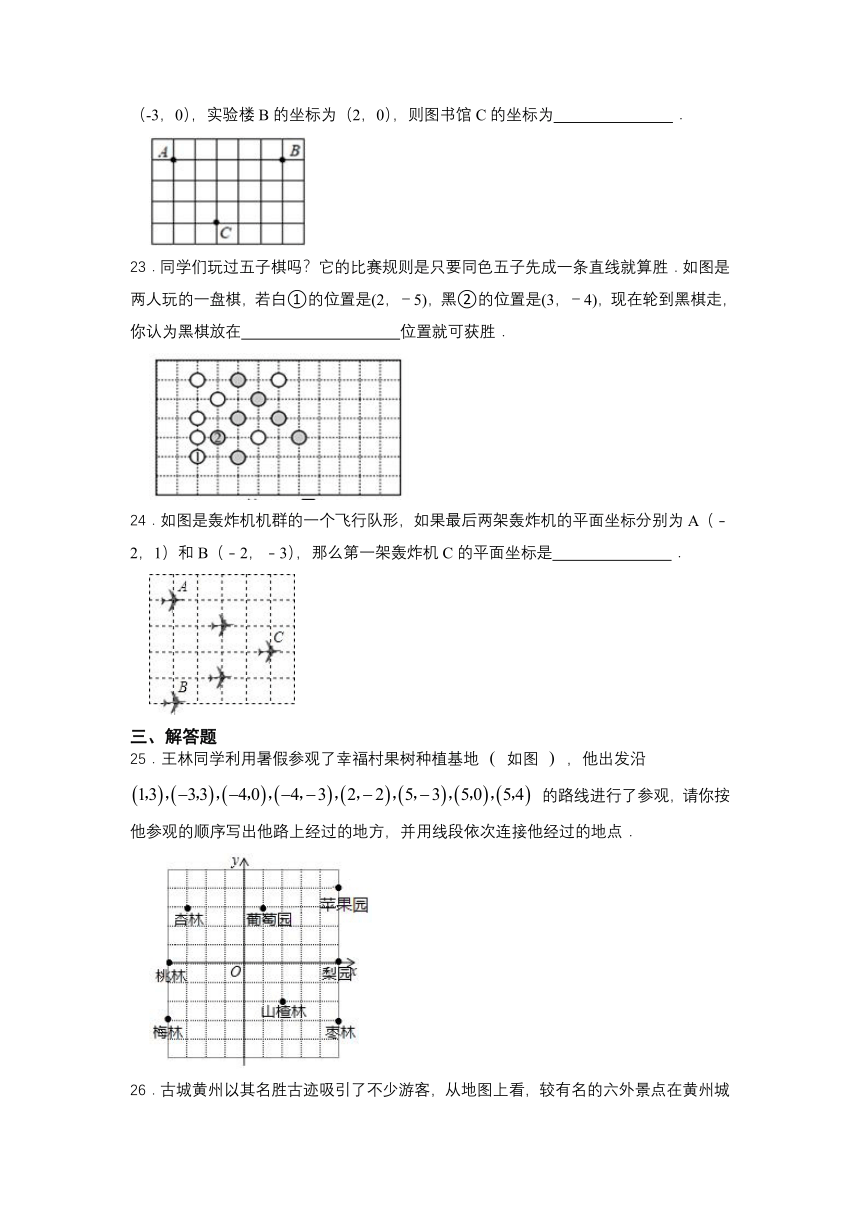
22.如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(-3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 .
23.同学们玩过五子棋吗?它的比赛规则是只要同色五子先成一条直线就算胜.如图是两人玩的一盘棋,若白①的位置是(2,-5),黑②的位置是(3,-4),现在轮到黑棋走,你认为黑棋放在 位置就可获胜.
24.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是 .
三、解答题
25.王林同学利用暑假参观了幸福村果树种植基地 如图 ,他出发沿 的路线进行了参观,请你按他参观的顺序写出他路上经过的地方,并用线段依次连接他经过的地点.
26.古城黄州以其名胜古迹吸引了不少游客,从地图上看,较有名的六外景点在黄州城内的分布是∶东坡赤壁在市政府以西2km再往南3km处,黄冈中学在市政府以东1km处,宝塔公园在市政府以东3km处,鄂黄大桥在市政府以东7km再往北8km处,遗爱湖在市政府以东4km再往北4km处,博物馆在市政府以北2km再往西1km处.请画图表示出这六个景点的位置,并用坐标表示出来.
27.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
28.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
29.五子连珠棋的棋盘是15行15列的正方形,规定黑子先下,双方交替进行,在任意一个方向上,先连成5个子的一方获胜,如图所示的是两人所下的棋局的一部分,A点的位置记作(8,3),执白子的一方若想再放一子便获胜,应该把子落在什么位置?
四、综合题
30.平面直角坐标系中,三角形ABC的顶点都在网格点上.
(1)平移三角形ABC,使点C与坐标原点O是对应点,请画出平移后的三角形A′B′C′;
(2)写出A,B两点的对应点A′,B′的坐标;
(3)请直接写出三角形ABC的面积.
31.如图,是某动物园的示意图,如果在分别以正东、正北方向为 轴、 轴正方向的直角坐标系中,猴山和狮虎山的坐标分别是 和 ;
(1)请在图中画出这个平面直角坐标系;
(2)写出表示鸟园和鹿园的点的坐标;
(3)在图中标出熊猫馆 的位置.
32.如图是某次海战中交战双方舰艇的对峙示意图,对甲方潜艇来说:
(1)北偏东40°的方向上有哪些目标?要想确定乙方战舰B的位置,还需要什么数据?
(2)距甲方潜艇图上距离为1 cm处的乙舰有哪几艘?
(3)要确定每艘乙舰的位置,各需几个数据?
答案解析部分
1.【答案】B
【考点】用坐标表示地理位置
【解析】【解答】以车站为原点,正东为x轴正方向,正北为y轴正方向,那么小红家的坐标为(400,500),小强家的坐标为(-200,500),所以小强家在小红家正西.
【分析】根据题意建立平面直角坐标系解题更直观.
2.【答案】C
【考点】用坐标表示地理位置
【解析】【解答】由题图可知A地的位置为东经140° ,北纬50°.
【分析】根据所给题图求解即可。
3.【答案】C
【考点】用坐标表示地理位置
【解析】【解答】解:选项A、B是用区域定位法确定位置;选项D是用经纬度定位法确定位置,只有选项C不能够物体的具体位置.
故答案为:C.
【分析】平面内确定物体位置的方法有:区域定位法、经纬度定位法、坐标定位法、方位角+距离定位法,据此判断.
4.【答案】D
【考点】用坐标表示地理位置
【解析】【解答】根据平方的意义可知 ,则 ,即可判断点P所在象限.
,
∴点P( +1,-2)在第四象限
故答案为:D.
【分析】因为+10,-20,所以点P在第四象限。选项D符合题意。
5.【答案】D
【考点】用坐标表示地理位置
【解析】【解答】解:因为xy=0,所以x、y中至少有一个是0;
当x=0时,点在y轴上;
当y=0时,点在x轴上;
∵x≠y,
∴x、y不能同时为0.
即P不能是原点,
所以点P的位置是在x轴上或在y轴上(除原点).
故选D.
6.【答案】C
【考点】用坐标表示地理位置
【解析】【解答】解:∵点的横坐标-2<0,纵坐标-1<0,
∴点(-2,-1)在第三象限.
故选C.
【分析】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
7.【答案】A
【考点】用坐标表示地理位置
【解析】【解答】解:A.我校八年级(1)班班级座位3排4列,能确定具体位置,故符合题意;
B.滨海县育才路,不能确定具体位置,故不符合题意;
C.东经118°,不能确定具体位置,故不符合题意;
D.县一中北偏东60°,不能确定具体位置,故不符合题意.
故答案为:A.
【分析】根据用点的坐标确定地理位置是用一对有序实数对表示,由此可排除B,C,D,即可得到答案。
8.【答案】B
【考点】用坐标表示地理位置
【解析】【解答】解:“帅”的位置向右平移1个单位,上移两个单位(0,0),
故选:B.
【分析】根据“帅”的位置向右平移1个单位,上移两个单位,可得答案.
9.【答案】C
【考点】用坐标表示地理位置
【解析】【分析】根据方向角确定坐标位置对各选项分析判断后利用排除法求【解答】
A、炎陵位于株洲市区南偏东约35°的方向上正确,故本选项错误;
B、醴陵位于攸县的北偏东约16°的方向上正确,故本选项错误;
C、应为株洲县位于茶陵的北偏西约40°的方向上,故本选项正确;
D、株洲市区位于攸县的北偏西约21°的方向上正确,故本选项错误。
故选C。
10.【答案】A
【考点】用坐标表示地理位置
【解析】【解答】解:由棋子“车”的坐标为(﹣2,3)、棋子“马”的坐标为(1,3)可知,平面直角坐标系的原点为底边正中间的点,以底边为x轴,向右为正方向,以左右正中间的线为y轴,向上为正方向;
根据得出的坐标系可知,棋子“炮”的坐标为(3,2).
故选:A.
【分析】根据已知两点的坐标确定符合条件的平面直角坐标系,然后确定其它点的坐标.
11.【答案】D
【考点】用坐标表示地理位置
【解析】【分析】直接利用刻度尺和量角器进行测量来判断.
【解答】通过测量,宿舍楼位置是D.
故选D.
【点评】本题主要考查了学生的动手操作能力、利用点的坐标解决实际问题的能力和阅读理解能力.
12.【答案】D
【考点】点的坐标;用坐标表示地理位置
【解析】【解答】解:由“ 位于点(1,﹣1)”知,y轴为从左向右数的第四条竖直直线,且向上为正方向,x轴是从上往下数第四条水平直线,这两条直线交点为坐标原点.那么“ ”的位置为(﹣3,2).
故选D.
【分析】根据的点的坐标,建立平面直角坐标系,从而确定的点的坐标即可。
13.【答案】(1,-1)
【考点】用坐标表示地理位置
【解析】【解答】根据①②的坐标可推出坐标系如下图所示,
故③的坐标为(1,-1).
【分析】根据①的坐标为 ,棋子②的坐标为 推出x轴和y轴的位置,即可得到③的坐标.
14.【答案】(0,﹣2)
【考点】用坐标表示地理位置
【解析】【解答】解:如图,校门的位置可表示为(0,﹣2).
故答案为:(0,﹣2).
【分析】由图书馆和实验楼的表示的坐标特点可以确定图书馆位于第一象限,实验楼位于第二象限,再由坐标的具体位置确定花坛为平面直角坐标系的原点,校门的位置随之可以确定。
15.【答案】(9,21)
【考点】用坐标表示地理位置
【解析】【解答】由“6排3号”简记为(6,3)可知:括号中的第一个数表示排数,第二个数表示号数,
∴“9排21号”可表示为(9,21).
故答案为:(9,21)
【分析】根据题中所给的“6排3号”点的坐标,即可得出“9排21号”点的坐标。
16.【答案】(-1,1)
【考点】用坐标表示地理位置
【解析】【解答】解:∵左眼A的坐标是(-2,3),右眼B的坐标为(0,3),
∴嘴唇C的坐标是(-1,1),
故答案为:(-1,1)
【分析】根据左眼,右眼坐标,得到嘴唇C的坐标
17.【答案】(5,2)
【考点】用坐标表示地理位置
【解析】【解答】解:他前面一个同学的座位为第5列第2个,表示为(5,2).故答案为:(5,2).
【分析】由平面直角坐标系的特征可知这两个同学的横坐标相同,小明的纵坐标比他前面一个同学的纵坐标大1,则他前面一个同学的座位可表示(5,2).
18.【答案】-1【考点】点的坐标;用坐标表示地理位置
【解析】【解答】解:∵点M(a+1,2-a)在第一象限,
∴a+1>0,2-a>0,
解得:-1<a<2.
19.【答案】3街1号
【考点】用坐标表示地理位置
【解析】【解答】解:∵“2街5号”用坐标(2,5)表示,
∴(3,1)表示“3街1号”.
故答案为:3街1号.
【分析】根据有序数对的两个数表示的含义解答即可.
20.【答案】第二排第4行
【考点】用坐标表示地理位置
【解析】【解答】解:∵小华坐在第四排第6行,用有效数对(4,6)表示,
∴(2,4)表示的含义是:第二排第4行.
故答案为:第二排第4行.
【分析】利用已知坐标中第一个数字为排,第二个数字为行,进而得出答案.
21.【答案】7排4号
【考点】用坐标表示地理位置
【解析】【解答】解:根据题意知:前一个数表示排数,后一个数表示号数,
则(7,4)的意义为第7排4号.
故答案为:7排4号.
【分析】由“5排2号”记作(5,2)可知,有序数对与排号对应,(7,4)的意义为第7排4号.
22.【答案】(-1,-3)
【考点】用坐标表示地理位置;平面直角坐标系的构成
【解析】【解答】解:如图所示:
图书馆C的坐标为(-1,-3).
故答案为:(-1,-3).
【分析】根据题意直接利用已知点坐标进而建立平面直角坐标系,即可得出C点坐标.
23.【答案】(3,0)或(8, 5)
【考点】用坐标表示地理位置
【解析】【解答】解:如图所示,黑棋放在图中三角形位置,就能获胜,
∵白①的位置是:(2, 5),黑②的位置是:(3, 4),
∴P点为坐标原点的位置,
∴黑棋放在(3,0)或(8, 5)位置就能获胜.
故答案为:(3,0)或(8, 5).
【分析】根据黑棋放在如图位置就获得胜利,再根据白①的位置是(2,-5),黑②的位置是(3,-4),即可求出两点的坐标.
24.【答案】(2,﹣1)
【考点】用坐标表示地理位置
【解析】【解答】解:因为A(﹣2,1)和B(﹣2,﹣3),
所以可得点C的坐标为(2,﹣1),
故答案为:(2,﹣1).
【分析】根据A(﹣2,1)和B(﹣2,﹣3)的坐标以及与C的关系进行解答即可.
25.【答案】解:由各点的坐标可知他路上经过的地方:葡萄园 杏林 桃林 梅林 山楂林 枣林 梨园 苹果园.
如图所示:
【考点】用坐标表示地理位置
【解析】【分析】由各点的坐标可知王林同学在路上经过的地方依次是:葡萄园 → 杏林 → 桃林 → 梅林 → 山楂林 → 枣林 → 梨园 → 苹果园.
26.【答案】解:如下图所示:
其坐标分别为∶东坡赤壁为(-2,-3),黄冈中学为(1,0),宝塔公园为(3,0),鄂黄大桥为(7,8),遗爱湖为(4,4),博物馆为(-1,2)
【考点】用坐标表示地理位置
【解析】【分析】考查建立平面直角坐标系,主要考查用坐标表示位置考点的理解.首先确定原点市政府,然后画出x,y轴,定单位长度为1km.根据题意描点即可.
27.【答案】解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,所以礼物为:我是最棒的;(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,所以礼物为:努力就能行;(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,所以礼物为:明天会更好.
【考点】用坐标表示地理位置
【解析】【分析】(1)根据表格,分别找出一1→三2→二4→四3→五1表示的汉字,排列即可;
(2)根据表格,分别找出五3→二1→二3→一5→三4表示的汉字,排列即可;
(3)根据表格,分别找出四5→四1→一2→三3→五2表示的汉字,排列即可.
28.【答案】(1)解:建立直角坐标系如图所示:
图书馆B位置的坐标为(-3,-2)。
(2)解:标出体育馆位置C如图所示,
观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为10.
【考点】用坐标表示地理位置
【解析】【分析】(1)利用已知的学校的坐标,找到原点,画出直角坐标系,观察写出B点的坐标。(2)求△ABC的面积,可利用坐标求出B到C点距离作为底,A点到BC的距离为高,进行计算。
29.【答案】解:连成一条直线就获胜,那么执白子的一方应该把子落在(0,2)或(5,7)处。
【考点】用坐标表示地理位置
【解析】【分析】根据五子棋的规则,只要同一棋子直接连成5子或连成4子且两端位置为空,可获胜,就可得出答案。
30.【答案】(1)解:如图所示,△A′B′C′即为所求作的三角形;
(2)解:点A′、B′的坐标分别为A′(1,﹣3)、B′(3,1)
(3)解:S△ABC=3×4﹣ ×3×1﹣ ×2×4﹣ ×1×3,
=12﹣ ﹣4﹣ ,
=12﹣7,
=5.
【考点】用坐标表示地理位置;坐标与图形变化﹣平移
【解析】【分析】根据平移的性质点C与坐标原点O是对应点,图形先向下平移2个单位长度,再向左平移1个单位长度,得到点A′、B′的坐标分别为A′(1,﹣3)、B′(3,1);三角形ABC的面积等于矩形面积减去其他三个图形面积即可.
31.【答案】(1)解:如图:
(2)鸟园 ,鹿园
(3)解:如图:
【考点】用坐标表示地理位置
【解析】【分析】(1)将表示狮虎山的点向下平移3个单位长度后的对应点作为坐标原点建立平面直角坐标系即可;
(2)根据坐标系写出鸟园和鹿园的点的坐标即可;
(3)直接在坐标轴中找到(2,-2)点即可.
32.【答案】(1)解:对甲方潜艇来说,北偏东40°的方向上有两个目标,乙方战舰B和小岛;要确定乙方战舰B的位置,还要知道乙方战舰到甲方潜艇的距离
(2)解:距甲方潜艇图上距离为1cm处的乙舰有两艘:乙方战舰A和乙方战舰C.
(3)解:要确定每艘乙舰的位置,各需两个数据:距离和方位角.如对甲方潜艇来说,乙方战舰A在正南方向,图上距离1cm处;乙方战舰B在北偏东40°方向,图上距离为1.2cm处;乙方战舰C在正东方向,图上距离为1 cm处.
【考点】用坐标表示地理位置
【解析】【分析】(1)由图知,北偏东40°的方向上的目标有:乙方战舰B和小岛;要确定乙方战舰B的位置,还要知道乙方战舰到甲方潜艇的距离;
(2)由图知,距甲方潜艇图上距离为1cm处的乙舰有乙方战舰A和乙方战舰C;
(3)在平面内,要确定一个点的位置,需要距离和方位角两个数据即可。
7.2.1用坐标表示地理位置靶向训练(含解析)
一、单选题
1.从车站向东走400米,再向北走500米到小红家;从车站向北走500米,向西走200米到小强家,则( )
A.小强家在小红家正东 B.小强家在小红家正西
C.小强家在小红家正南 D.小强家在小红家正北
2.A地在地球上的位置如图所示,则A地的位置是( )
A.东经130°,北纬50° B.东经130°,北纬60°
C.东经140°,北纬50° D.东经40°,北纬50°
3.下列数据中不能确定物体位置的是( )
A.某市政府位于北京路32号 B.小明住在某小区3号楼7号
C.太阳在我们的正上方 D.东经130°,北纬54°的城市
4.在平面直角坐标系中,点P( +1,-2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.若点P(x,y)的坐标满足xy=0(x≠y),则点P必在( )
A.原点上 B.x轴上
C.y轴上 D.x轴上或y轴上(除原点)
6.点 所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.根据下列表述,能确定具体位置的是( )
A.我校八年级(1)班班级座位3排4列
B.滨海县育才路
C.东经118°
D.县一中北偏东60°
8.如图,若在象棋盘上建立直角坐标系xOy,使“帥”位于点(﹣1,﹣2),“馬”位于点(2,﹣2),则“炮”位于点( )
A.(﹣2,﹣1) B.(0,0)
C.(1,﹣2) D.(﹣1,1)
9.如图是株洲市的行政区域平面地图,下列关于方位的说法明显错误的是
A.炎陵位于株洲市区南偏东约35°的方向上
B.醴陵位于攸县的北偏东约16°的方向上
C.株洲县位于茶陵的南偏东约40°的方向上
D.株洲市区位于攸县的北偏西约21°的方向上
10.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(3,2) B.(3,1)
C.(2,2) D.(﹣2,2)
11.如图是某中学的平面示意图,其中宿舍楼暂未标注,已知宿舍楼在教学楼的北偏东约30o的方向,与教学楼实际距离约为200米,试借助刻度尺和量角器,测量图中四点位置,能比较准确地表示该宿舍楼位置的是( )
A.点A B.点B
C.点C D.点D
12.如图是中国象棋棋盘的一部分,若 位于点(1,﹣1),则 位于点( )
A.(3,﹣2) B.(2,﹣3) C.(﹣2,3) D.(﹣3,2)
二、填空题
13.如图所示的棋盘放置在某个平面直角坐标系内,棋子①的坐标为 ,棋子②的坐标为 ,那么棋子③的坐标是 .
14.如图是某校的平面示意图,如果分别用(3,﹣1)、(﹣3,2)表示图中图书馆和实验楼的位置,那么校门的位置可表示为 .
15.如果将电影票上“6排3号”简记为(6,3),那么“9排21号”可表示为 .
16.如图,把“QQ”笑脸图标放在直角坐标系中,已知左眼A的坐标是(﹣2,3),右眼B的坐标为(0,3),则嘴唇C点的坐标是 .
17.小明的座位是第5列第3个,表示为M(5,3),他前面一个同学的座位可表示 .
18.如果点M(a+1,2-a)在第一象限内,则a的取值范围是
19.如果“2街5号”用坐标(2,5)表示,那么(3,1)表示
20.教室里座位整齐摆放,若小华坐在第四排第6行,用有效数对(4,6)表示,则(2,4)表示的含义是 .
21.电影院里5排2号可以用(5,2)表示,则(7,4)表示
22.如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(-3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 .
23.同学们玩过五子棋吗?它的比赛规则是只要同色五子先成一条直线就算胜.如图是两人玩的一盘棋,若白①的位置是(2,-5),黑②的位置是(3,-4),现在轮到黑棋走,你认为黑棋放在 位置就可获胜.
24.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是 .
三、解答题
25.王林同学利用暑假参观了幸福村果树种植基地 如图 ,他出发沿 的路线进行了参观,请你按他参观的顺序写出他路上经过的地方,并用线段依次连接他经过的地点.
26.古城黄州以其名胜古迹吸引了不少游客,从地图上看,较有名的六外景点在黄州城内的分布是∶东坡赤壁在市政府以西2km再往南3km处,黄冈中学在市政府以东1km处,宝塔公园在市政府以东3km处,鄂黄大桥在市政府以东7km再往北8km处,遗爱湖在市政府以东4km再往北4km处,博物馆在市政府以北2km再往西1km处.请画图表示出这六个景点的位置,并用坐标表示出来.
27.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
28.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
29.五子连珠棋的棋盘是15行15列的正方形,规定黑子先下,双方交替进行,在任意一个方向上,先连成5个子的一方获胜,如图所示的是两人所下的棋局的一部分,A点的位置记作(8,3),执白子的一方若想再放一子便获胜,应该把子落在什么位置?
四、综合题
30.平面直角坐标系中,三角形ABC的顶点都在网格点上.
(1)平移三角形ABC,使点C与坐标原点O是对应点,请画出平移后的三角形A′B′C′;
(2)写出A,B两点的对应点A′,B′的坐标;
(3)请直接写出三角形ABC的面积.
31.如图,是某动物园的示意图,如果在分别以正东、正北方向为 轴、 轴正方向的直角坐标系中,猴山和狮虎山的坐标分别是 和 ;
(1)请在图中画出这个平面直角坐标系;
(2)写出表示鸟园和鹿园的点的坐标;
(3)在图中标出熊猫馆 的位置.
32.如图是某次海战中交战双方舰艇的对峙示意图,对甲方潜艇来说:
(1)北偏东40°的方向上有哪些目标?要想确定乙方战舰B的位置,还需要什么数据?
(2)距甲方潜艇图上距离为1 cm处的乙舰有哪几艘?
(3)要确定每艘乙舰的位置,各需几个数据?
答案解析部分
1.【答案】B
【考点】用坐标表示地理位置
【解析】【解答】以车站为原点,正东为x轴正方向,正北为y轴正方向,那么小红家的坐标为(400,500),小强家的坐标为(-200,500),所以小强家在小红家正西.
【分析】根据题意建立平面直角坐标系解题更直观.
2.【答案】C
【考点】用坐标表示地理位置
【解析】【解答】由题图可知A地的位置为东经140° ,北纬50°.
【分析】根据所给题图求解即可。
3.【答案】C
【考点】用坐标表示地理位置
【解析】【解答】解:选项A、B是用区域定位法确定位置;选项D是用经纬度定位法确定位置,只有选项C不能够物体的具体位置.
故答案为:C.
【分析】平面内确定物体位置的方法有:区域定位法、经纬度定位法、坐标定位法、方位角+距离定位法,据此判断.
4.【答案】D
【考点】用坐标表示地理位置
【解析】【解答】根据平方的意义可知 ,则 ,即可判断点P所在象限.
,
∴点P( +1,-2)在第四象限
故答案为:D.
【分析】因为+10,-20,所以点P在第四象限。选项D符合题意。
5.【答案】D
【考点】用坐标表示地理位置
【解析】【解答】解:因为xy=0,所以x、y中至少有一个是0;
当x=0时,点在y轴上;
当y=0时,点在x轴上;
∵x≠y,
∴x、y不能同时为0.
即P不能是原点,
所以点P的位置是在x轴上或在y轴上(除原点).
故选D.
6.【答案】C
【考点】用坐标表示地理位置
【解析】【解答】解:∵点的横坐标-2<0,纵坐标-1<0,
∴点(-2,-1)在第三象限.
故选C.
【分析】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
7.【答案】A
【考点】用坐标表示地理位置
【解析】【解答】解:A.我校八年级(1)班班级座位3排4列,能确定具体位置,故符合题意;
B.滨海县育才路,不能确定具体位置,故不符合题意;
C.东经118°,不能确定具体位置,故不符合题意;
D.县一中北偏东60°,不能确定具体位置,故不符合题意.
故答案为:A.
【分析】根据用点的坐标确定地理位置是用一对有序实数对表示,由此可排除B,C,D,即可得到答案。
8.【答案】B
【考点】用坐标表示地理位置
【解析】【解答】解:“帅”的位置向右平移1个单位,上移两个单位(0,0),
故选:B.
【分析】根据“帅”的位置向右平移1个单位,上移两个单位,可得答案.
9.【答案】C
【考点】用坐标表示地理位置
【解析】【分析】根据方向角确定坐标位置对各选项分析判断后利用排除法求【解答】
A、炎陵位于株洲市区南偏东约35°的方向上正确,故本选项错误;
B、醴陵位于攸县的北偏东约16°的方向上正确,故本选项错误;
C、应为株洲县位于茶陵的北偏西约40°的方向上,故本选项正确;
D、株洲市区位于攸县的北偏西约21°的方向上正确,故本选项错误。
故选C。
10.【答案】A
【考点】用坐标表示地理位置
【解析】【解答】解:由棋子“车”的坐标为(﹣2,3)、棋子“马”的坐标为(1,3)可知,平面直角坐标系的原点为底边正中间的点,以底边为x轴,向右为正方向,以左右正中间的线为y轴,向上为正方向;
根据得出的坐标系可知,棋子“炮”的坐标为(3,2).
故选:A.
【分析】根据已知两点的坐标确定符合条件的平面直角坐标系,然后确定其它点的坐标.
11.【答案】D
【考点】用坐标表示地理位置
【解析】【分析】直接利用刻度尺和量角器进行测量来判断.
【解答】通过测量,宿舍楼位置是D.
故选D.
【点评】本题主要考查了学生的动手操作能力、利用点的坐标解决实际问题的能力和阅读理解能力.
12.【答案】D
【考点】点的坐标;用坐标表示地理位置
【解析】【解答】解:由“ 位于点(1,﹣1)”知,y轴为从左向右数的第四条竖直直线,且向上为正方向,x轴是从上往下数第四条水平直线,这两条直线交点为坐标原点.那么“ ”的位置为(﹣3,2).
故选D.
【分析】根据的点的坐标,建立平面直角坐标系,从而确定的点的坐标即可。
13.【答案】(1,-1)
【考点】用坐标表示地理位置
【解析】【解答】根据①②的坐标可推出坐标系如下图所示,
故③的坐标为(1,-1).
【分析】根据①的坐标为 ,棋子②的坐标为 推出x轴和y轴的位置,即可得到③的坐标.
14.【答案】(0,﹣2)
【考点】用坐标表示地理位置
【解析】【解答】解:如图,校门的位置可表示为(0,﹣2).
故答案为:(0,﹣2).
【分析】由图书馆和实验楼的表示的坐标特点可以确定图书馆位于第一象限,实验楼位于第二象限,再由坐标的具体位置确定花坛为平面直角坐标系的原点,校门的位置随之可以确定。
15.【答案】(9,21)
【考点】用坐标表示地理位置
【解析】【解答】由“6排3号”简记为(6,3)可知:括号中的第一个数表示排数,第二个数表示号数,
∴“9排21号”可表示为(9,21).
故答案为:(9,21)
【分析】根据题中所给的“6排3号”点的坐标,即可得出“9排21号”点的坐标。
16.【答案】(-1,1)
【考点】用坐标表示地理位置
【解析】【解答】解:∵左眼A的坐标是(-2,3),右眼B的坐标为(0,3),
∴嘴唇C的坐标是(-1,1),
故答案为:(-1,1)
【分析】根据左眼,右眼坐标,得到嘴唇C的坐标
17.【答案】(5,2)
【考点】用坐标表示地理位置
【解析】【解答】解:他前面一个同学的座位为第5列第2个,表示为(5,2).故答案为:(5,2).
【分析】由平面直角坐标系的特征可知这两个同学的横坐标相同,小明的纵坐标比他前面一个同学的纵坐标大1,则他前面一个同学的座位可表示(5,2).
18.【答案】-1
【解析】【解答】解:∵点M(a+1,2-a)在第一象限,
∴a+1>0,2-a>0,
解得:-1<a<2.
19.【答案】3街1号
【考点】用坐标表示地理位置
【解析】【解答】解:∵“2街5号”用坐标(2,5)表示,
∴(3,1)表示“3街1号”.
故答案为:3街1号.
【分析】根据有序数对的两个数表示的含义解答即可.
20.【答案】第二排第4行
【考点】用坐标表示地理位置
【解析】【解答】解:∵小华坐在第四排第6行,用有效数对(4,6)表示,
∴(2,4)表示的含义是:第二排第4行.
故答案为:第二排第4行.
【分析】利用已知坐标中第一个数字为排,第二个数字为行,进而得出答案.
21.【答案】7排4号
【考点】用坐标表示地理位置
【解析】【解答】解:根据题意知:前一个数表示排数,后一个数表示号数,
则(7,4)的意义为第7排4号.
故答案为:7排4号.
【分析】由“5排2号”记作(5,2)可知,有序数对与排号对应,(7,4)的意义为第7排4号.
22.【答案】(-1,-3)
【考点】用坐标表示地理位置;平面直角坐标系的构成
【解析】【解答】解:如图所示:
图书馆C的坐标为(-1,-3).
故答案为:(-1,-3).
【分析】根据题意直接利用已知点坐标进而建立平面直角坐标系,即可得出C点坐标.
23.【答案】(3,0)或(8, 5)
【考点】用坐标表示地理位置
【解析】【解答】解:如图所示,黑棋放在图中三角形位置,就能获胜,
∵白①的位置是:(2, 5),黑②的位置是:(3, 4),
∴P点为坐标原点的位置,
∴黑棋放在(3,0)或(8, 5)位置就能获胜.
故答案为:(3,0)或(8, 5).
【分析】根据黑棋放在如图位置就获得胜利,再根据白①的位置是(2,-5),黑②的位置是(3,-4),即可求出两点的坐标.
24.【答案】(2,﹣1)
【考点】用坐标表示地理位置
【解析】【解答】解:因为A(﹣2,1)和B(﹣2,﹣3),
所以可得点C的坐标为(2,﹣1),
故答案为:(2,﹣1).
【分析】根据A(﹣2,1)和B(﹣2,﹣3)的坐标以及与C的关系进行解答即可.
25.【答案】解:由各点的坐标可知他路上经过的地方:葡萄园 杏林 桃林 梅林 山楂林 枣林 梨园 苹果园.
如图所示:
【考点】用坐标表示地理位置
【解析】【分析】由各点的坐标可知王林同学在路上经过的地方依次是:葡萄园 → 杏林 → 桃林 → 梅林 → 山楂林 → 枣林 → 梨园 → 苹果园.
26.【答案】解:如下图所示:
其坐标分别为∶东坡赤壁为(-2,-3),黄冈中学为(1,0),宝塔公园为(3,0),鄂黄大桥为(7,8),遗爱湖为(4,4),博物馆为(-1,2)
【考点】用坐标表示地理位置
【解析】【分析】考查建立平面直角坐标系,主要考查用坐标表示位置考点的理解.首先确定原点市政府,然后画出x,y轴,定单位长度为1km.根据题意描点即可.
27.【答案】解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,所以礼物为:我是最棒的;(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,所以礼物为:努力就能行;(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,所以礼物为:明天会更好.
【考点】用坐标表示地理位置
【解析】【分析】(1)根据表格,分别找出一1→三2→二4→四3→五1表示的汉字,排列即可;
(2)根据表格,分别找出五3→二1→二3→一5→三4表示的汉字,排列即可;
(3)根据表格,分别找出四5→四1→一2→三3→五2表示的汉字,排列即可.
28.【答案】(1)解:建立直角坐标系如图所示:
图书馆B位置的坐标为(-3,-2)。
(2)解:标出体育馆位置C如图所示,
观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为10.
【考点】用坐标表示地理位置
【解析】【分析】(1)利用已知的学校的坐标,找到原点,画出直角坐标系,观察写出B点的坐标。(2)求△ABC的面积,可利用坐标求出B到C点距离作为底,A点到BC的距离为高,进行计算。
29.【答案】解:连成一条直线就获胜,那么执白子的一方应该把子落在(0,2)或(5,7)处。
【考点】用坐标表示地理位置
【解析】【分析】根据五子棋的规则,只要同一棋子直接连成5子或连成4子且两端位置为空,可获胜,就可得出答案。
30.【答案】(1)解:如图所示,△A′B′C′即为所求作的三角形;
(2)解:点A′、B′的坐标分别为A′(1,﹣3)、B′(3,1)
(3)解:S△ABC=3×4﹣ ×3×1﹣ ×2×4﹣ ×1×3,
=12﹣ ﹣4﹣ ,
=12﹣7,
=5.
【考点】用坐标表示地理位置;坐标与图形变化﹣平移
【解析】【分析】根据平移的性质点C与坐标原点O是对应点,图形先向下平移2个单位长度,再向左平移1个单位长度,得到点A′、B′的坐标分别为A′(1,﹣3)、B′(3,1);三角形ABC的面积等于矩形面积减去其他三个图形面积即可.
31.【答案】(1)解:如图:
(2)鸟园 ,鹿园
(3)解:如图:
【考点】用坐标表示地理位置
【解析】【分析】(1)将表示狮虎山的点向下平移3个单位长度后的对应点作为坐标原点建立平面直角坐标系即可;
(2)根据坐标系写出鸟园和鹿园的点的坐标即可;
(3)直接在坐标轴中找到(2,-2)点即可.
32.【答案】(1)解:对甲方潜艇来说,北偏东40°的方向上有两个目标,乙方战舰B和小岛;要确定乙方战舰B的位置,还要知道乙方战舰到甲方潜艇的距离
(2)解:距甲方潜艇图上距离为1cm处的乙舰有两艘:乙方战舰A和乙方战舰C.
(3)解:要确定每艘乙舰的位置,各需两个数据:距离和方位角.如对甲方潜艇来说,乙方战舰A在正南方向,图上距离1cm处;乙方战舰B在北偏东40°方向,图上距离为1.2cm处;乙方战舰C在正东方向,图上距离为1 cm处.
【考点】用坐标表示地理位置
【解析】【分析】(1)由图知,北偏东40°的方向上的目标有:乙方战舰B和小岛;要确定乙方战舰B的位置,还要知道乙方战舰到甲方潜艇的距离;
(2)由图知,距甲方潜艇图上距离为1cm处的乙舰有乙方战舰A和乙方战舰C;
(3)在平面内,要确定一个点的位置,需要距离和方位角两个数据即可。
