2021-2022学年北师大版九年级数学下册3.2圆的对称性自主提升训练(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性自主提升训练(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 195.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 20:53:32 | ||
图片预览


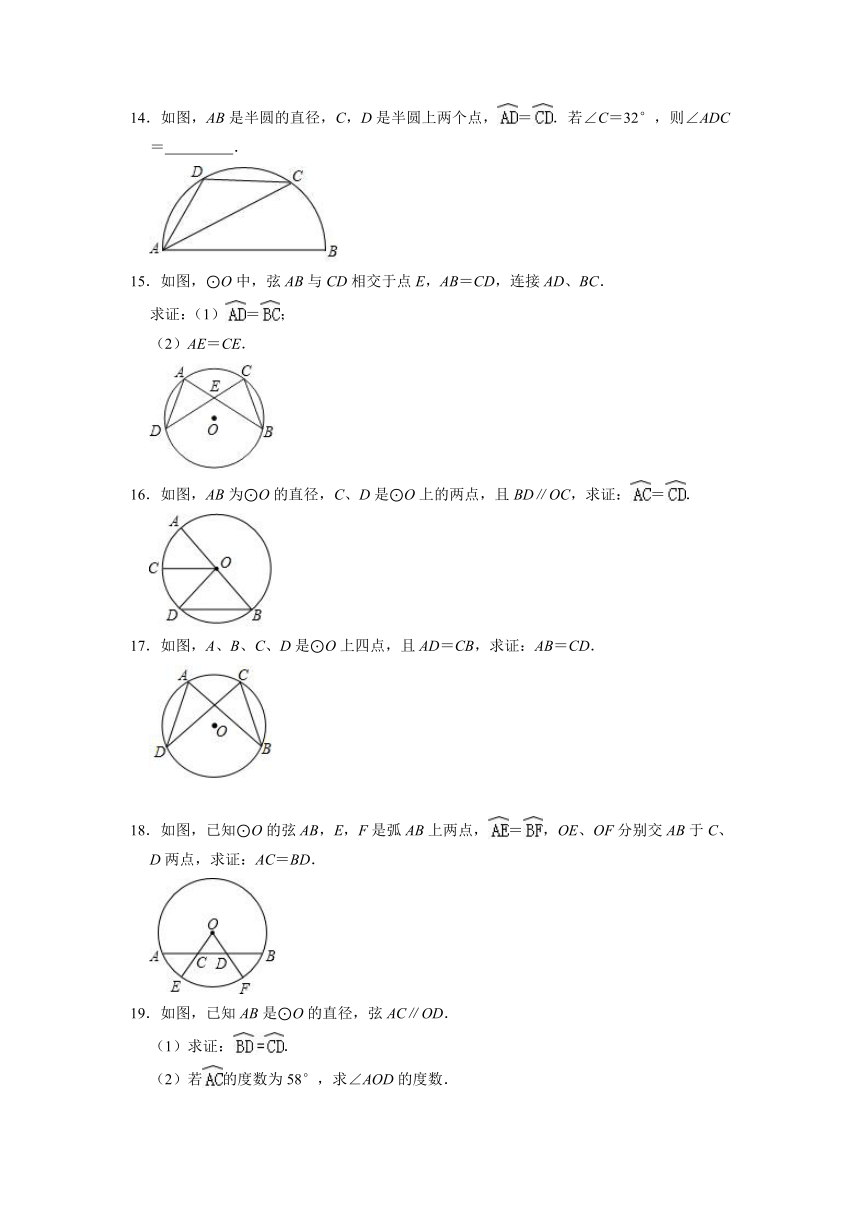

文档简介
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》同步自主提升训练(附答案)
1.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=100°,AD∥OC,则∠AOD=( )
A.20° B.60° C.50° D.40°
2.在同圆中,若AB=2CD,则与2的大小关系是( )
A.>2 B.<2 C.=2 D.不能确定
3.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
4.如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么与的数量关系是( )
A.= B.> C.< D.无法确定
5.将一个圆分成四个扇形,它们的圆心角的度数比为4:4:5:7,则这四个扇形中,圆心角最大的是( )
A.54° B.72° C.90° D.126°
6.在半径为1的圆中,长度等于的弦所对的弧的度数为( )
A.90° B.145° C.270° D.90°或270°
7.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为( )
A.25° B.30° C.50° D.65°
8.圆中有两条等弦AB=AE,夹角∠A=88°,延长AE到C,使EC=BE,连接BC,如图.则∠ABC的度数是( )
A.90° B.80° C.69° D.65°
9.下列命题中,正确的是( )
①顶点在圆心的角是圆心角;②相等的圆心角,所对的弧也相等;③两条弦相等,它们所对的弧也相等;④在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.①和③ C.①和④ D.①、②、③、④
10.如图,已知AB是⊙O的直径,=,则下列结论中正确的是( )
A.AC=OD B.AC∥OD C.= D.=
11.如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C.如果BC=OE,∠C=40°,求∠EOA= 度.
12.如图,AB是半圆的直径,O是圆心,=2,则∠ABC= 度.
13.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= .
14.如图,AB是半圆的直径,C,D是半圆上两个点,=.若∠C=32°,则∠ADC= .
15.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;
(2)AE=CE.
16.如图,AB为⊙O的直径,C、D是⊙O上的两点,且BD∥OC,求证:=.
17.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
18.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交AB于C、D两点,求证:AC=BD.
19.如图,已知AB是⊙O的直径,弦AC∥OD.
(1)求证:.
(2)若的度数为58°,求∠AOD的度数.
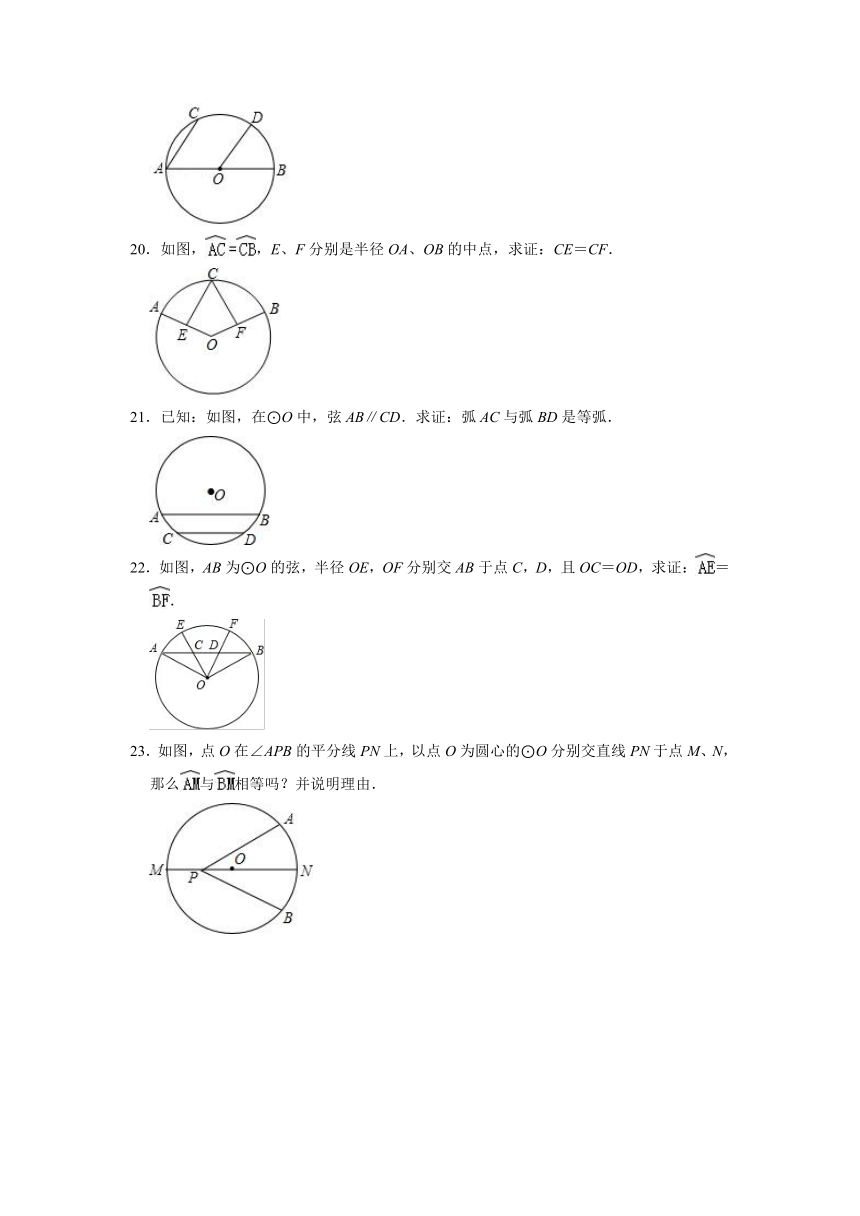
20.如图,,E、F分别是半径OA、OB的中点,求证:CE=CF.
21.已知:如图,在⊙O中,弦AB∥CD.求证:弧AC与弧BD是等弧.
22.如图,AB为⊙O的弦,半径OE,OF分别交AB于点C,D,且OC=OD,求证:=.
23.如图,点O在∠APB的平分线PN上,以点O为圆心的⊙O分别交直线PN于点M、N,那么与相等吗?并说明理由.
参考答案
1.解:∵∠BOC=100°,∠BOC+∠AOC=180°,
∴∠AOC=80°,
∵AD∥OC,OD=OA,
∴∠D=∠A=∠AOC=80°,
∴∠AOD=180°﹣2∠A=20°.
故选:A.
2.解:如图所示,CD=DE,AB=2CD,
在△CDE中,
∵CD=DE,
∴CE<CD+DE,即CE<2CD=AB,
∴CE<AB,
∴2<.
故选:A.
3.解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
4.证明:连接AC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴=.
故选:A.
5.解:设四个扇形的圆心角的度数是4x,4x,5x,7x,
得出方程4x+4x+5x+7x=360,
解得:x=18,
故7×18=126°.
故选:D.
6.解:如图,连接OA、OB;
∵在⊙O中,AB=,OA=OB=1,
∴AB2=OA2+OB2,
∴△AOB为直角三角形,且∠AOB=90°,
即长度等于的弦所对的弧长有两段:一段所对圆心角为90°,另一段所对圆心角为270°,
∴长度等于的弦所对的弧的度数为90°或270°.
故选:D.
7.解:连接CD,
∵在△ABC中,∠C=90°,∠A=25°,
∴∠ABC=90°﹣25°=65°,
∵BC=CD,
∴∠CDB=∠ABC=65°,
∴∠BCD=180°﹣∠CDB﹣∠CBD=180°﹣65°﹣65°=50°,
∴=50°.
故选:C.
8.解:∵AB=AE,EC=BE,
∴∠ABE=∠AEB,∠EBC=∠ACB,
又∵∠A=88°,
∴∠ABE=∠AEB=46°,∠EBC=∠ACB=∠AEB=23°,
∴∠ABC=∠ABE+∠EBC=69°.
故选:C.
9.解:①根据圆心角的定义知,顶点在圆心的角是圆心角;故①正确.
②缺少条件,必须是在同圆或等圆中,相等的圆心角所对的弧才相等;故错误.
③在圆中,一条弦对着两条弧,所以两条弦相等,它们所对的弧不一定相等;故错误.
④根据圆心角、弦、弧之间的关系定理,在等圆中,若圆心角相等,则弦相等,所以圆心角不等,弦也不等;故④正确.
故选:C.
10.解:∵=,
∴∠1=∠2,
∵∠BOC=∠A+∠C,
∵OA=OC,
∴∠A=∠C,
∴∠1=∠A,
∴AC∥OD.
故选:B.
11.解:连接OB,
∵OB=OE=BC,∠C=40°,
∴∠COB=∠C=40°,
∴∠ABO=∠C+∠COB=80°,
∵OA=OB,
∴∠A=∠ABO=80°,
△AOC中,∠EOA=180°﹣40°﹣80°=60°,
故答案为:60.
12.解:∵AB是半圆的直径,O是圆心,
∴∠AOB=180°;
又∵=2,
∴2∠AOC=∠BOC,
∴∠BOC=120°;
∵OB=OC(⊙O的半径),
∴∠OBC=∠OCB(等边对等角);
∴∠BOC+∠OBC+∠OCB=2∠ABC+∠COB=180°(三角形内角和定理),
∴∠ABC=30°.
故答案是:30°.
13.解:连接OM,ON,OA,OC,
∵M、N分别为AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴AM=AB,CN=CD,
∵∠AMN=∠CNM,
∴∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
,
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
∴AB=CD=6.
故答案是:6.
14.解:∵=,∠C=32°,
∴∠A=∠C=32°,
∴∠ADC=180°﹣∠A﹣∠C=180°﹣32°﹣32°=116°.
故答案为:116°.
15.证明(1)∵AB=CD,
∴=,即+=+,
∴=;
(2)由(1)知=,
∴AD=BC,
∵=,=,
∴∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
16.证明:∵OB=OD,
∴∠D=∠B,
∵BD∥OC,
∴∠D=∠COD,∠AOC=∠B,
∴∠AOC=∠COD,
∴=.
17.证明:∵AD=CB,
∴=,
∴+=+,
即=,
∴AB=CD.
18.证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵=,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD.
19.解:(1)连接OC.∵OA=OC,
∴∠OAC=∠ACO.
∵AC∥OD,
∴∠OAC=∠BOD.
∴∠DOC=∠ACO.
∴∠BOD=∠COD,
∴=.
(2)∵=,
∴==
∴∠BOD=∠BOC=(180°﹣58°)=61°.
∴∠AOD=58°+61°=119°
20.证明:连接OC.
在⊙O中,∵,
∴∠AOC=∠BOC,
∵OA=OB,E、F分别是半径OA、OB的中点,
∴OE=OF,
在△COE和△COF中,
,
∴△COE≌△COF(SAS),
∴CE=CF(全等三角形的对应边相等).
21.证明:连接OA、OC、OD、OB,如图,
∵OC=OD,
∴∠C=∠D,
∵AB∥CD,
∴∠1=∠C,∠2=∠D,
∴∠1=∠2,
∵∠1=∠A+∠AOC,∠2=∠B+∠BOD,
而OA=OB,
∴∠A=∠B,
∴∠AOC=∠BOD,
∴弧AC与弧BD是等弧
22.证明:过点O作OG⊥AB于点G,延长OG与⊙O交于H.
∵OC=OD,OG⊥CD于点G,
∴∠COG=∠DOG,
∴=.
又∵OG⊥AB于点G,
∴=,
∴﹣=﹣,
即=.
23.解:与相等,理由如下:
连接OA,OB,过点O作OE⊥PA于E,OF⊥PB于F.
∴点O在∠APB的平分线PN上,
∴OE=OF,
∵∠OEA=∠OFB=90°,
在Rt△OEA和Rt△OFB中,
,
∴Rt△OEA≌Rt△OFB(HL),
∴∠A=∠B,
∵∠AON=∠APO+∠A,∠BON=∠BPN+∠B
∴∠AON=∠BON,
∴∠AOM=∠BOM,
∴=.
1.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=100°,AD∥OC,则∠AOD=( )
A.20° B.60° C.50° D.40°
2.在同圆中,若AB=2CD,则与2的大小关系是( )
A.>2 B.<2 C.=2 D.不能确定
3.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
4.如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么与的数量关系是( )
A.= B.> C.< D.无法确定
5.将一个圆分成四个扇形,它们的圆心角的度数比为4:4:5:7,则这四个扇形中,圆心角最大的是( )
A.54° B.72° C.90° D.126°
6.在半径为1的圆中,长度等于的弦所对的弧的度数为( )
A.90° B.145° C.270° D.90°或270°
7.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为( )
A.25° B.30° C.50° D.65°
8.圆中有两条等弦AB=AE,夹角∠A=88°,延长AE到C,使EC=BE,连接BC,如图.则∠ABC的度数是( )
A.90° B.80° C.69° D.65°
9.下列命题中,正确的是( )
①顶点在圆心的角是圆心角;②相等的圆心角,所对的弧也相等;③两条弦相等,它们所对的弧也相等;④在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.①和③ C.①和④ D.①、②、③、④
10.如图,已知AB是⊙O的直径,=,则下列结论中正确的是( )
A.AC=OD B.AC∥OD C.= D.=
11.如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C.如果BC=OE,∠C=40°,求∠EOA= 度.
12.如图,AB是半圆的直径,O是圆心,=2,则∠ABC= 度.
13.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= .
14.如图,AB是半圆的直径,C,D是半圆上两个点,=.若∠C=32°,则∠ADC= .
15.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;
(2)AE=CE.
16.如图,AB为⊙O的直径,C、D是⊙O上的两点,且BD∥OC,求证:=.
17.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
18.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交AB于C、D两点,求证:AC=BD.
19.如图,已知AB是⊙O的直径,弦AC∥OD.
(1)求证:.
(2)若的度数为58°,求∠AOD的度数.
20.如图,,E、F分别是半径OA、OB的中点,求证:CE=CF.
21.已知:如图,在⊙O中,弦AB∥CD.求证:弧AC与弧BD是等弧.
22.如图,AB为⊙O的弦,半径OE,OF分别交AB于点C,D,且OC=OD,求证:=.
23.如图,点O在∠APB的平分线PN上,以点O为圆心的⊙O分别交直线PN于点M、N,那么与相等吗?并说明理由.
参考答案
1.解:∵∠BOC=100°,∠BOC+∠AOC=180°,
∴∠AOC=80°,
∵AD∥OC,OD=OA,
∴∠D=∠A=∠AOC=80°,
∴∠AOD=180°﹣2∠A=20°.
故选:A.
2.解:如图所示,CD=DE,AB=2CD,
在△CDE中,
∵CD=DE,
∴CE<CD+DE,即CE<2CD=AB,
∴CE<AB,
∴2<.
故选:A.
3.解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
4.证明:连接AC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴=.
故选:A.
5.解:设四个扇形的圆心角的度数是4x,4x,5x,7x,
得出方程4x+4x+5x+7x=360,
解得:x=18,
故7×18=126°.
故选:D.
6.解:如图,连接OA、OB;
∵在⊙O中,AB=,OA=OB=1,
∴AB2=OA2+OB2,
∴△AOB为直角三角形,且∠AOB=90°,
即长度等于的弦所对的弧长有两段:一段所对圆心角为90°,另一段所对圆心角为270°,
∴长度等于的弦所对的弧的度数为90°或270°.
故选:D.
7.解:连接CD,
∵在△ABC中,∠C=90°,∠A=25°,
∴∠ABC=90°﹣25°=65°,
∵BC=CD,
∴∠CDB=∠ABC=65°,
∴∠BCD=180°﹣∠CDB﹣∠CBD=180°﹣65°﹣65°=50°,
∴=50°.
故选:C.
8.解:∵AB=AE,EC=BE,
∴∠ABE=∠AEB,∠EBC=∠ACB,
又∵∠A=88°,
∴∠ABE=∠AEB=46°,∠EBC=∠ACB=∠AEB=23°,
∴∠ABC=∠ABE+∠EBC=69°.
故选:C.
9.解:①根据圆心角的定义知,顶点在圆心的角是圆心角;故①正确.
②缺少条件,必须是在同圆或等圆中,相等的圆心角所对的弧才相等;故错误.
③在圆中,一条弦对着两条弧,所以两条弦相等,它们所对的弧不一定相等;故错误.
④根据圆心角、弦、弧之间的关系定理,在等圆中,若圆心角相等,则弦相等,所以圆心角不等,弦也不等;故④正确.
故选:C.
10.解:∵=,
∴∠1=∠2,
∵∠BOC=∠A+∠C,
∵OA=OC,
∴∠A=∠C,
∴∠1=∠A,
∴AC∥OD.
故选:B.
11.解:连接OB,
∵OB=OE=BC,∠C=40°,
∴∠COB=∠C=40°,
∴∠ABO=∠C+∠COB=80°,
∵OA=OB,
∴∠A=∠ABO=80°,
△AOC中,∠EOA=180°﹣40°﹣80°=60°,
故答案为:60.
12.解:∵AB是半圆的直径,O是圆心,
∴∠AOB=180°;
又∵=2,
∴2∠AOC=∠BOC,
∴∠BOC=120°;
∵OB=OC(⊙O的半径),
∴∠OBC=∠OCB(等边对等角);
∴∠BOC+∠OBC+∠OCB=2∠ABC+∠COB=180°(三角形内角和定理),
∴∠ABC=30°.
故答案是:30°.
13.解:连接OM,ON,OA,OC,
∵M、N分别为AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴AM=AB,CN=CD,
∵∠AMN=∠CNM,
∴∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
,
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
∴AB=CD=6.
故答案是:6.
14.解:∵=,∠C=32°,
∴∠A=∠C=32°,
∴∠ADC=180°﹣∠A﹣∠C=180°﹣32°﹣32°=116°.
故答案为:116°.
15.证明(1)∵AB=CD,
∴=,即+=+,
∴=;
(2)由(1)知=,
∴AD=BC,
∵=,=,
∴∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
16.证明:∵OB=OD,
∴∠D=∠B,
∵BD∥OC,
∴∠D=∠COD,∠AOC=∠B,
∴∠AOC=∠COD,
∴=.
17.证明:∵AD=CB,
∴=,
∴+=+,
即=,
∴AB=CD.
18.证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵=,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD.
19.解:(1)连接OC.∵OA=OC,
∴∠OAC=∠ACO.
∵AC∥OD,
∴∠OAC=∠BOD.
∴∠DOC=∠ACO.
∴∠BOD=∠COD,
∴=.
(2)∵=,
∴==
∴∠BOD=∠BOC=(180°﹣58°)=61°.
∴∠AOD=58°+61°=119°
20.证明:连接OC.
在⊙O中,∵,
∴∠AOC=∠BOC,
∵OA=OB,E、F分别是半径OA、OB的中点,
∴OE=OF,
在△COE和△COF中,
,
∴△COE≌△COF(SAS),
∴CE=CF(全等三角形的对应边相等).
21.证明:连接OA、OC、OD、OB,如图,
∵OC=OD,
∴∠C=∠D,
∵AB∥CD,
∴∠1=∠C,∠2=∠D,
∴∠1=∠2,
∵∠1=∠A+∠AOC,∠2=∠B+∠BOD,
而OA=OB,
∴∠A=∠B,
∴∠AOC=∠BOD,
∴弧AC与弧BD是等弧
22.证明:过点O作OG⊥AB于点G,延长OG与⊙O交于H.
∵OC=OD,OG⊥CD于点G,
∴∠COG=∠DOG,
∴=.
又∵OG⊥AB于点G,
∴=,
∴﹣=﹣,
即=.
23.解:与相等,理由如下:
连接OA,OB,过点O作OE⊥PA于E,OF⊥PB于F.
∴点O在∠APB的平分线PN上,
∴OE=OF,
∵∠OEA=∠OFB=90°,
在Rt△OEA和Rt△OFB中,
,
∴Rt△OEA≌Rt△OFB(HL),
∴∠A=∠B,
∵∠AON=∠APO+∠A,∠BON=∠BPN+∠B
∴∠AON=∠BON,
∴∠AOM=∠BOM,
∴=.
