2021-2022学年北师大版九年级数学下册2-5二次函数与一元二次方程 同步自主提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2-5二次函数与一元二次方程 同步自主提升训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 20:45:01 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《2-5二次函数与一元二次方程》
同步自主提升训练(附答案)
1.对于二次函数y=(x﹣1)2﹣2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.与x轴有两个交点 D.顶点坐标是(﹣1,﹣2)
2.如图为某二次函数的部分图象,有如下四个结论:①此二次函数表达式为y=x2﹣x+9:②若点B(﹣1,n)在这个二次函数图象上,则n>m;③该二次函数图象与x轴的另一个交点为(﹣4,0);④当0<x<5.5时,m<y<8.所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
3.二次函数y= x2+mx+n的对称轴为x=﹣1,点(﹣5, y1),(﹣3, y2)在此函数的图象上,则有( )
A. y1>y2 B. y1=y2
C. y2>y1 D.以上均有可能
4.函数y=mx2+2x+1的图象与x轴只有1个公共点,则常数m的值是( )
A.1 B.2 C.0,1 D.1,2
5.抛物线y=﹣x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
A.x<﹣4或x>1 B.x<﹣3或x>1 C.﹣4<x<1 D.﹣3<x<1
6.如图是二次函数y1=ax2+bx+c和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是( )
A.﹣1<x<2 B.﹣1≤x≤2 C.x≤﹣1或x≥2 D.x<﹣1或x>2
7.设方程(x﹣1)(x﹣2)=30的两实根分别为α、β,且α<β,则α、β满足( )
A.1<α<β<2 B.1<α<2<β C.α<1<β<2 D.α<1<2<β
8.如图,抛物线y=x2+1与双曲线y=的交点A的横坐标是1,则关于x的不等式﹣1>0的解集是( )
A.x>1 B.x<﹣1 C.0<x<1 D.﹣1<x<0
9.如图所示是二次函数y=﹣x2+1的图象在x轴上方的一部分,对于这项图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
A.1 B. C. D.2
10.已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c﹣9=0的根的情况是( )
A.有两个不相等的正实数根 B.有两个异号实数根
C.有两个相等的实数根 D.没有实数根
11.若函数y=x2﹣2x+b的图象与坐标轴有三个交点,则b的取值范围是( )
A.b<1且b≠0 B.b>1 C.0<b<1 D.b<1
12.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解的范围是( )
x 6.17 6.18 6.19
y ﹣0.03 ﹣0.01 0.02
A.﹣0.03<x<﹣0.01 B.﹣0.01<x<0.02
C.6.18<x<6.19 D.6.17<x<6.18
13.如图,二次函数y=﹣x2+mx的图象与x轴交于坐标原点和(4,0),若关于x的方程x2﹣mx+t=0(t为实数)在1<x<4的范围内有解,则t的取值范围是 .
14.抛物线经过坐标系(﹣1,0)和(0,3)两点,对称轴x=1,如图所示,则当y<0时,x的取值范围是 .
15.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2﹣mx+c>n的解集是 .
16.二次函数y=x2﹣2x+m的图象与x轴只有一个公共点,则m的值为 .
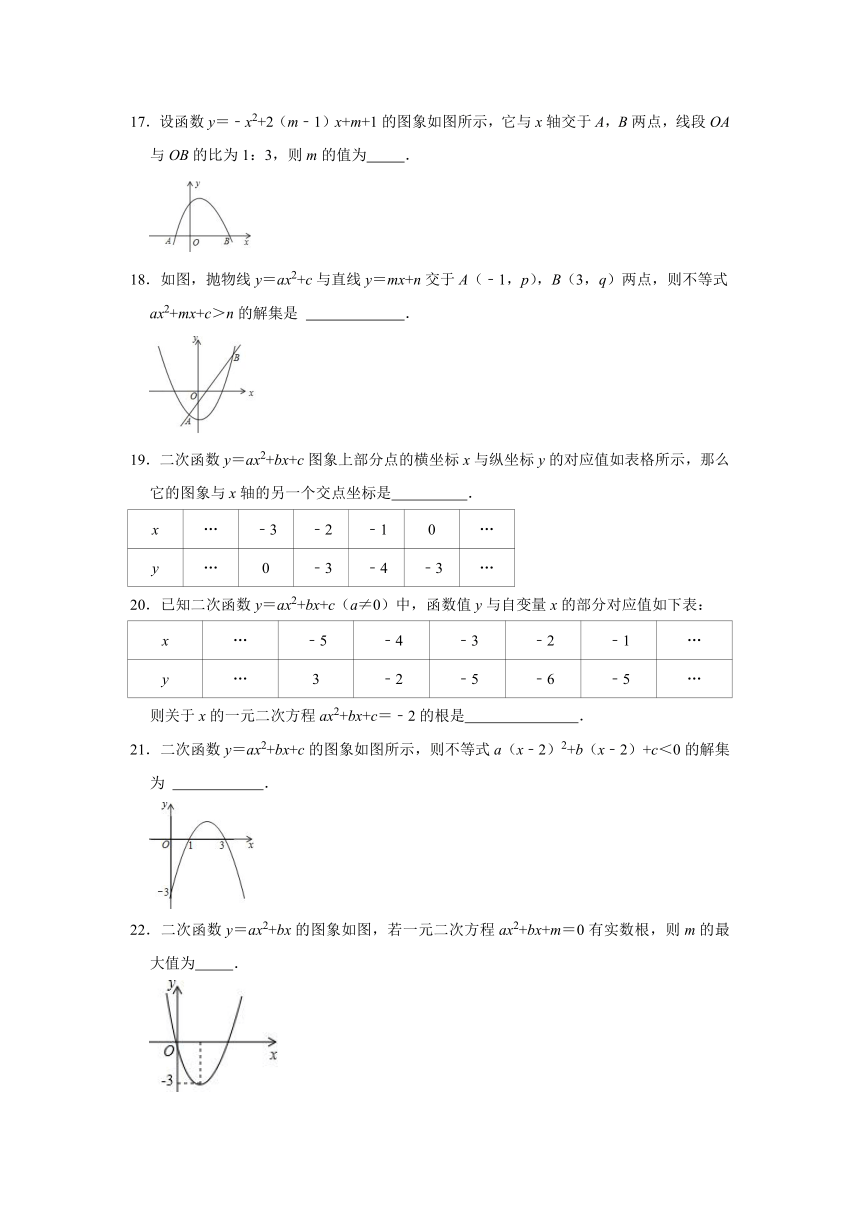
17.设函数y=﹣x2+2(m﹣1)x+m+1的图象如图所示,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为 .
18.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是 .
19.二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示,那么它的图象与x轴的另一个交点坐标是 .
x … ﹣3 ﹣2 ﹣1 0 …
y … 0 ﹣3 ﹣4 ﹣3 …
20.已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 …
y … 3 ﹣2 ﹣5 ﹣6 ﹣5 …
则关于x的一元二次方程ax2+bx+c=﹣2的根是 .
21.二次函数y=ax2+bx+c的图象如图所示,则不等式a(x﹣2)2+b(x﹣2)+c<0的解集为 .
22.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 .
23.已知关于x的二次函数y=ax2+(a2﹣1)x﹣a的图象与x轴的一个交点的坐标为(m,0),若<m<1,则a的取值范围是 .
24.二次函数y=x2﹣x+1的图象与x轴的交点个数是 .
25.若关于x的二次函数=ax2+2x﹣5的图象与x轴有两个交点,且其中有且仅有一个交点在原点和A(1,0)之间(不含原点和A点),则a的取值范围是 .
26.小红根据学习函数的经验,对函数y=|x(x﹣8)|的图象与性质进行了探究.下面是小红的探究过程,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
x … ﹣2 ﹣1 0 1 2 3 4 5 6 7 8 9 10 …
y … 20 9 0 7 12 15 m 15 12 7 0 9 20 …
其中m= ;
(2)如图,在平面直角坐标系xOy中,描出了以如表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察函数图象,写出一条该函数的性质 ;
(4)进一步探究函数图象发现:
①当x= 时|x(x﹣8)|的值为0;
②有两个点(x1,y1)和(x2,y2)在此函数图象上,当x2>x1>8时,比较y1和y2的大小关系为:y1 y2(填“>”、“<”或“=”);
③若关于x的方程|x(x﹣8)|=a有4个互不相等的解,则a的取值范围是 .
④当2≤x≤10时,y的取值范围是 .
27.已知二次函数y=x2﹣2mx+2m﹣1(m为常数).
(1)求证:不论m为何值,该函数图象与x轴一定有公共点;
(2)求证:不论m为何值,该函数图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)已知点A(a,﹣1),B(a+2,﹣1),线段AB与函数y=﹣(x﹣1)2的图象有公共点,则a的取值范围是 .
28.《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x﹣h)2﹣4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.
29.有这样一个问题:探究函数y=﹣x的图象与性质.
小东根据学习函数的经验,对函数y=﹣x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=﹣x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值,求m的值;
x … ﹣4 ﹣3 ﹣2 ﹣ ﹣1 ﹣ 1 2 3 4 …
y … ﹣ ﹣ m …
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第二象限内的最低点的坐标是(﹣2,),结合函数的图象,写出该函数的其它性质(一条即可) .
(5)根据函数图象估算方程﹣x=2的根为 .(精确到0.1)
30.已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点的坐标为A(﹣1,0),与y轴的交点的坐标为C(0,﹣3).
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点B的坐标;
(3)根据图象回答:当x取何值时,y<0;
(4)连接AC、BC,求△ABC的面积.
参考答案
1.解:根据抛物线的性质由a=1得到图象开口向上,根据顶点式得到顶点坐标为(1,﹣2),对称轴为直线x=1,故A,B,D错误,
令y=0,即(x﹣1)2﹣2x2﹣2x﹣1=0,
∵△=(﹣2)2﹣4×1×(﹣1)=8>0,
∴二次函数y=(x﹣1)2﹣2的图象与x轴有两个交点,
故C正确,
故选:C.
2.解:①由图象顶点(2,9)可得y=a(x﹣2)2+9,
将(8,0)代入y=a(x﹣2)2+9得0=36a+9,
解得a=﹣,
∴y=﹣(x﹣2)2+9=y=﹣x2+x+8,
故①错误.
②∵5.5﹣2>2﹣(﹣1),
点A距离对称轴距离大于点B距离对称轴距离,
∴m<n,
故②正确.
③∵图象对称轴为直线x=2,且抛物线与x轴一个交点为(8,0),
∴图象与x轴的另一交点横坐标为2×2﹣8=﹣4,
故③正确.
④由图象可得当x=0时y=8,x=5.5时y=m,x=2时y=9,
∴0<x<5.5时,m<y≤9.
故④错误.
故选:C.
3.解:∵二次函数y=x2+mx+n的对称轴为x=﹣1,
∴当x>﹣1时,y随x的增大而增大,当x<﹣1时,y随x的增大而减小,
∵点(﹣5,y1)(﹣3,y2)在此函数的图象上,
∴y1>y2,
故选:A.
4.解:①若m=0,则函数y=2x+1,是一次函数,与x轴只有一个交点;
②若m≠0,则函数y=mx2+2x+1,是二次函数.
根据题意得:△=4﹣4m=0,
解得:m=1.
故m为0或1.
故选:C.
5.解:函数的对称轴为:x=﹣1,与x轴的一个交点坐标为(1,0),
则另外一个交点坐标为:(﹣3,0),
故:y<0时,x<﹣3或x>1,
故选:B.
6.解:从图象可以看出,﹣1≤x≤2时,抛物线的函数值大于一次函数的值,
故选:B.
7.解:方程(x﹣1)(x﹣2)=30,
整理,得x2﹣3x﹣28=0
解得x1=﹣4,x2=7
因为方程的两实根分别为α、β,且α<β,
所以α=﹣4,β=7
所以α<1<2<β.
故选:D.
8.解:由﹣x2﹣1<0得,x2+1<,
∵点A的横坐标为1,如图所示,
∴不等式的解集是0<x<1.
故选:C.
9.解:∵二次函数y=﹣x2+1,
当x=0时,y=1,
当y=0时,﹣x2+1=0,
∴x=±1,
∴二次函数y=﹣x2+1的图象与坐标轴的简单坐标为:(0,1),(1,0),(﹣1,0),
∴这三个交点围成的三角形的面积为:×1×2=1,
而所求面积大于这个三角形的面积,
∴图象与x轴所围成的阴影部分的面积与其最接近的值为,
故选:B.
10.解:∵y=ax2+bx+c的图象顶点纵坐标为8,向下平移9个单位即可得到y=ax2+bx+c﹣9的图象,
此时,抛物线与x轴无点,
∴方程ax2+bx+c﹣9=0无实数根.
故选:D.
11.解:∵函数y=x2﹣2x+b的图象与坐标轴有三个交点,如果b=0,那么此二次函数与两坐标轴的其中一个交点重合了,那么就只有2个交点,则于题意不符,
∴,
解得b<1且b≠0.
故选:A.
12.解:由表格中的数据看出﹣0.01和0.02更接近于0,
故x应取对应的范围为:6.18<x<6.19,
故选:C.
13.解:∵抛物线的对称轴为直线x=,解得m=4,
∴抛物线解析式为y=﹣x2+4x,
抛物线的顶点坐标为(2,4),
当x=1时,y=﹣x2+4x=﹣1+4=3;
当x=4时,y=﹣x2+4x=﹣16+16=0,
当x=2时,y=4,
在1<x<4时有公共点时
当直线y=t与抛物线y=﹣x2+4x在1<x<4时有公共点时,0<t≤4,
故答案为0<t≤4.
14.解:∵函数的对称轴为x=1,抛物线和x轴的一个交点为(﹣1,0),
∴抛物线和x轴的另外一个交点坐标为(3,0),
则根据函数图象,当y<0时,x的取值范围是x<﹣1或x>3,
故答案为:x<﹣1或x>3.
15.解:∵抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,
∴ax2+c>mx+n的解集是x<﹣1或x>3,
∴ax2﹣mx+c>n的解集是x<﹣1或x>3,
故答案为:x<﹣1或x>3.
16.解:根据题意得△=(﹣2)2﹣4m=0,
解得m=1.
故答案为1.
17.解:设点A的坐标为(﹣a,0),点B的坐标为(3a,0).
由根与系数的关系可知:﹣a+3a=2(m﹣1),﹣a 3a=﹣(m+1),
整理得:a=m﹣1,3a2=m+1
将a=m﹣1代入得:3(m﹣1)2=m+1.
解得:m=2或m=(舍去).
故答案为:2.
18.解:∵直线y=mx+n与直线y=﹣mx+n关于y轴对称,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,
∴抛物线y=ax2+c与直线y=﹣mx+n交于(1,p),(﹣3,q)两点,
观察函数图象可知:当x<﹣3或x>1时,直线y=﹣mx+n在抛物线y=ax2+c的下方,
∴不等式ax2+c>﹣mx+n的解集为x<﹣3或x>1,
即不等式ax2+mx+c>n的解集是x<﹣3或x>1.
故答案为:x<﹣3或x>1.
19.解:∵x=﹣2,y=﹣3;x=0时,y=﹣3,
∴抛物线的对称轴为直线x=﹣1,
∵抛物线与x轴的一个交点坐标为(﹣3,0),
∴抛物线与x轴的一个交点坐标为(1,0).
故答案为(1,0).
20.解:∵x=﹣3,x=﹣1的函数值都是﹣5,相等,
∴二次函数的对称轴为直线x=﹣2,
∵x=﹣4时,y=﹣2,
∴x=0时,y=﹣2,
∴方程ax2+bx+c=﹣2的解是x1=﹣4,x2=0.
故答案为:x1=﹣4,x2=0.
21.解:∵由函数图象可知,当x=1,3时,y=0,
令t=x﹣2,
∴a(x﹣2)2+b(x﹣2)+c=at2+bt+c=0的解为:
t=1或3,
解得x=3或5,
∴不等式a(x﹣2)2+b(x﹣2)+c<0的解集为x<3或x>5.
故答案为:x<3或x>5.
22.方法一解:∵抛物线的开口向上,顶点纵坐标为﹣3,
∴a>0.
﹣=﹣3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2﹣4am≥0,即12a﹣4am≥0,即12﹣4m≥0,解得m≤3,
∴m的最大值为3,
方法二:解:一元二次方程ax2+bx+m=0有实数根,则二次函数y=ax2+bx的图象与直线y=﹣m有交点,
由图象得,﹣m≥﹣3,解得m≤3,
∴m的最大值为3,
故答案为3.
23.解:∵y=ax2+(a2﹣1)x﹣a=(ax﹣1)(x+a),
∴当y=0时,x1=,x2=﹣a,
∴抛物线与x轴的交点为(,0)和(﹣a,0).
∵抛物线与x轴的一个交点的坐标为(m,0)且<m<1,
∴当a>0时,<<1,解得1<a<2;
当a<0时,<﹣a<1,解得﹣1<a<﹣.
故答案为:1<a<2或﹣1<a<﹣.
24.解:∵Δ=b2﹣4ac=1﹣4=﹣3<0,
∴抛物线与x轴没有交点,
∴交点个数为O.
故答案为0.
25.解:∵关于x的二次函数y=ax2+2x﹣5的图象与x轴有两个交点,
∴△=4+20a>0,
解得a>﹣.①
又∵有一个交点的横坐标在0和1之间(不含0和1),
∴当x=0时,y<0.
当x=1时,y>0,
即a﹣3>0,
解得a>3.②
结合①②得到:a>3.
故答案为:a>3.
26.解:(1)将x=4,代入到y=|x(x﹣8)|中,
得:y=|4×(4﹣8)|=16,
∴m=16,
故答案为:16;
(2)如图:
(3)当x>8时,y随x的增大而增大(答案不唯一);
(4)①|x(x﹣8)|=0,
x=0或8,
故答案为:0或8;
②当x>8时,y随x的增大而增大,
∴y1<y2,
故答案为:<;
③|x(x﹣8)|=a有4个解,则a>0,
∴方程可变为:x(x﹣8)=a和x(x﹣8)=﹣a,
这两个方程均有两个不相等的实数根,
有82+4a>0,82﹣4a>0,
解得:0<a<16,
故答案为:0<a<16;
④y=|x(x﹣8)|=|(x﹣4)2﹣16|,
∵2≤x≤10,
此时(x﹣4)2﹣16的最小值为﹣12,最大值为20,
所以y=|x(x﹣8)|的最小值为0,最大值为20,
即0≤y≤20,
故答案为:0≤y≤20.
27.(1)证明:∵△=4m2﹣4(2m﹣1)
=4m2﹣8m+4
=4(m﹣1)2≥0,
所以不论m为何值,该二次函数的图象与x轴总有公共点;
(2)证明:y=x2﹣2mx+2m﹣1=(x﹣m)2﹣(m﹣1)2,
二次函数y=x2﹣2mx+2m﹣1的顶点坐标为(m,﹣(m﹣1)2)
当x=m时,y=﹣(x﹣1)2=﹣(m﹣1)2,
所以不论m为何值,该二次函数的图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)当y=﹣1时,y=﹣(x﹣1)2=﹣1,解得x1=0,x2=2,
当a+2≥0且a≤2时,线段AB与函数y=﹣(x﹣1)2的图象有公共点,
所以a的范围为﹣2≤a≤2.
故答案为﹣2≤a≤2.
28.解:【问题】
将点(0,0)代入y=a(x﹣2)2﹣4,得:4a﹣4=0,
解得a=1,
则抛物线解析式为y=(x﹣2)2﹣4,
令y=0得(x﹣2)2﹣4=0,
解得x1=0、x2=4,
∴点A坐标为(4,0),
故答案为:1、(4,0);
【操作】
因为翻折后抛物线与原抛物线开口方向相反、形状相同,且新抛物的顶点坐标为(2,4),
所以翻折后的这部分抛物线对应的函数解析式y=﹣(x﹣2)2+4,
故答案为:y=﹣(x﹣2)2+4;
【探究】
在图2中,新图象对应的函数y随x的增大而增大时,x的取值范围是0<x<2或x>4,
故答案为:0<x<2或x>4;
【应用】
(1)令y=0得(x﹣h)2﹣4=0,
解得:x1=h+2、x2=h﹣2,
∴点A(h﹣2,0)B(h+2,0);
(2)∵当1<x<2时,新图象的函数值y随x的增大而增大,
∴h﹣2≤1且2≤h或h+2≤1,
解得:2≤h≤3或h≤﹣1.
29.解:(1)函数y=﹣x的自变量x的取值范围是:x≠0,
故答案为:x≠0;
(2)把x=4代入y=﹣x得,y=﹣×4=﹣,
∴m=﹣,
(3)如图所示
,
(4)当x>0时,y随x的增大而减小;
故答案为当x>0时,y随x的增大而减小;
(5)由图象,得
x1=0.8,x2=﹣1.2,x3=﹣3.9.
故答案为:x1=0.8,x2=﹣1.2,x3=﹣3.9.
30.解:(1)由二次函数y=x2+bx+c的图象经过(﹣1,0)和(0,﹣3)两点,
得,
解得.
则抛物线的解析式为y=x2﹣2x﹣3;
(2)由(1)知,抛物线的解析式为y=x2﹣2x﹣3,或y=(x﹣3)(x+1),
则该抛物线与x轴的交点坐标是:A(﹣1,0),B(3,0);
(3)根据图象知,当﹣1<x<3时,y<0;
(4)∵A(﹣1,0),B(3,0),C(0,﹣3),
∴AB=4,OC=3,
∴△ABC的面积是:AB OC=×4×3=6.
同步自主提升训练(附答案)
1.对于二次函数y=(x﹣1)2﹣2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=﹣1
C.与x轴有两个交点 D.顶点坐标是(﹣1,﹣2)
2.如图为某二次函数的部分图象,有如下四个结论:①此二次函数表达式为y=x2﹣x+9:②若点B(﹣1,n)在这个二次函数图象上,则n>m;③该二次函数图象与x轴的另一个交点为(﹣4,0);④当0<x<5.5时,m<y<8.所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
3.二次函数y= x2+mx+n的对称轴为x=﹣1,点(﹣5, y1),(﹣3, y2)在此函数的图象上,则有( )
A. y1>y2 B. y1=y2
C. y2>y1 D.以上均有可能
4.函数y=mx2+2x+1的图象与x轴只有1个公共点,则常数m的值是( )
A.1 B.2 C.0,1 D.1,2
5.抛物线y=﹣x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
A.x<﹣4或x>1 B.x<﹣3或x>1 C.﹣4<x<1 D.﹣3<x<1
6.如图是二次函数y1=ax2+bx+c和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是( )
A.﹣1<x<2 B.﹣1≤x≤2 C.x≤﹣1或x≥2 D.x<﹣1或x>2
7.设方程(x﹣1)(x﹣2)=30的两实根分别为α、β,且α<β,则α、β满足( )
A.1<α<β<2 B.1<α<2<β C.α<1<β<2 D.α<1<2<β
8.如图,抛物线y=x2+1与双曲线y=的交点A的横坐标是1,则关于x的不等式﹣1>0的解集是( )
A.x>1 B.x<﹣1 C.0<x<1 D.﹣1<x<0
9.如图所示是二次函数y=﹣x2+1的图象在x轴上方的一部分,对于这项图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
A.1 B. C. D.2
10.已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c﹣9=0的根的情况是( )
A.有两个不相等的正实数根 B.有两个异号实数根
C.有两个相等的实数根 D.没有实数根
11.若函数y=x2﹣2x+b的图象与坐标轴有三个交点,则b的取值范围是( )
A.b<1且b≠0 B.b>1 C.0<b<1 D.b<1
12.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解的范围是( )
x 6.17 6.18 6.19
y ﹣0.03 ﹣0.01 0.02
A.﹣0.03<x<﹣0.01 B.﹣0.01<x<0.02
C.6.18<x<6.19 D.6.17<x<6.18
13.如图,二次函数y=﹣x2+mx的图象与x轴交于坐标原点和(4,0),若关于x的方程x2﹣mx+t=0(t为实数)在1<x<4的范围内有解,则t的取值范围是 .
14.抛物线经过坐标系(﹣1,0)和(0,3)两点,对称轴x=1,如图所示,则当y<0时,x的取值范围是 .
15.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2﹣mx+c>n的解集是 .
16.二次函数y=x2﹣2x+m的图象与x轴只有一个公共点,则m的值为 .
17.设函数y=﹣x2+2(m﹣1)x+m+1的图象如图所示,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为 .
18.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是 .
19.二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示,那么它的图象与x轴的另一个交点坐标是 .
x … ﹣3 ﹣2 ﹣1 0 …
y … 0 ﹣3 ﹣4 ﹣3 …
20.已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 …
y … 3 ﹣2 ﹣5 ﹣6 ﹣5 …
则关于x的一元二次方程ax2+bx+c=﹣2的根是 .
21.二次函数y=ax2+bx+c的图象如图所示,则不等式a(x﹣2)2+b(x﹣2)+c<0的解集为 .
22.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 .
23.已知关于x的二次函数y=ax2+(a2﹣1)x﹣a的图象与x轴的一个交点的坐标为(m,0),若<m<1,则a的取值范围是 .
24.二次函数y=x2﹣x+1的图象与x轴的交点个数是 .
25.若关于x的二次函数=ax2+2x﹣5的图象与x轴有两个交点,且其中有且仅有一个交点在原点和A(1,0)之间(不含原点和A点),则a的取值范围是 .
26.小红根据学习函数的经验,对函数y=|x(x﹣8)|的图象与性质进行了探究.下面是小红的探究过程,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
x … ﹣2 ﹣1 0 1 2 3 4 5 6 7 8 9 10 …
y … 20 9 0 7 12 15 m 15 12 7 0 9 20 …
其中m= ;
(2)如图,在平面直角坐标系xOy中,描出了以如表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察函数图象,写出一条该函数的性质 ;
(4)进一步探究函数图象发现:
①当x= 时|x(x﹣8)|的值为0;
②有两个点(x1,y1)和(x2,y2)在此函数图象上,当x2>x1>8时,比较y1和y2的大小关系为:y1 y2(填“>”、“<”或“=”);
③若关于x的方程|x(x﹣8)|=a有4个互不相等的解,则a的取值范围是 .
④当2≤x≤10时,y的取值范围是 .
27.已知二次函数y=x2﹣2mx+2m﹣1(m为常数).
(1)求证:不论m为何值,该函数图象与x轴一定有公共点;
(2)求证:不论m为何值,该函数图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)已知点A(a,﹣1),B(a+2,﹣1),线段AB与函数y=﹣(x﹣1)2的图象有公共点,则a的取值范围是 .
28.《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x﹣h)2﹣4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.
29.有这样一个问题:探究函数y=﹣x的图象与性质.
小东根据学习函数的经验,对函数y=﹣x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=﹣x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值,求m的值;
x … ﹣4 ﹣3 ﹣2 ﹣ ﹣1 ﹣ 1 2 3 4 …
y … ﹣ ﹣ m …
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第二象限内的最低点的坐标是(﹣2,),结合函数的图象,写出该函数的其它性质(一条即可) .
(5)根据函数图象估算方程﹣x=2的根为 .(精确到0.1)
30.已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点的坐标为A(﹣1,0),与y轴的交点的坐标为C(0,﹣3).
(1)求此二次函数的解析式;
(2)求此二次函数的图象与x轴的另一个交点B的坐标;
(3)根据图象回答:当x取何值时,y<0;
(4)连接AC、BC,求△ABC的面积.
参考答案
1.解:根据抛物线的性质由a=1得到图象开口向上,根据顶点式得到顶点坐标为(1,﹣2),对称轴为直线x=1,故A,B,D错误,
令y=0,即(x﹣1)2﹣2x2﹣2x﹣1=0,
∵△=(﹣2)2﹣4×1×(﹣1)=8>0,
∴二次函数y=(x﹣1)2﹣2的图象与x轴有两个交点,
故C正确,
故选:C.
2.解:①由图象顶点(2,9)可得y=a(x﹣2)2+9,
将(8,0)代入y=a(x﹣2)2+9得0=36a+9,
解得a=﹣,
∴y=﹣(x﹣2)2+9=y=﹣x2+x+8,
故①错误.
②∵5.5﹣2>2﹣(﹣1),
点A距离对称轴距离大于点B距离对称轴距离,
∴m<n,
故②正确.
③∵图象对称轴为直线x=2,且抛物线与x轴一个交点为(8,0),
∴图象与x轴的另一交点横坐标为2×2﹣8=﹣4,
故③正确.
④由图象可得当x=0时y=8,x=5.5时y=m,x=2时y=9,
∴0<x<5.5时,m<y≤9.
故④错误.
故选:C.
3.解:∵二次函数y=x2+mx+n的对称轴为x=﹣1,
∴当x>﹣1时,y随x的增大而增大,当x<﹣1时,y随x的增大而减小,
∵点(﹣5,y1)(﹣3,y2)在此函数的图象上,
∴y1>y2,
故选:A.
4.解:①若m=0,则函数y=2x+1,是一次函数,与x轴只有一个交点;
②若m≠0,则函数y=mx2+2x+1,是二次函数.
根据题意得:△=4﹣4m=0,
解得:m=1.
故m为0或1.
故选:C.
5.解:函数的对称轴为:x=﹣1,与x轴的一个交点坐标为(1,0),
则另外一个交点坐标为:(﹣3,0),
故:y<0时,x<﹣3或x>1,
故选:B.
6.解:从图象可以看出,﹣1≤x≤2时,抛物线的函数值大于一次函数的值,
故选:B.
7.解:方程(x﹣1)(x﹣2)=30,
整理,得x2﹣3x﹣28=0
解得x1=﹣4,x2=7
因为方程的两实根分别为α、β,且α<β,
所以α=﹣4,β=7
所以α<1<2<β.
故选:D.
8.解:由﹣x2﹣1<0得,x2+1<,
∵点A的横坐标为1,如图所示,
∴不等式的解集是0<x<1.
故选:C.
9.解:∵二次函数y=﹣x2+1,
当x=0时,y=1,
当y=0时,﹣x2+1=0,
∴x=±1,
∴二次函数y=﹣x2+1的图象与坐标轴的简单坐标为:(0,1),(1,0),(﹣1,0),
∴这三个交点围成的三角形的面积为:×1×2=1,
而所求面积大于这个三角形的面积,
∴图象与x轴所围成的阴影部分的面积与其最接近的值为,
故选:B.
10.解:∵y=ax2+bx+c的图象顶点纵坐标为8,向下平移9个单位即可得到y=ax2+bx+c﹣9的图象,
此时,抛物线与x轴无点,
∴方程ax2+bx+c﹣9=0无实数根.
故选:D.
11.解:∵函数y=x2﹣2x+b的图象与坐标轴有三个交点,如果b=0,那么此二次函数与两坐标轴的其中一个交点重合了,那么就只有2个交点,则于题意不符,
∴,
解得b<1且b≠0.
故选:A.
12.解:由表格中的数据看出﹣0.01和0.02更接近于0,
故x应取对应的范围为:6.18<x<6.19,
故选:C.
13.解:∵抛物线的对称轴为直线x=,解得m=4,
∴抛物线解析式为y=﹣x2+4x,
抛物线的顶点坐标为(2,4),
当x=1时,y=﹣x2+4x=﹣1+4=3;
当x=4时,y=﹣x2+4x=﹣16+16=0,
当x=2时,y=4,
在1<x<4时有公共点时
当直线y=t与抛物线y=﹣x2+4x在1<x<4时有公共点时,0<t≤4,
故答案为0<t≤4.
14.解:∵函数的对称轴为x=1,抛物线和x轴的一个交点为(﹣1,0),
∴抛物线和x轴的另外一个交点坐标为(3,0),
则根据函数图象,当y<0时,x的取值范围是x<﹣1或x>3,
故答案为:x<﹣1或x>3.
15.解:∵抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,
∴ax2+c>mx+n的解集是x<﹣1或x>3,
∴ax2﹣mx+c>n的解集是x<﹣1或x>3,
故答案为:x<﹣1或x>3.
16.解:根据题意得△=(﹣2)2﹣4m=0,
解得m=1.
故答案为1.
17.解:设点A的坐标为(﹣a,0),点B的坐标为(3a,0).
由根与系数的关系可知:﹣a+3a=2(m﹣1),﹣a 3a=﹣(m+1),
整理得:a=m﹣1,3a2=m+1
将a=m﹣1代入得:3(m﹣1)2=m+1.
解得:m=2或m=(舍去).
故答案为:2.
18.解:∵直线y=mx+n与直线y=﹣mx+n关于y轴对称,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,
∴抛物线y=ax2+c与直线y=﹣mx+n交于(1,p),(﹣3,q)两点,
观察函数图象可知:当x<﹣3或x>1时,直线y=﹣mx+n在抛物线y=ax2+c的下方,
∴不等式ax2+c>﹣mx+n的解集为x<﹣3或x>1,
即不等式ax2+mx+c>n的解集是x<﹣3或x>1.
故答案为:x<﹣3或x>1.
19.解:∵x=﹣2,y=﹣3;x=0时,y=﹣3,
∴抛物线的对称轴为直线x=﹣1,
∵抛物线与x轴的一个交点坐标为(﹣3,0),
∴抛物线与x轴的一个交点坐标为(1,0).
故答案为(1,0).
20.解:∵x=﹣3,x=﹣1的函数值都是﹣5,相等,
∴二次函数的对称轴为直线x=﹣2,
∵x=﹣4时,y=﹣2,
∴x=0时,y=﹣2,
∴方程ax2+bx+c=﹣2的解是x1=﹣4,x2=0.
故答案为:x1=﹣4,x2=0.
21.解:∵由函数图象可知,当x=1,3时,y=0,
令t=x﹣2,
∴a(x﹣2)2+b(x﹣2)+c=at2+bt+c=0的解为:
t=1或3,
解得x=3或5,
∴不等式a(x﹣2)2+b(x﹣2)+c<0的解集为x<3或x>5.
故答案为:x<3或x>5.
22.方法一解:∵抛物线的开口向上,顶点纵坐标为﹣3,
∴a>0.
﹣=﹣3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2﹣4am≥0,即12a﹣4am≥0,即12﹣4m≥0,解得m≤3,
∴m的最大值为3,
方法二:解:一元二次方程ax2+bx+m=0有实数根,则二次函数y=ax2+bx的图象与直线y=﹣m有交点,
由图象得,﹣m≥﹣3,解得m≤3,
∴m的最大值为3,
故答案为3.
23.解:∵y=ax2+(a2﹣1)x﹣a=(ax﹣1)(x+a),
∴当y=0时,x1=,x2=﹣a,
∴抛物线与x轴的交点为(,0)和(﹣a,0).
∵抛物线与x轴的一个交点的坐标为(m,0)且<m<1,
∴当a>0时,<<1,解得1<a<2;
当a<0时,<﹣a<1,解得﹣1<a<﹣.
故答案为:1<a<2或﹣1<a<﹣.
24.解:∵Δ=b2﹣4ac=1﹣4=﹣3<0,
∴抛物线与x轴没有交点,
∴交点个数为O.
故答案为0.
25.解:∵关于x的二次函数y=ax2+2x﹣5的图象与x轴有两个交点,
∴△=4+20a>0,
解得a>﹣.①
又∵有一个交点的横坐标在0和1之间(不含0和1),
∴当x=0时,y<0.
当x=1时,y>0,
即a﹣3>0,
解得a>3.②
结合①②得到:a>3.
故答案为:a>3.
26.解:(1)将x=4,代入到y=|x(x﹣8)|中,
得:y=|4×(4﹣8)|=16,
∴m=16,
故答案为:16;
(2)如图:
(3)当x>8时,y随x的增大而增大(答案不唯一);
(4)①|x(x﹣8)|=0,
x=0或8,
故答案为:0或8;
②当x>8时,y随x的增大而增大,
∴y1<y2,
故答案为:<;
③|x(x﹣8)|=a有4个解,则a>0,
∴方程可变为:x(x﹣8)=a和x(x﹣8)=﹣a,
这两个方程均有两个不相等的实数根,
有82+4a>0,82﹣4a>0,
解得:0<a<16,
故答案为:0<a<16;
④y=|x(x﹣8)|=|(x﹣4)2﹣16|,
∵2≤x≤10,
此时(x﹣4)2﹣16的最小值为﹣12,最大值为20,
所以y=|x(x﹣8)|的最小值为0,最大值为20,
即0≤y≤20,
故答案为:0≤y≤20.
27.(1)证明:∵△=4m2﹣4(2m﹣1)
=4m2﹣8m+4
=4(m﹣1)2≥0,
所以不论m为何值,该二次函数的图象与x轴总有公共点;
(2)证明:y=x2﹣2mx+2m﹣1=(x﹣m)2﹣(m﹣1)2,
二次函数y=x2﹣2mx+2m﹣1的顶点坐标为(m,﹣(m﹣1)2)
当x=m时,y=﹣(x﹣1)2=﹣(m﹣1)2,
所以不论m为何值,该二次函数的图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)当y=﹣1时,y=﹣(x﹣1)2=﹣1,解得x1=0,x2=2,
当a+2≥0且a≤2时,线段AB与函数y=﹣(x﹣1)2的图象有公共点,
所以a的范围为﹣2≤a≤2.
故答案为﹣2≤a≤2.
28.解:【问题】
将点(0,0)代入y=a(x﹣2)2﹣4,得:4a﹣4=0,
解得a=1,
则抛物线解析式为y=(x﹣2)2﹣4,
令y=0得(x﹣2)2﹣4=0,
解得x1=0、x2=4,
∴点A坐标为(4,0),
故答案为:1、(4,0);
【操作】
因为翻折后抛物线与原抛物线开口方向相反、形状相同,且新抛物的顶点坐标为(2,4),
所以翻折后的这部分抛物线对应的函数解析式y=﹣(x﹣2)2+4,
故答案为:y=﹣(x﹣2)2+4;
【探究】
在图2中,新图象对应的函数y随x的增大而增大时,x的取值范围是0<x<2或x>4,
故答案为:0<x<2或x>4;
【应用】
(1)令y=0得(x﹣h)2﹣4=0,
解得:x1=h+2、x2=h﹣2,
∴点A(h﹣2,0)B(h+2,0);
(2)∵当1<x<2时,新图象的函数值y随x的增大而增大,
∴h﹣2≤1且2≤h或h+2≤1,
解得:2≤h≤3或h≤﹣1.
29.解:(1)函数y=﹣x的自变量x的取值范围是:x≠0,
故答案为:x≠0;
(2)把x=4代入y=﹣x得,y=﹣×4=﹣,
∴m=﹣,
(3)如图所示
,
(4)当x>0时,y随x的增大而减小;
故答案为当x>0时,y随x的增大而减小;
(5)由图象,得
x1=0.8,x2=﹣1.2,x3=﹣3.9.
故答案为:x1=0.8,x2=﹣1.2,x3=﹣3.9.
30.解:(1)由二次函数y=x2+bx+c的图象经过(﹣1,0)和(0,﹣3)两点,
得,
解得.
则抛物线的解析式为y=x2﹣2x﹣3;
(2)由(1)知,抛物线的解析式为y=x2﹣2x﹣3,或y=(x﹣3)(x+1),
则该抛物线与x轴的交点坐标是:A(﹣1,0),B(3,0);
(3)根据图象知,当﹣1<x<3时,y<0;
(4)∵A(﹣1,0),B(3,0),C(0,﹣3),
∴AB=4,OC=3,
∴△ABC的面积是:AB OC=×4×3=6.
