2021-2022学年人教版七年级数学下册5.1相交线寒假预习同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.1相交线寒假预习同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 106.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 21:32:04 | ||
图片预览




文档简介
2021-2022学年人教版七年级数学下册《5-1相交线》寒假预习同步练习(附答案)
1.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1) B.n2﹣n+1 C. D.
2.如图两条非平行的直线AB,CD被第三条直线EF所截,交点为PQ,那么这3条直线将所在平面分成( )
A.5个部分 B.6个部分 C.7个部分 D.8个部分
3.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.4 B.5 C.6 D.以上都不对
4.如图所示,∠1和∠2是对顶角的图形是( )
A.B.C.D.
5.如图,AB⊥CD,垂足为O,直线EF经过点O,若∠1=50°,则∠2=( )
A.30° B.40° C.50° D.60°
6.如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( )
A.①② B.①③ C.②③ D.①②③
7.如图,点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是( )
A.PA B.PC C.PB D.PD
8.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm B.5cm C.小于2cm D.不大于2cm
9.下列图中,∠1与∠2是同位角的是( )
A.B. C.D.
10.如图,直线l与∠BAC的两边分别相交于点D、E,则图中是同旁内角的有( )
A.2对 B.3对 C.4对 D.5对
11.四条直线两两相交,至多会有 个交点.
12.三条直线两两相交,则交点有 个.
13.平面内两直线相交有 个交点,两平面相交形成 条直线.
14.如图是一把剪刀,若∠AOB+∠COD=80°,则∠AOC= 度.
15.如图,已知AO⊥BC于O,∠BOD=120°,那么∠AOD= °.
16.如图,CD⊥AB于点D,∠EDF=90°,那么图中互补的角有 对.
17.如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.理由是 .
18.如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
19.如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=26°,求∠AOE和∠COE的度数.
20.已知,直线AB与直线CD相交于点O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(0<x<90),求∠AOE的度数.(用含x的代数式表示)
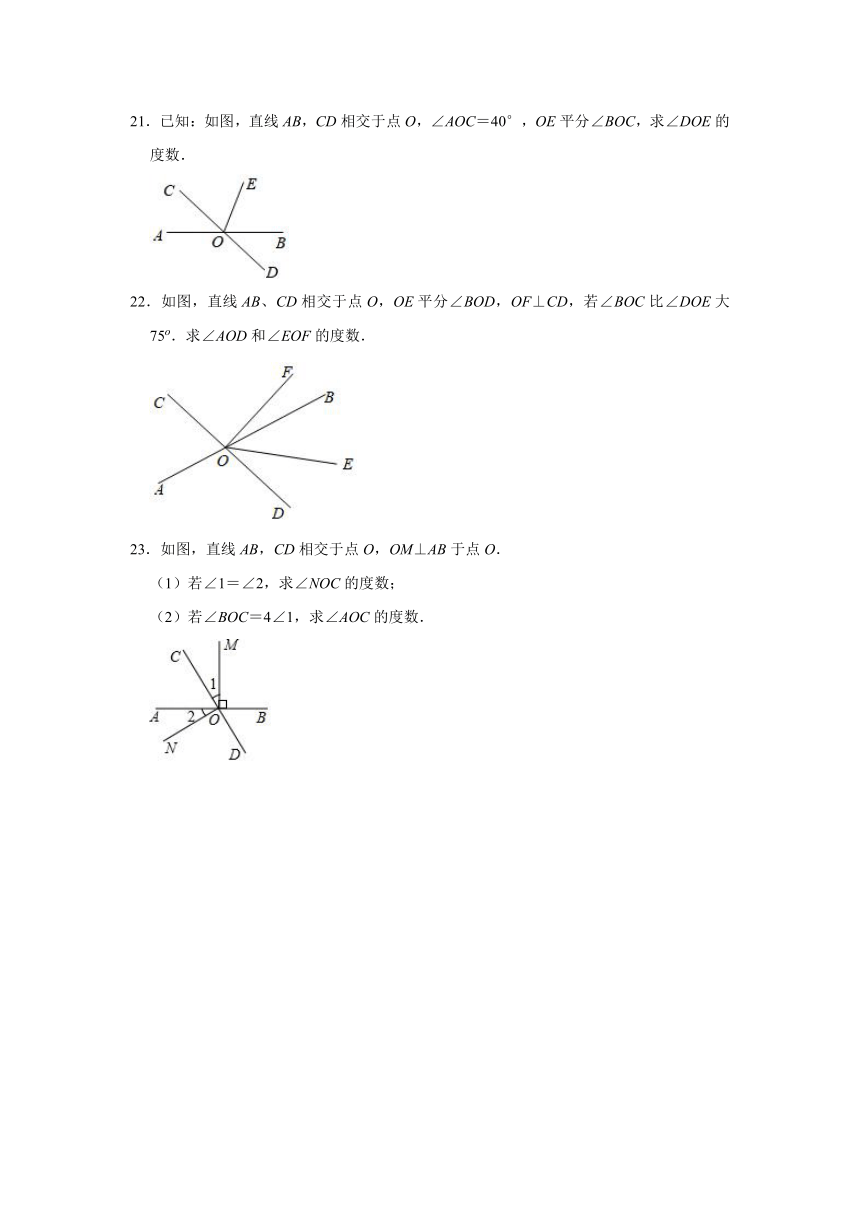
21.已知:如图,直线AB,CD相交于点O,∠AOC=40°,OE平分∠BOC,求∠DOE的度数.
22.如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,若∠BOC比∠DOE大75o.求∠AOD和∠EOF的度数.
23.如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOC的度数;
(2)若∠BOC=4∠1,求∠AOC的度数.
参考答案
1.解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;…
n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.
所以a=,而b=1,
∴a+b=.
故选:D.
2.解:因为直线是向两方无限延伸的所以应是7部分;
故选:C.
3.解:根据题意可得:3条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,3条直线相交,交点最多为3个,即n=3;
则m+n=1+3=4.
故选:A.
4.解:根据对顶角的意义,一个角的两条边分别是另一个角两边的反向延长线,这两个角是对顶角,
只有图B中的∠1和∠2是对顶角,
故选:B.
5.解:∵AB⊥CD,
∴∠BOD=90°,
∵∠BOD+∠1+∠2=180°,∠1=50°,
∴∠2=180°﹣∠BOD﹣∠1=180°﹣90°﹣50°=40°.
故选:B.
6.解:∵OE⊥CD于O,∠EOF=α,
∴∠DOF=α﹣90°,
∵OD平分∠BOF,
∴∠BOD=∠FOD,
∵∠AOC=∠BOD,
∴∠AOC=∠FOD,
∴∠AOC=α﹣90°,①正确;
∴∠BOE=180°﹣∠COE﹣∠AOC=180°﹣90°﹣(α﹣90°)=180°﹣α,②正确;
∴∠AOF=180°﹣∠AOC﹣∠DOF=180°﹣(α﹣90°)﹣(α﹣90°)=360°﹣2α,③正确;
故选:D.
7.解:由题意,得
点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是PB,
故选:C.
8.解:当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,
当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,
综上所述:点P到直线m的距离不大于2cm,
故选:D.
9.解:选项A中的两个角是同旁内角,因此不符合题意;
选项C中的两个角既不是同位角、也不是内错角、同旁内角,因此不符合题意;
选项D不是两条直线被一条直线所截出现的角,不符合题意;
只有选项B中的两个角符合同位角的意义,符合题意;
故选:B.
10.解:直线AC与直线AB被直线l所截形成的同旁内角有:∠ADE与∠AED、∠CDE与∠BED;
直线AC与直线DE被直线AB所截形成的同旁内角有:∠DAE与∠DEA;
直线AB与直线DE被直线AC所截形成的同旁内角有:∠EAD与∠EDA;
故选:C.
11.解:如图,可看出四条直线两两相交,至多有6个交点.
故填:6.
12.解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
13.解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
14.解:∵∠AOB+∠COD=80°,∠AOB=∠COD,
∴∠AOB=∠COD=40°,
又∵∠AOC+∠COD=180°,
∴∠AOC=180°﹣40°=140°,
故答案为:140.
15.解:∵AO⊥BC,
∴∠AOB=90°,
∵∠BOD=120°,
∴∠AOD=∠BOD﹣∠AOB=120°﹣90°=30°,
故答案是:30.
16.解:∠FDC与∠ADE是互补的角,∠CDE与∠FDB是互补的角,∠EDB与∠ADE是互补的角,∠ADC与∠CDB是互补的角,∠FDE与∠CDB是互补的角,∠FDE与∠ADC,∠ADF与∠BDF是互补的角.
故答案为:7.
17.解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
18.解:因为∠C=90°,
所以AC⊥BC,
所以A到BC的距离是AC,
因为线段AC=9cm,
所以点A到BC的距离为9cm.
故答案为:9.
19.解:∵∠AOC=26°,
∴∠AOD=180°﹣∠AOC=154°,
∵OE是∠AOD的平分线,
∴∠AOE=∠DOE=∠AOD=77°,
∴∠COE=180°﹣∠DOE=103°.
20.解:(1)∵OB平分∠DOF,
∴∠BOD=∠BOF=40°,
∴∠AOC=40°;
(2)∵OB平分∠DOF,
∴∠BOD=∠BOF,
∵∠BOF=x°,
∴∠BOD=x°,
∴∠AOC=∠BOD=x°,
如图1,∵∠COE=60°,
∴∠AOE=∠AOC+∠COE=(60+x)°(0<x<90);
如图2,当0<x≤60时,
∵∠COE=60°,
∴∠AOE=∠COE﹣∠AOC=(60﹣x)°(0<x≤60),
当60<x<90时,如图3中,
∵∠COE=60°,
∴∠AOE=∠AOC+∠COE=(x+60)°(60<x<90),
或∠AOE′=∠AOC﹣∠COE′=(x﹣60)°
综上所述:∠AOE的度数为(60+x)°或|60﹣x|°.
21.解:∵∠AOC=40°,
∴∠BOC=180°﹣∠AOC=140°,
∵OE平分∠BOC,
∴∠COE=∠BOC=70°,
∴∠DOE=180°﹣∠COE=110°.
22.解:设∠BOD=2x,
∵OE平分∠BOD,
∴∠DOE=∠EOB==x,
∵∠BOC=∠DOE+75°=x+75°.
∴x+75°+2x=180°,
解得:x=35°,
∴∠BOD=2×35°=70°,
∴∠AOD=180°﹣∠BOD=180°﹣70°=110°,
∵FO⊥CD,
∴∠BOF=90°﹣∠BOD=90°﹣70°=20°,
∴∠EOF=∠FOB+∠BOE=20°+35°=55°.
所以∠AOD和∠EOF的度数分别为:110°、55°.
23.解:(1)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠2=∠1,
∴∠2+∠AOC=90°,
∴∠NOC=90°;
(2)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM=∠BOC﹣∠1=4∠1﹣∠1=90°,
∴∠1=30°,
∴∠AOC=∠AOM﹣∠1=90°﹣30°=60°.
1.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1) B.n2﹣n+1 C. D.
2.如图两条非平行的直线AB,CD被第三条直线EF所截,交点为PQ,那么这3条直线将所在平面分成( )
A.5个部分 B.6个部分 C.7个部分 D.8个部分
3.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.4 B.5 C.6 D.以上都不对
4.如图所示,∠1和∠2是对顶角的图形是( )
A.B.C.D.
5.如图,AB⊥CD,垂足为O,直线EF经过点O,若∠1=50°,则∠2=( )
A.30° B.40° C.50° D.60°
6.如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( )
A.①② B.①③ C.②③ D.①②③
7.如图,点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是( )
A.PA B.PC C.PB D.PD
8.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm B.5cm C.小于2cm D.不大于2cm
9.下列图中,∠1与∠2是同位角的是( )
A.B. C.D.
10.如图,直线l与∠BAC的两边分别相交于点D、E,则图中是同旁内角的有( )
A.2对 B.3对 C.4对 D.5对
11.四条直线两两相交,至多会有 个交点.
12.三条直线两两相交,则交点有 个.
13.平面内两直线相交有 个交点,两平面相交形成 条直线.
14.如图是一把剪刀,若∠AOB+∠COD=80°,则∠AOC= 度.
15.如图,已知AO⊥BC于O,∠BOD=120°,那么∠AOD= °.
16.如图,CD⊥AB于点D,∠EDF=90°,那么图中互补的角有 对.
17.如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.理由是 .
18.如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
19.如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=26°,求∠AOE和∠COE的度数.
20.已知,直线AB与直线CD相交于点O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(0<x<90),求∠AOE的度数.(用含x的代数式表示)
21.已知:如图,直线AB,CD相交于点O,∠AOC=40°,OE平分∠BOC,求∠DOE的度数.
22.如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,若∠BOC比∠DOE大75o.求∠AOD和∠EOF的度数.
23.如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOC的度数;
(2)若∠BOC=4∠1,求∠AOC的度数.
参考答案
1.解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;…
n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.
所以a=,而b=1,
∴a+b=.
故选:D.
2.解:因为直线是向两方无限延伸的所以应是7部分;
故选:C.
3.解:根据题意可得:3条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,3条直线相交,交点最多为3个,即n=3;
则m+n=1+3=4.
故选:A.
4.解:根据对顶角的意义,一个角的两条边分别是另一个角两边的反向延长线,这两个角是对顶角,
只有图B中的∠1和∠2是对顶角,
故选:B.
5.解:∵AB⊥CD,
∴∠BOD=90°,
∵∠BOD+∠1+∠2=180°,∠1=50°,
∴∠2=180°﹣∠BOD﹣∠1=180°﹣90°﹣50°=40°.
故选:B.
6.解:∵OE⊥CD于O,∠EOF=α,
∴∠DOF=α﹣90°,
∵OD平分∠BOF,
∴∠BOD=∠FOD,
∵∠AOC=∠BOD,
∴∠AOC=∠FOD,
∴∠AOC=α﹣90°,①正确;
∴∠BOE=180°﹣∠COE﹣∠AOC=180°﹣90°﹣(α﹣90°)=180°﹣α,②正确;
∴∠AOF=180°﹣∠AOC﹣∠DOF=180°﹣(α﹣90°)﹣(α﹣90°)=360°﹣2α,③正确;
故选:D.
7.解:由题意,得
点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是PB,
故选:C.
8.解:当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,
当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,
综上所述:点P到直线m的距离不大于2cm,
故选:D.
9.解:选项A中的两个角是同旁内角,因此不符合题意;
选项C中的两个角既不是同位角、也不是内错角、同旁内角,因此不符合题意;
选项D不是两条直线被一条直线所截出现的角,不符合题意;
只有选项B中的两个角符合同位角的意义,符合题意;
故选:B.
10.解:直线AC与直线AB被直线l所截形成的同旁内角有:∠ADE与∠AED、∠CDE与∠BED;
直线AC与直线DE被直线AB所截形成的同旁内角有:∠DAE与∠DEA;
直线AB与直线DE被直线AC所截形成的同旁内角有:∠EAD与∠EDA;
故选:C.
11.解:如图,可看出四条直线两两相交,至多有6个交点.
故填:6.
12.解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
13.解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
14.解:∵∠AOB+∠COD=80°,∠AOB=∠COD,
∴∠AOB=∠COD=40°,
又∵∠AOC+∠COD=180°,
∴∠AOC=180°﹣40°=140°,
故答案为:140.
15.解:∵AO⊥BC,
∴∠AOB=90°,
∵∠BOD=120°,
∴∠AOD=∠BOD﹣∠AOB=120°﹣90°=30°,
故答案是:30.
16.解:∠FDC与∠ADE是互补的角,∠CDE与∠FDB是互补的角,∠EDB与∠ADE是互补的角,∠ADC与∠CDB是互补的角,∠FDE与∠CDB是互补的角,∠FDE与∠ADC,∠ADF与∠BDF是互补的角.
故答案为:7.
17.解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
18.解:因为∠C=90°,
所以AC⊥BC,
所以A到BC的距离是AC,
因为线段AC=9cm,
所以点A到BC的距离为9cm.
故答案为:9.
19.解:∵∠AOC=26°,
∴∠AOD=180°﹣∠AOC=154°,
∵OE是∠AOD的平分线,
∴∠AOE=∠DOE=∠AOD=77°,
∴∠COE=180°﹣∠DOE=103°.
20.解:(1)∵OB平分∠DOF,
∴∠BOD=∠BOF=40°,
∴∠AOC=40°;
(2)∵OB平分∠DOF,
∴∠BOD=∠BOF,
∵∠BOF=x°,
∴∠BOD=x°,
∴∠AOC=∠BOD=x°,
如图1,∵∠COE=60°,
∴∠AOE=∠AOC+∠COE=(60+x)°(0<x<90);
如图2,当0<x≤60时,
∵∠COE=60°,
∴∠AOE=∠COE﹣∠AOC=(60﹣x)°(0<x≤60),
当60<x<90时,如图3中,
∵∠COE=60°,
∴∠AOE=∠AOC+∠COE=(x+60)°(60<x<90),
或∠AOE′=∠AOC﹣∠COE′=(x﹣60)°
综上所述:∠AOE的度数为(60+x)°或|60﹣x|°.
21.解:∵∠AOC=40°,
∴∠BOC=180°﹣∠AOC=140°,
∵OE平分∠BOC,
∴∠COE=∠BOC=70°,
∴∠DOE=180°﹣∠COE=110°.
22.解:设∠BOD=2x,
∵OE平分∠BOD,
∴∠DOE=∠EOB==x,
∵∠BOC=∠DOE+75°=x+75°.
∴x+75°+2x=180°,
解得:x=35°,
∴∠BOD=2×35°=70°,
∴∠AOD=180°﹣∠BOD=180°﹣70°=110°,
∵FO⊥CD,
∴∠BOF=90°﹣∠BOD=90°﹣70°=20°,
∴∠EOF=∠FOB+∠BOE=20°+35°=55°.
所以∠AOD和∠EOF的度数分别为:110°、55°.
23.解:(1)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠2=∠1,
∴∠2+∠AOC=90°,
∴∠NOC=90°;
(2)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM=∠BOC﹣∠1=4∠1﹣∠1=90°,
∴∠1=30°,
∴∠AOC=∠AOM﹣∠1=90°﹣30°=60°.
