2021-2022学年人教版七年级数学下册 5.2平行线及其判定寒假预习同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册 5.2平行线及其判定寒假预习同步练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 21:37:56 | ||
图片预览

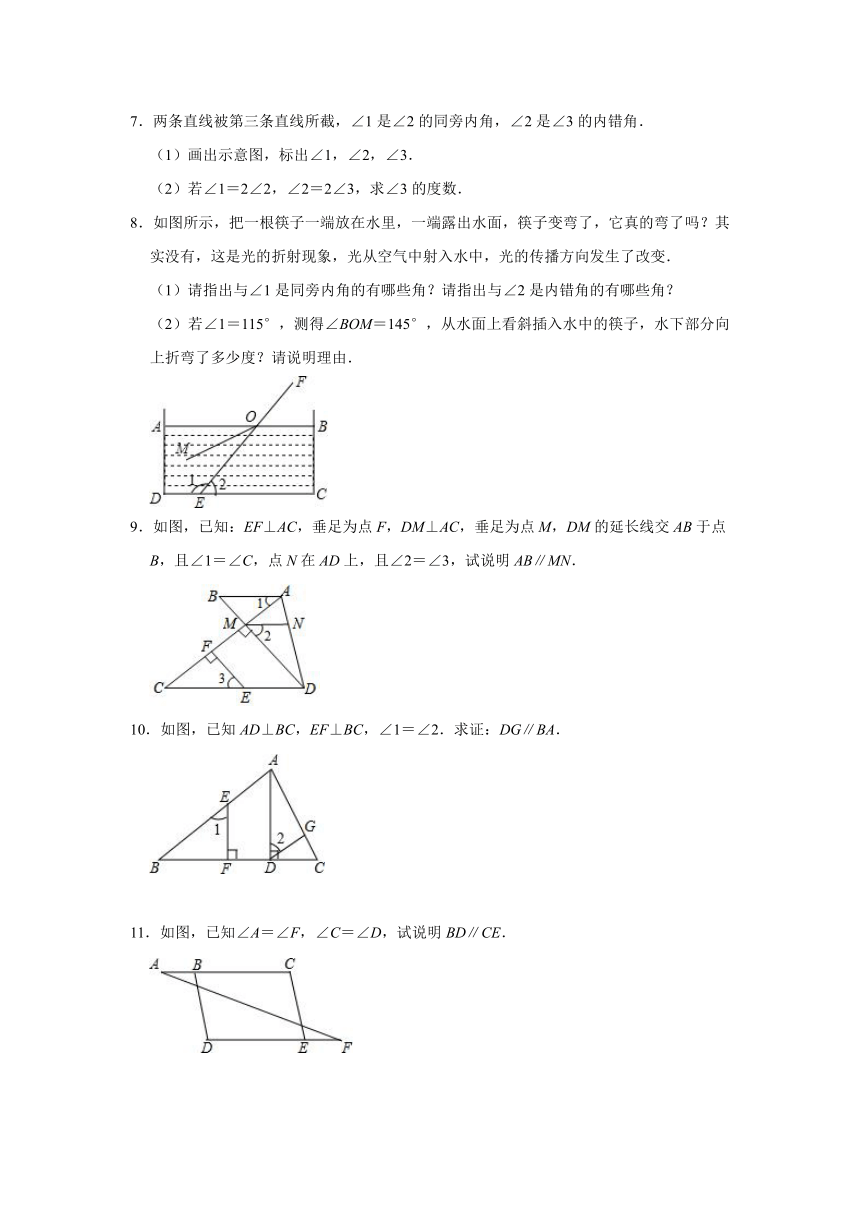
文档简介
2021-2022学年人教版七年级数学下册《5-2平行线及其判定》寒假预习同步练习(附答案)
1.如图,直线DE截AB,AC,其中内错角有( )对.
A.1 B.2 C.3 D.4
2.某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.
A.4 B.8 C.12 D.16
3.四条直线两两相交,且任意三条不相交于同一点,则四条直线共可构成的同位角有( )
A.24组 B.48组 C.12组 D.16组
4.如图两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 .
5.图中与∠1构成同位角的个数有 个.
6.如图.∠1与∠C是一对内错角,∠1与∠3是一对 角.
7.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
8.如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出与∠1是同旁内角的有哪些角?请指出与∠2是内错角的有哪些角?
(2)若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
9.如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
10.如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.
11.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
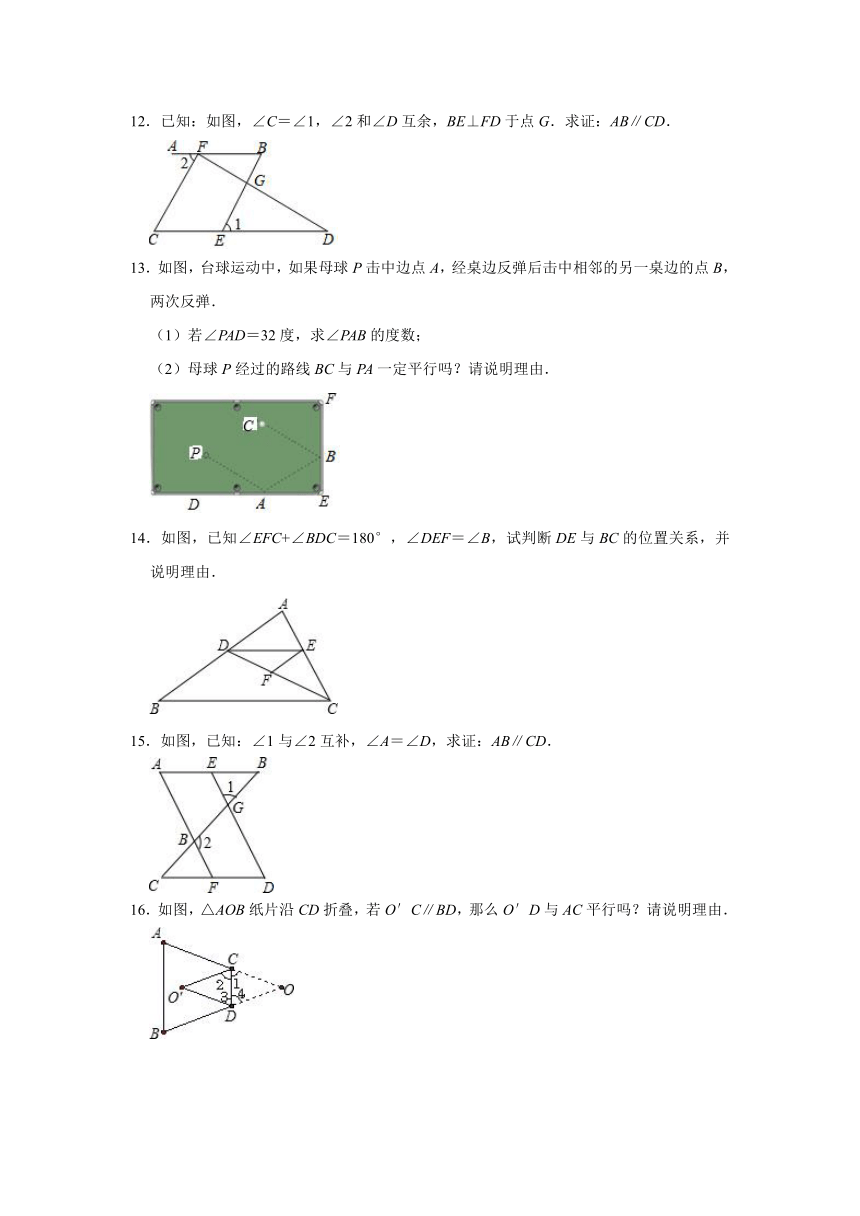
12.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.
13.如图,台球运动中,如果母球P击中边点A,经桌边反弹后击中相邻的另一桌边的点B,两次反弹.
(1)若∠PAD=32度,求∠PAB的度数;
(2)母球P经过的路线BC与PA一定平行吗?请说明理由.
14.如图,已知∠EFC+∠BDC=180°,∠DEF=∠B,试判断DE与BC的位置关系,并说明理由.
15.如图,已知:∠1与∠2互补,∠A=∠D,求证:AB∥CD.
16.如图,△AOB纸片沿CD折叠,若O′C∥BD,那么O′D与AC平行吗?请说明理由.
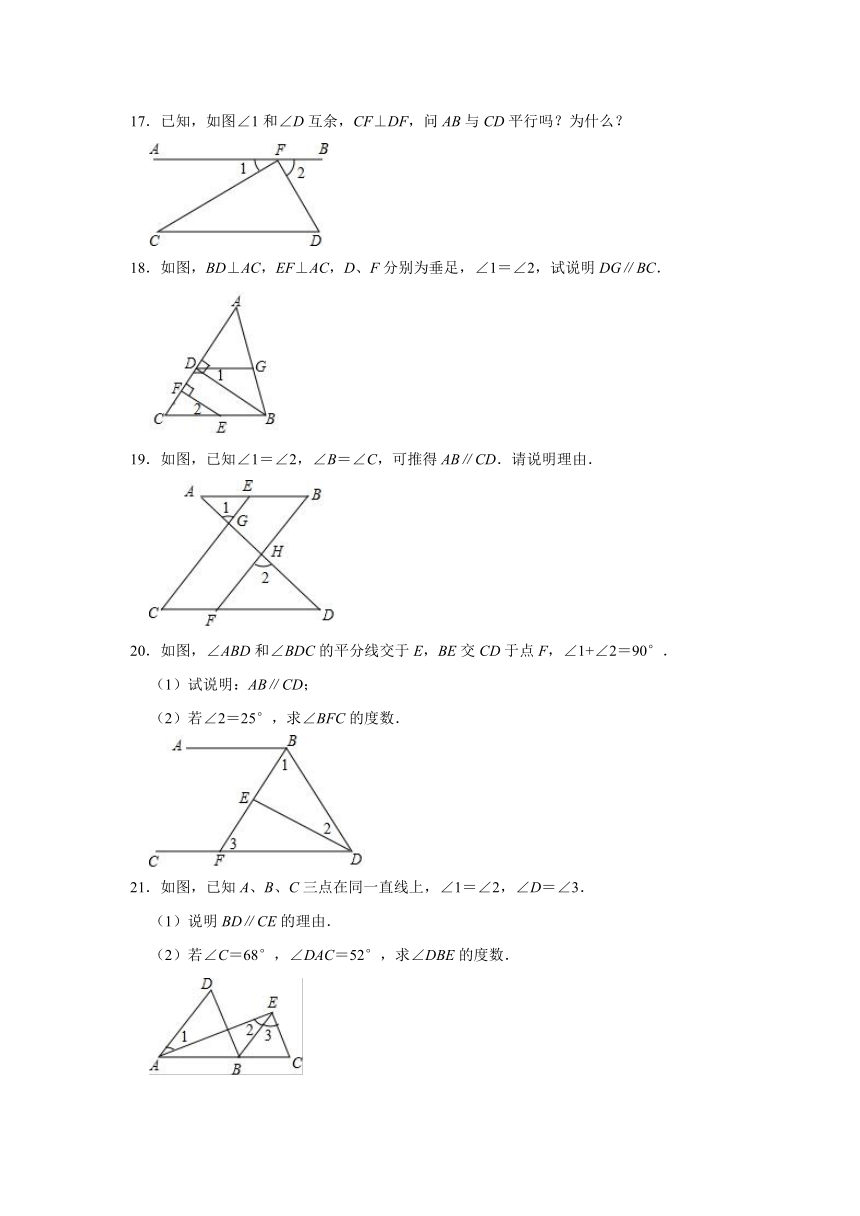
17.已知,如图∠1和∠D互余,CF⊥DF,问AB与CD平行吗?为什么?
18.如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明DG∥BC.
19.如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.请说明理由.
20.如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
21.如图,已知A、B、C三点在同一直线上,∠1=∠2,∠D=∠3.
(1)说明BD∥CE的理由.
(2)若∠C=68°,∠DAC=52°,求∠DBE的度数.
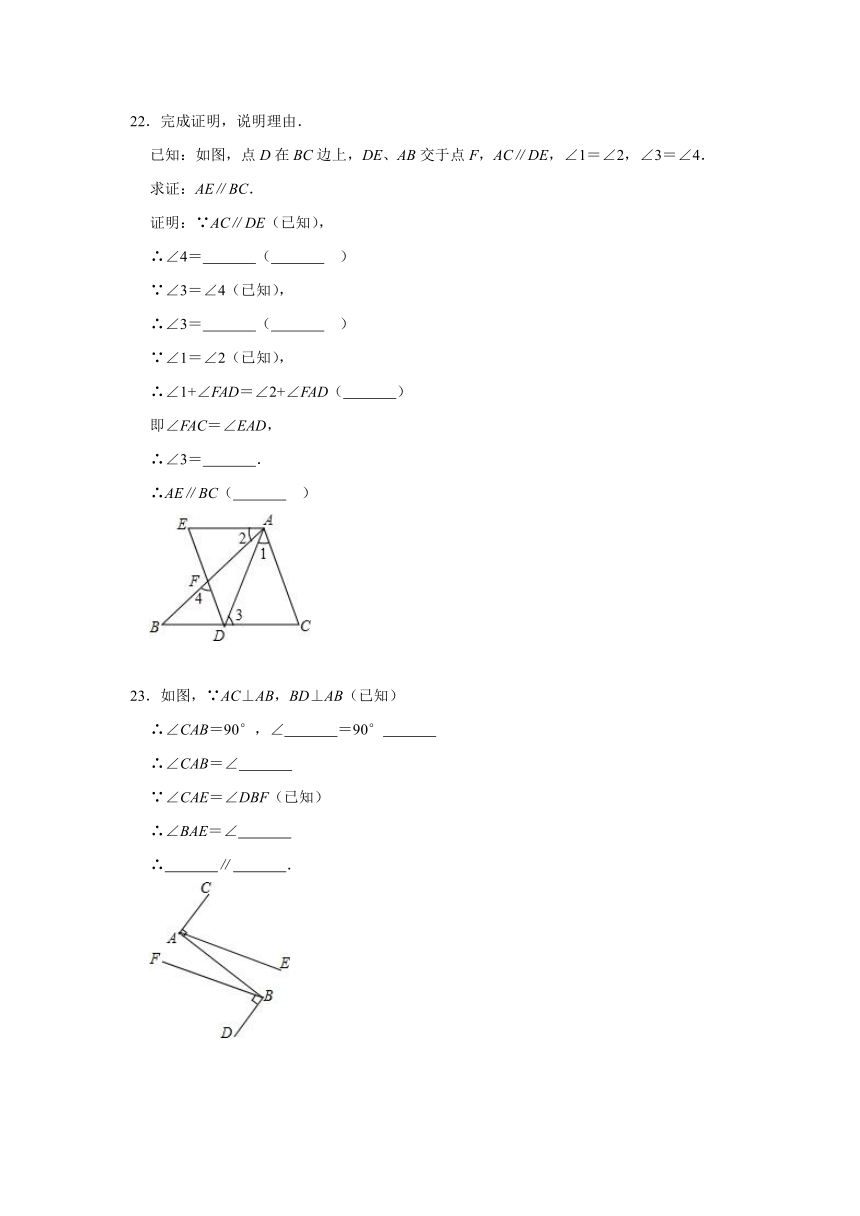
22.完成证明,说明理由.
已知:如图,点D在BC边上,DE、AB交于点F,AC∥DE,∠1=∠2,∠3=∠4.
求证:AE∥BC.
证明:∵AC∥DE(已知),
∴∠4= ( )
∵∠3=∠4(已知),
∴∠3= ( )
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD( )
即∠FAC=∠EAD,
∴∠3= .
∴AE∥BC( )
23.如图,∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=90°,∠ =90°
∴∠CAB=∠
∵∠CAE=∠DBF(已知)
∴∠BAE=∠
∴ ∥ .
24.已知:如图,∠ACD=2∠B,CE平分∠ACD.求证:CE∥AB.
25.如图,已知AD平分∠BAC,且AD⊥BC于D,点E、A、C在同一直线上,∠DAC=∠EFA,延长EF交BC于G,说明为什么EG⊥BC.
26.先作图,再证明.
(1)在所给的图形(如图)中完成下列作图(保留作图痕迹)
①作∠ACB的平分线CD,交AB于点D;
②延长BC到点E,使CE=CA,连接AE;
(2)求证:CD∥AE.
参考答案
1.解:直线DE截AB、AC,形成两对内错角,
直线AB截AC,DE,形成一对内错角;
直线AC截AB,DE,形成一对内错角.
综上,共形成4对内错角.
故选:D.
2.解:l1、l2被l3所截,有两对同旁内角,其它同理,故一共有同旁内角2×8=16对.
故选:D.
3.解:∵平面上4条直线两两相交且无三线共点,
∴共有3×4=12条线段.
又∵每条线段各有4组同位角,
∴共有同位角12×4=48组.
故选:B.
4.解:如图,设∠1=x°,则∠3=2x°,∠2=4∠3=8x°,
∵∠1+∠2=180°,
∴x°+8x°=180°,
解得:x=20,
∴∠1=20°.
故答案为:20°.
5.解:如图,由同位角的定义知,能与∠1构成同位角的角有∠2、∠3、∠4,共3个,
故答案为:3.
6.解:如图:
∠1与∠3是直线AC与AB被直线a所截形成的一对同位角.
故答案为:同位角.
7.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
8.解:(1)与∠1是同旁内角的有∠AOE,∠MOE,∠ADE;
与∠2是内错角的有∠MOE,∠AOE;
(2)∵AB∥CD,
∴∠BOE=∠1=115°,
∵∠BOM=145°,
∴∠MOE=∠BOM﹣∠BOE=145°﹣115°=30°,
∴往上弯了30°.
9.解:∵EF⊥AC,DM⊥AC,
∴∠CFE=∠CMD=90°(垂直定义),
∴EF∥DM(同位角相等,两直线平行),
∴∠3=∠CDM(两直线平行,同位角相等),
∵∠3=∠2(已知),
∴∠2=∠CDM(等量代换),
∴MN∥CD(内错角相等,两直线平行),
∴∠AMN=∠C(两直线平行,同位角相等),
∵∠1=∠C(已知),
∴∠1=∠AMN(等量代换),
∴AB∥MN(内错角相等,两直线平行).
10.证明:∵AD⊥BC,EF⊥BC,
∴∠EFB=∠ADB=90°,
∴AD∥EF,
∴∠1=∠BAD,
∵∠1=∠2,
∴∠2=∠BAD,
∴AB∥DG.
11.解:∵∠A=∠F(已知)
∴AC∥DF( 内错角相等,两直线平行 )
∴∠D=∠ABD( 两直线平行,内错角相等)
∵∠C=∠D(已知)
∴∠C=∠ABD(等量代换)
∴BD∥CE( 同位角相等,两直线平行)
12.证明:∵BE⊥FD,
∴∠EGD=90°,
∴∠1+∠D=90°,
又∠2和∠D互余,即∠2+∠D=90°,
∴∠1=∠2,
又已知∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
13.解:(1)∵∠PAD=32°,∠PAD=∠BAE,∠PAD+∠PAB+∠BAE=180°,
∴∠PAB=180°﹣32°﹣32°=116°.
(2)BC∥PA,理由如下:
∵∠PAD=∠BAE,∠PAB=180°﹣∠PAD﹣∠BAE,
∴∠PAB=180°﹣2∠BAE.
同理:∠ABC=180°﹣2∠ABE.
∵∠BAE+∠ABE=90°,
∴∠PAB+∠ABC=360°﹣2(∠BAE+∠ABE)=180°.
∴BC∥PA.
14.解:DE∥BC.
理由:∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,
∴∠EFC=∠ADC,
∴AD∥EF,
∴∠DEF=∠ADE,
又∵∠DEF=∠B,
∴∠B=∠ADE,
∴DE∥BC.
15.证明:∵∠1=∠CGD,∠1与∠2互补,
∴∠CGD+∠2=180°,
∴AF∥ED,
∴∠A+∠AED=180°,
∵∠A=∠D,
∴∠D+∠AED=180°,
∴AB∥CD.
16.解:O′D与AC平行.理由如下:
∵O′C∥BD,
∴∠2=∠4.
∵∠2=∠1,∠3=∠4,
∴∠3=∠1.
∴O′D∥AC.
17.解:AB∥CD.理由如下:
∵CF⊥DF,
∴∠CFD=90°.
∵∠1+∠CFD+∠2=180°,
∴∠1+∠2=90°.
∵∠1与∠D互余,
∴∠1+∠D=90°,
∴∠2=∠D,
∴AB∥CD(内错角相等,两直线平行).
18.证明:∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠2=∠DBC,
∵∠2=∠1,
∴∠1=∠DBC,
∴DG∥BC.
19.证明:如图,∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴CE∥BF,
∴∠C=∠BFD,
∵∠B=∠C,
∴∠B=∠BFD,
∴AB∥CD.
20.解:(1)∵∠ABD和∠BDC的平分线交于E,
∴∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥CD;
(2)∵DE平分∠BDC,
∴∠EDF=∠2=25°,
∵∠1+∠2=90°,
∴∠FED=90°,
∴∠3=180°﹣90°﹣25°=65°.
∴∠BFC=180°﹣∠3=115°.
21.解:(1)∵∠1=∠2
∴AD∥BE,
∴∠D=∠DBE,
∵∠3=∠D,
∴∠3=∠DBE,
∴BD∥CE;
(2)∵AD∥BE
∴∠EBC=∠DAC=52°,
又∵BD∥CE
∴∠ABD=∠C=68°,
∵∠ABD+∠DBE+∠EBC=180°
∴∠DBE=180°﹣∠ABD﹣∠EBC=60°,
22.解:∵AC∥DE(已知),
∴∠4=∠FAC(两直线平行,同位角相等)
∵∠3=∠4(已知),
∴∠3=∠FAC(等量代换)
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD(等式的性质)
即∠FAC=∠EAD,
∴∠3=∠EAD.
∴AE∥BC(内错角相等,两直线平行 ).
故答案为:∠FAC;两直线平行,同位角相等;∠FAC;等量代换;等式的性质;∠EAD;内错角相等,两直线平行.
23.解:∵AC⊥AB,BD⊥AB(已知),
∴∠CAB=90°,∠DBA=90°(垂直定义),
∴∠CAB=∠ABD,
∵∠CAE=∠DBF(已知)
∴∠BAE=∠ABF,
∴AE∥BF.
24.证明:∵CE平分∠ACD,
∴∠ACD=2∠DCE,
∵∠ACD=2∠B,
∴∠DCE=∠B,
∴AB∥CE.
25.解:∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠DAC=∠EFA,
∴∠BAD=∠DAC=∠EFA,
∴EG∥AD,
∵AD⊥BC,
∴EG⊥BC.
26.(1)解:利用尺规作图,如右图;
①1.以∠ACB的顶点C为圆心O,任意长为半径画弧.交于两边于点G,F;
2.截取GF长度,以GF长为半径,分别以点G,点F为圆心画弧,两弧交点为点D;
3.连接CD.
射线CD就是所要求作的.
②延长BC到点E,使CE=CA,连接AE.
(2)证明:∵AC=CE,AC⊥CE,
∴△ACE为等腰直角三角形,
∴∠CAE=45°.
又∵CD平分∠ACB.
∴∠ACD=45°.
∴∠ACD=∠CAE.
∴CD∥AE.
1.如图,直线DE截AB,AC,其中内错角有( )对.
A.1 B.2 C.3 D.4
2.某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.
A.4 B.8 C.12 D.16
3.四条直线两两相交,且任意三条不相交于同一点,则四条直线共可构成的同位角有( )
A.24组 B.48组 C.12组 D.16组
4.如图两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是 .
5.图中与∠1构成同位角的个数有 个.
6.如图.∠1与∠C是一对内错角,∠1与∠3是一对 角.
7.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
8.如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出与∠1是同旁内角的有哪些角?请指出与∠2是内错角的有哪些角?
(2)若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
9.如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
10.如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.
11.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
12.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.
13.如图,台球运动中,如果母球P击中边点A,经桌边反弹后击中相邻的另一桌边的点B,两次反弹.
(1)若∠PAD=32度,求∠PAB的度数;
(2)母球P经过的路线BC与PA一定平行吗?请说明理由.
14.如图,已知∠EFC+∠BDC=180°,∠DEF=∠B,试判断DE与BC的位置关系,并说明理由.
15.如图,已知:∠1与∠2互补,∠A=∠D,求证:AB∥CD.
16.如图,△AOB纸片沿CD折叠,若O′C∥BD,那么O′D与AC平行吗?请说明理由.
17.已知,如图∠1和∠D互余,CF⊥DF,问AB与CD平行吗?为什么?
18.如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明DG∥BC.
19.如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.请说明理由.
20.如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
21.如图,已知A、B、C三点在同一直线上,∠1=∠2,∠D=∠3.
(1)说明BD∥CE的理由.
(2)若∠C=68°,∠DAC=52°,求∠DBE的度数.
22.完成证明,说明理由.
已知:如图,点D在BC边上,DE、AB交于点F,AC∥DE,∠1=∠2,∠3=∠4.
求证:AE∥BC.
证明:∵AC∥DE(已知),
∴∠4= ( )
∵∠3=∠4(已知),
∴∠3= ( )
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD( )
即∠FAC=∠EAD,
∴∠3= .
∴AE∥BC( )
23.如图,∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=90°,∠ =90°
∴∠CAB=∠
∵∠CAE=∠DBF(已知)
∴∠BAE=∠
∴ ∥ .
24.已知:如图,∠ACD=2∠B,CE平分∠ACD.求证:CE∥AB.
25.如图,已知AD平分∠BAC,且AD⊥BC于D,点E、A、C在同一直线上,∠DAC=∠EFA,延长EF交BC于G,说明为什么EG⊥BC.
26.先作图,再证明.
(1)在所给的图形(如图)中完成下列作图(保留作图痕迹)
①作∠ACB的平分线CD,交AB于点D;
②延长BC到点E,使CE=CA,连接AE;
(2)求证:CD∥AE.
参考答案
1.解:直线DE截AB、AC,形成两对内错角,
直线AB截AC,DE,形成一对内错角;
直线AC截AB,DE,形成一对内错角.
综上,共形成4对内错角.
故选:D.
2.解:l1、l2被l3所截,有两对同旁内角,其它同理,故一共有同旁内角2×8=16对.
故选:D.
3.解:∵平面上4条直线两两相交且无三线共点,
∴共有3×4=12条线段.
又∵每条线段各有4组同位角,
∴共有同位角12×4=48组.
故选:B.
4.解:如图,设∠1=x°,则∠3=2x°,∠2=4∠3=8x°,
∵∠1+∠2=180°,
∴x°+8x°=180°,
解得:x=20,
∴∠1=20°.
故答案为:20°.
5.解:如图,由同位角的定义知,能与∠1构成同位角的角有∠2、∠3、∠4,共3个,
故答案为:3.
6.解:如图:
∠1与∠3是直线AC与AB被直线a所截形成的一对同位角.
故答案为:同位角.
7.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
8.解:(1)与∠1是同旁内角的有∠AOE,∠MOE,∠ADE;
与∠2是内错角的有∠MOE,∠AOE;
(2)∵AB∥CD,
∴∠BOE=∠1=115°,
∵∠BOM=145°,
∴∠MOE=∠BOM﹣∠BOE=145°﹣115°=30°,
∴往上弯了30°.
9.解:∵EF⊥AC,DM⊥AC,
∴∠CFE=∠CMD=90°(垂直定义),
∴EF∥DM(同位角相等,两直线平行),
∴∠3=∠CDM(两直线平行,同位角相等),
∵∠3=∠2(已知),
∴∠2=∠CDM(等量代换),
∴MN∥CD(内错角相等,两直线平行),
∴∠AMN=∠C(两直线平行,同位角相等),
∵∠1=∠C(已知),
∴∠1=∠AMN(等量代换),
∴AB∥MN(内错角相等,两直线平行).
10.证明:∵AD⊥BC,EF⊥BC,
∴∠EFB=∠ADB=90°,
∴AD∥EF,
∴∠1=∠BAD,
∵∠1=∠2,
∴∠2=∠BAD,
∴AB∥DG.
11.解:∵∠A=∠F(已知)
∴AC∥DF( 内错角相等,两直线平行 )
∴∠D=∠ABD( 两直线平行,内错角相等)
∵∠C=∠D(已知)
∴∠C=∠ABD(等量代换)
∴BD∥CE( 同位角相等,两直线平行)
12.证明:∵BE⊥FD,
∴∠EGD=90°,
∴∠1+∠D=90°,
又∠2和∠D互余,即∠2+∠D=90°,
∴∠1=∠2,
又已知∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
13.解:(1)∵∠PAD=32°,∠PAD=∠BAE,∠PAD+∠PAB+∠BAE=180°,
∴∠PAB=180°﹣32°﹣32°=116°.
(2)BC∥PA,理由如下:
∵∠PAD=∠BAE,∠PAB=180°﹣∠PAD﹣∠BAE,
∴∠PAB=180°﹣2∠BAE.
同理:∠ABC=180°﹣2∠ABE.
∵∠BAE+∠ABE=90°,
∴∠PAB+∠ABC=360°﹣2(∠BAE+∠ABE)=180°.
∴BC∥PA.
14.解:DE∥BC.
理由:∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,
∴∠EFC=∠ADC,
∴AD∥EF,
∴∠DEF=∠ADE,
又∵∠DEF=∠B,
∴∠B=∠ADE,
∴DE∥BC.
15.证明:∵∠1=∠CGD,∠1与∠2互补,
∴∠CGD+∠2=180°,
∴AF∥ED,
∴∠A+∠AED=180°,
∵∠A=∠D,
∴∠D+∠AED=180°,
∴AB∥CD.
16.解:O′D与AC平行.理由如下:
∵O′C∥BD,
∴∠2=∠4.
∵∠2=∠1,∠3=∠4,
∴∠3=∠1.
∴O′D∥AC.
17.解:AB∥CD.理由如下:
∵CF⊥DF,
∴∠CFD=90°.
∵∠1+∠CFD+∠2=180°,
∴∠1+∠2=90°.
∵∠1与∠D互余,
∴∠1+∠D=90°,
∴∠2=∠D,
∴AB∥CD(内错角相等,两直线平行).
18.证明:∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠2=∠DBC,
∵∠2=∠1,
∴∠1=∠DBC,
∴DG∥BC.
19.证明:如图,∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴CE∥BF,
∴∠C=∠BFD,
∵∠B=∠C,
∴∠B=∠BFD,
∴AB∥CD.
20.解:(1)∵∠ABD和∠BDC的平分线交于E,
∴∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥CD;
(2)∵DE平分∠BDC,
∴∠EDF=∠2=25°,
∵∠1+∠2=90°,
∴∠FED=90°,
∴∠3=180°﹣90°﹣25°=65°.
∴∠BFC=180°﹣∠3=115°.
21.解:(1)∵∠1=∠2
∴AD∥BE,
∴∠D=∠DBE,
∵∠3=∠D,
∴∠3=∠DBE,
∴BD∥CE;
(2)∵AD∥BE
∴∠EBC=∠DAC=52°,
又∵BD∥CE
∴∠ABD=∠C=68°,
∵∠ABD+∠DBE+∠EBC=180°
∴∠DBE=180°﹣∠ABD﹣∠EBC=60°,
22.解:∵AC∥DE(已知),
∴∠4=∠FAC(两直线平行,同位角相等)
∵∠3=∠4(已知),
∴∠3=∠FAC(等量代换)
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD(等式的性质)
即∠FAC=∠EAD,
∴∠3=∠EAD.
∴AE∥BC(内错角相等,两直线平行 ).
故答案为:∠FAC;两直线平行,同位角相等;∠FAC;等量代换;等式的性质;∠EAD;内错角相等,两直线平行.
23.解:∵AC⊥AB,BD⊥AB(已知),
∴∠CAB=90°,∠DBA=90°(垂直定义),
∴∠CAB=∠ABD,
∵∠CAE=∠DBF(已知)
∴∠BAE=∠ABF,
∴AE∥BF.
24.证明:∵CE平分∠ACD,
∴∠ACD=2∠DCE,
∵∠ACD=2∠B,
∴∠DCE=∠B,
∴AB∥CE.
25.解:∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠DAC=∠EFA,
∴∠BAD=∠DAC=∠EFA,
∴EG∥AD,
∵AD⊥BC,
∴EG⊥BC.
26.(1)解:利用尺规作图,如右图;
①1.以∠ACB的顶点C为圆心O,任意长为半径画弧.交于两边于点G,F;
2.截取GF长度,以GF长为半径,分别以点G,点F为圆心画弧,两弧交点为点D;
3.连接CD.
射线CD就是所要求作的.
②延长BC到点E,使CE=CA,连接AE.
(2)证明:∵AC=CE,AC⊥CE,
∴△ACE为等腰直角三角形,
∴∠CAE=45°.
又∵CD平分∠ACB.
∴∠ACD=45°.
∴∠ACD=∠CAE.
∴CD∥AE.
