浙江省浙南名校联盟2021-2022学年高三上学期期末联考数学试题(Word版含答案)
文档属性
| 名称 | 浙江省浙南名校联盟2021-2022学年高三上学期期末联考数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 888.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 18:32:12 | ||
图片预览




文档简介
浙南名校联盟2021-2022学年高三上学期期末联考
数学试题
选择题部分
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知,,则( )
A. B.
C. D.
2.已知双曲线的离心率为,则其渐近线方程是( )
A. B. C. D.
3.若复数满足,(其中为虚数单位)则的值为( )
A.1 B. C.2 D.
4.已知“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.某几何体的三视图如图所示(单位:),则该几何体的体积(单位:)是( )
A.12 B.6 C.4 D.2
6.已知成等差数列,也成等差数列,则的值为( )
A. B. C. D.
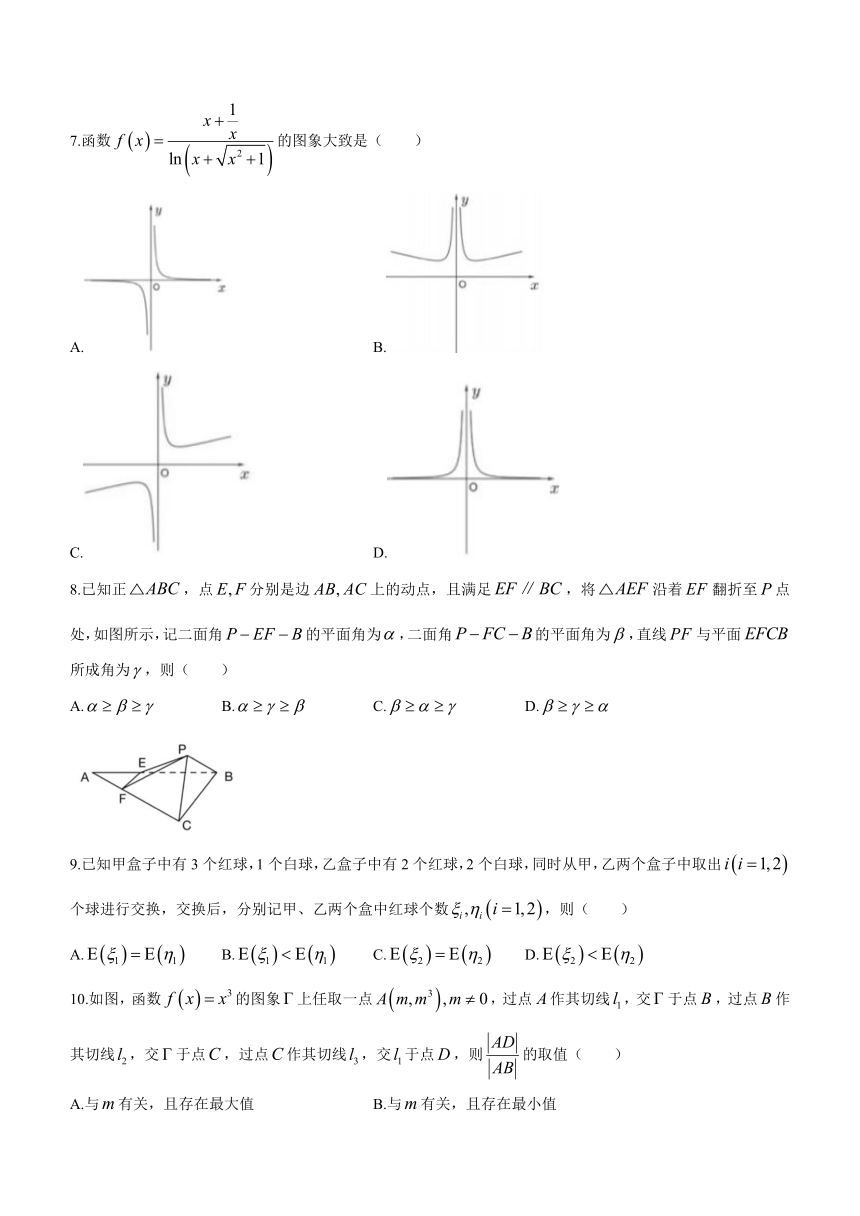
7.函数的图象大致是( )
A. B.
C. D.
8.已知正,点分别是边上的动点,且满足,将沿着翻折至点处,如图所示,记二面角的平面角为,二面角的平面角为,直线与平面所成角为,则( )
A. B. C. D.
9.已知甲盒子中有3个红球,1个白球,乙盒子中有2个红球,2个白球,同时从甲,乙两个盒子中取出个球进行交换,交换后,分别记甲、乙两个盒中红球个数,则( )
A. B. C. D.
10.如图,函数的图象上任取一点,过点作其切线,交于点,过点作其切线,交于点,过点作其切线,交于点,则的取值( )
A.与有关,且存在最大值 B.与有关,且存在最小值
C.与有关,但无最值 D.与无关,为定值
非选择题部分
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分
11.我国古代数学著作《田亩比类乘除捷法》中有这样一个问题:“给银八百六十四两,只云所得银之两数比总分人数,其银多十二两.问总是几人,每人各得几两”,其意思是:“现一共有银子八百六十四两,只知道每个人分到的银子数目的两倍比总人数多十二,则一共有____________人,每个人分得____________两银子”.
12.已知展开式中所有项系数和为1,则实数的值为____________,的系数为____________.
13.已知函数,则____________;若函数有3个零点,则实数的取值范围为____________.
14.若实数满足约束条件,则的取值范围为____________.
15.已知椭圆的右焦点,直线与椭圆交于两点(点在第一象限),且(为坐标原点),则椭圆的离心率为____________.
16.若函数与有相同的零点,其中,且在上有且只有一个零点,则的值为____________,实数的最小值为____________.
17.已知平面向量满足,,向量满足,当与的夹角余弦值取得最小值时,实数的值为____________.
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.(14分)已知函数.
(I)求函数的单调递增区间;
(II)在中,分别是角的对边,,若为上一点,且满足____________,求的面积.
请从(1);(2)为的中线,且;(3)为的角平分线,且.这三个条件中任意选一个补充到横线处并作答.(注:如果选择多个条件分别解答,按第一个解答计分)
19.(15分)如图,四棱锥中,底面为平行四边形,,为三角形,,
(I)证明:;
(II)求与平面所成角的正弦值.
20.(15分)已知数列的前项和为,数列满足,
(I)求数列与的通项公式;
(II)若,对恒成立,求实数的取值范围.
21.(15分)已知抛物线上一点到其焦点的距离为5.
(I)求与的值;
(II)过点作斜率存在的直线与拋物线交于两点(异于原点),为在轴上的投影,连接与分别交抛物线于,问:直线是否过定点,若存在,求出该定点,若不存在,请说明理由.
22.(15分)设实数,且,函数.
(I)求函数的单调区间;
(II)若函数有两个不同的零点,
(i)求的取值范围;
(ii)证明:.
绝密★考试结束前
浙南名校联盟2021-2022学年高三上学期期末联考
数学学科 试题答案及评分标准
一、选择题
1.B 2.A 3.B 4.B 5.C 6.D 7.B 8.A 9.C 10.D
第10题
解析:先证函数的图象上任取一点,,过点作其切线,交于点,过点作,交于另两个点,,则.
证明:设过点的直线为,
联立得:,
得方程,(*)
则方程(*)必有一根,于是方程(*)可改写为,(**)
当与相切于点时,方程(**)有双重根,于是;
当与相交于,点时,方程(**)有另两个根,,韦达定理知.故
接下来,连结,交于另一点,由对称性,,有上述结论,则,
所以;
连结,交于另一点,由对称性,,有上述结论,则,所以.
于是直线为,直线为,
联立得:,
所以,
故选D,与无关.
二、填空题
11.36,24 12., 13.16, 14.
15. 16., 17.
17.解析:法一:取,,,、分别是线段,的中点,要使得最大,点在线段上,则取圆过点、且与线段相切于点,此时取得最大,由切割线定理得,又,
∴,∴
法二:建立直角坐标系,为线段中点,当取得最大时,点应在线段上,设点,
则,,
取,
当时,即,后面同解法一.
三、解答题
解:(Ⅰ)
令,
∴函数的单调递增区间为,
(Ⅱ)
,
若选①:由题意知,,,故
所以
易求得故
若选②:由余弦定理得
解法1.在中,
在中,
,
故
解法2.
若选③:由题意知,,,
19.解:(1)取为中点,连接和,易得,,
所以面,又面,所以.
(2)解法一:如图所示,建立空间直角坐标系,为中点,易得,
,,,,
设点坐为面的一个法向量,
则有,得
取,设与面所成角为,则有
所以与面所成角的正弦值
解法二:易得,
有,可得点到面的距离,
设与面所成角为,则有,
所以与面所成角的正弦值
20.解:(1)解法一:,∴
又
∴
∴
由
∴
∴
(1)解法二:,
又,
∴
∴
由
∴
∴
(2)
∴
∴
当为偶数时,;当为奇数时
∴
21.解析:(1)根据抛物线的定义得:,
将点代入抛物线方程得:,
(2)设,,,,
直线的方程为.
代入抛物线方程得:.得
由题得,设过点的直线方程为,
代入抛物线方程得:,
∴,
又由己知可得直线的方程为:,
整理得:,
将和代入直线方程得:
代入上式可得:
即,得
所以直线过定点
22.解:(I),
当时,,在为递增函数
当时,令,得,
,,,
所以在为递减函数,在为递增函数.
(II)(i)解一:由(1)知,时,为极小值点,
又函数有两个零点得.
于是
得
此时,,,
故,函数有两个不同的零
(i)解法二:令
记,,令,
则在递增,在递减,且,,
当,,
当,
由已知函数有两个不同的零点,
所以,得
(ii)证明:由则
得
于是
设的极值点为,又由,于是
由对数均值不等式得.
则,所以,
欲证,
只需证,
只需证
又由,所以只需证
由,所以上述只需证
只需证
又有,又在上单调递增,
所以,所以上述不等式成立
数学试题
选择题部分
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知,,则( )
A. B.
C. D.
2.已知双曲线的离心率为,则其渐近线方程是( )
A. B. C. D.
3.若复数满足,(其中为虚数单位)则的值为( )
A.1 B. C.2 D.
4.已知“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.某几何体的三视图如图所示(单位:),则该几何体的体积(单位:)是( )
A.12 B.6 C.4 D.2
6.已知成等差数列,也成等差数列,则的值为( )
A. B. C. D.
7.函数的图象大致是( )
A. B.
C. D.
8.已知正,点分别是边上的动点,且满足,将沿着翻折至点处,如图所示,记二面角的平面角为,二面角的平面角为,直线与平面所成角为,则( )
A. B. C. D.
9.已知甲盒子中有3个红球,1个白球,乙盒子中有2个红球,2个白球,同时从甲,乙两个盒子中取出个球进行交换,交换后,分别记甲、乙两个盒中红球个数,则( )
A. B. C. D.
10.如图,函数的图象上任取一点,过点作其切线,交于点,过点作其切线,交于点,过点作其切线,交于点,则的取值( )
A.与有关,且存在最大值 B.与有关,且存在最小值
C.与有关,但无最值 D.与无关,为定值
非选择题部分
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分
11.我国古代数学著作《田亩比类乘除捷法》中有这样一个问题:“给银八百六十四两,只云所得银之两数比总分人数,其银多十二两.问总是几人,每人各得几两”,其意思是:“现一共有银子八百六十四两,只知道每个人分到的银子数目的两倍比总人数多十二,则一共有____________人,每个人分得____________两银子”.
12.已知展开式中所有项系数和为1,则实数的值为____________,的系数为____________.
13.已知函数,则____________;若函数有3个零点,则实数的取值范围为____________.
14.若实数满足约束条件,则的取值范围为____________.
15.已知椭圆的右焦点,直线与椭圆交于两点(点在第一象限),且(为坐标原点),则椭圆的离心率为____________.
16.若函数与有相同的零点,其中,且在上有且只有一个零点,则的值为____________,实数的最小值为____________.
17.已知平面向量满足,,向量满足,当与的夹角余弦值取得最小值时,实数的值为____________.
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤.
18.(14分)已知函数.
(I)求函数的单调递增区间;
(II)在中,分别是角的对边,,若为上一点,且满足____________,求的面积.
请从(1);(2)为的中线,且;(3)为的角平分线,且.这三个条件中任意选一个补充到横线处并作答.(注:如果选择多个条件分别解答,按第一个解答计分)
19.(15分)如图,四棱锥中,底面为平行四边形,,为三角形,,
(I)证明:;
(II)求与平面所成角的正弦值.
20.(15分)已知数列的前项和为,数列满足,
(I)求数列与的通项公式;
(II)若,对恒成立,求实数的取值范围.
21.(15分)已知抛物线上一点到其焦点的距离为5.
(I)求与的值;
(II)过点作斜率存在的直线与拋物线交于两点(异于原点),为在轴上的投影,连接与分别交抛物线于,问:直线是否过定点,若存在,求出该定点,若不存在,请说明理由.
22.(15分)设实数,且,函数.
(I)求函数的单调区间;
(II)若函数有两个不同的零点,
(i)求的取值范围;
(ii)证明:.
绝密★考试结束前
浙南名校联盟2021-2022学年高三上学期期末联考
数学学科 试题答案及评分标准
一、选择题
1.B 2.A 3.B 4.B 5.C 6.D 7.B 8.A 9.C 10.D
第10题
解析:先证函数的图象上任取一点,,过点作其切线,交于点,过点作,交于另两个点,,则.
证明:设过点的直线为,
联立得:,
得方程,(*)
则方程(*)必有一根,于是方程(*)可改写为,(**)
当与相切于点时,方程(**)有双重根,于是;
当与相交于,点时,方程(**)有另两个根,,韦达定理知.故
接下来,连结,交于另一点,由对称性,,有上述结论,则,
所以;
连结,交于另一点,由对称性,,有上述结论,则,所以.
于是直线为,直线为,
联立得:,
所以,
故选D,与无关.
二、填空题
11.36,24 12., 13.16, 14.
15. 16., 17.
17.解析:法一:取,,,、分别是线段,的中点,要使得最大,点在线段上,则取圆过点、且与线段相切于点,此时取得最大,由切割线定理得,又,
∴,∴
法二:建立直角坐标系,为线段中点,当取得最大时,点应在线段上,设点,
则,,
取,
当时,即,后面同解法一.
三、解答题
解:(Ⅰ)
令,
∴函数的单调递增区间为,
(Ⅱ)
,
若选①:由题意知,,,故
所以
易求得故
若选②:由余弦定理得
解法1.在中,
在中,
,
故
解法2.
若选③:由题意知,,,
19.解:(1)取为中点,连接和,易得,,
所以面,又面,所以.
(2)解法一:如图所示,建立空间直角坐标系,为中点,易得,
,,,,
设点坐为面的一个法向量,
则有,得
取,设与面所成角为,则有
所以与面所成角的正弦值
解法二:易得,
有,可得点到面的距离,
设与面所成角为,则有,
所以与面所成角的正弦值
20.解:(1)解法一:,∴
又
∴
∴
由
∴
∴
(1)解法二:,
又,
∴
∴
由
∴
∴
(2)
∴
∴
当为偶数时,;当为奇数时
∴
21.解析:(1)根据抛物线的定义得:,
将点代入抛物线方程得:,
(2)设,,,,
直线的方程为.
代入抛物线方程得:.得
由题得,设过点的直线方程为,
代入抛物线方程得:,
∴,
又由己知可得直线的方程为:,
整理得:,
将和代入直线方程得:
代入上式可得:
即,得
所以直线过定点
22.解:(I),
当时,,在为递增函数
当时,令,得,
,,,
所以在为递减函数,在为递增函数.
(II)(i)解一:由(1)知,时,为极小值点,
又函数有两个零点得.
于是
得
此时,,,
故,函数有两个不同的零
(i)解法二:令
记,,令,
则在递增,在递减,且,,
当,,
当,
由已知函数有两个不同的零点,
所以,得
(ii)证明:由则
得
于是
设的极值点为,又由,于是
由对数均值不等式得.
则,所以,
欲证,
只需证,
只需证
又由,所以只需证
由,所以上述只需证
只需证
又有,又在上单调递增,
所以,所以上述不等式成立
同课章节目录
