2022年小升初数学总复习(通用版)第8课时 比和比例(包含正比例和反比例)课件(53张PPT)
文档属性
| 名称 | 2022年小升初数学总复习(通用版)第8课时 比和比例(包含正比例和反比例)课件(53张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 15:59:00 | ||
图片预览










文档简介
(共53张PPT)
2
0
2
2
2022年小升初数学复习
全国通用版
专题四 比和比例
第8课时 比和比例(包含正比例和反比例)
考点知识梳理
热门考点精讲
目录
小考真题演练
考点知识梳理
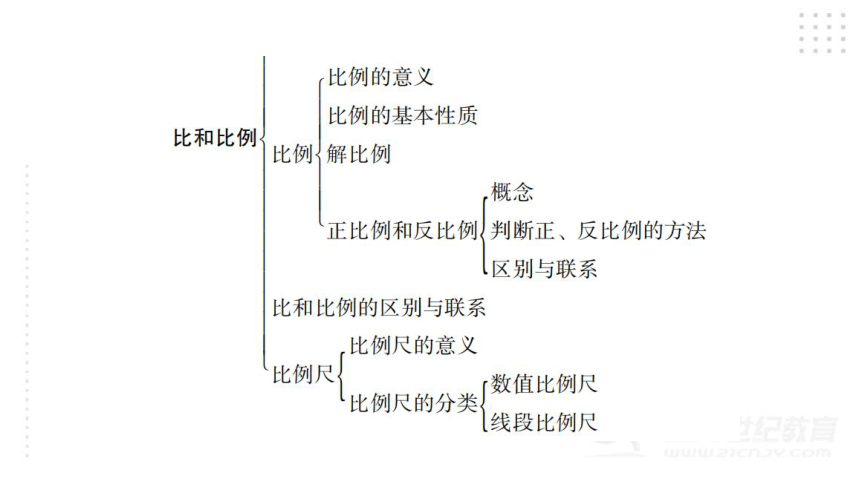
1. 比
(1)比的意义
两个数相除又叫做两个数的比。
(2)比的读法、写法和各部分的名称
在一个比中,“:”是比号,读作“比”。比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
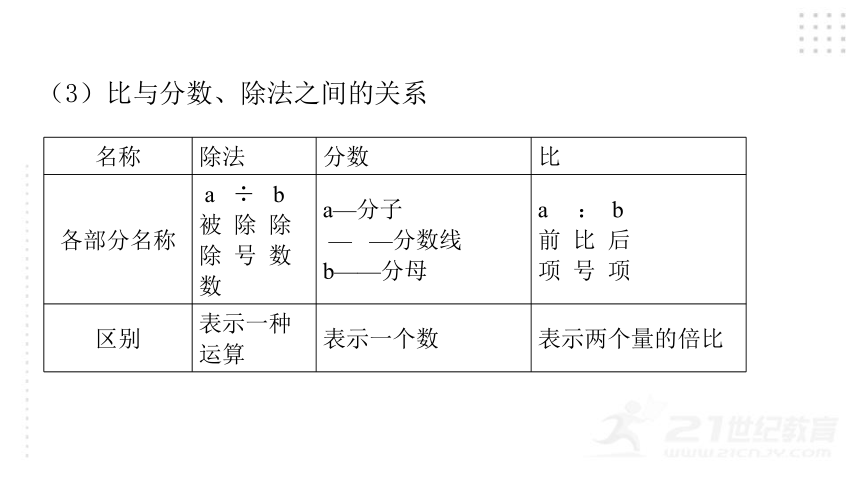
(3)比与分数、除法之间的关系
名称 除法 分数 比
各部分名称 a ÷ b 被 除 除 除 号 数 数 a—分子 — —分数线 b——分母 a : b
前 比 后
项 号 项
区别 表示一种运算 表示一个数 表示两个量的倍比
(4)比的基本性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
(5)求比值和化简比
①最简整数比:比的前项和后项都是整数,并且其公因数只有1,这样的比就是最简整数比。
②求比值的方法:用比的前项除以后项所得的商,它的结果是一个数值,这个数值可以是整数,也可以是小数或分数。
③化简比:根据比的基本性质可以把比化成最简整数比,即比的前、后项是互质的数。
(6)比的应用
按比例分配问题:把一个数量按照一定的比分配成几部分,求每部分数量各是多少的问题叫做按比例分配问题。
方法:首先求出各部分占总量的几分之几,然后求出总量的几分之几是多少。
2. 比例
(1) 比例的意义
表示两个比相等的式子叫做比例。组成比例的四个数,叫做比例的项。两端的两项叫做外项,中间的两项叫做内项。
(2)比例的基本性质
在比例里,两个外项的积等于两个内向的积,这叫做比例的基本性质。
(3)解比例
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
(4)正比例和反比例
① 成正比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。用字母表示为=k(一定)。
②成反比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用字母表示为xy=k(一定)。
③判断正、反比例的方法
判断正、反比例可总结为“一找、二看、三判断”,如下。
找变量:分析数量关系,确定哪两种量是相关联的量。
看定量:分析这两种相关联的量,它们之间的关系是商一定还是积一定。
判断:如果商一定,就成正比例;如果积一定,就成反比例;如果商和积都不是定量,就不成比例。
④正、反比例的区别与联系
名称 不同点 相同点
意义不同 变化方向不同 关系式不同 正比例 两种相关联量中,相对应的两个数的比值,也就是商一定 一种量扩大(或缩小),另一种量也随之扩大(或缩小) =k(一定) 两种相关联的量,一种量变化,另一种量也随之变化
反比例 两种相关联量中,相对应的两个数的乘积一定 一种量扩大(或缩小),另一种量反而随之缩小(或扩大) xy=k(一定) 3. 比和比例的区别与联系
名称 比 比例
意义 表示两数相除 表示两个比相等的式子
各部分 名称 5 ∶ 8 前 比 后 项 号 项 10 ∶ 16 = 5 ∶8
外 内 内 外
项 项 项 项
基本性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变 在比例里,两个外项的积等于两个内项的积
化简比的依据 解比例的依据
热门考点精讲
考点1:写出两个量的比
写出两个量的比。
(1)甲仓库的与乙仓库的相等,甲、乙两个仓库的存粮的比是( )。
(2)从甲地走向乙地,小亮走完需要12分钟,小明走完需要8分钟。小亮和小明所用时间的比是( ),他们的速度比是( )。
方法指导:此题考查比的意义。(1)假设甲仓库的与乙仓库的都是1,可用除法求出甲、乙两个仓库的存粮,进而作比即可。(2)根据路程、时间、速度的关系,求出各自的速度,再利用比的性质化简比。
答案:(1)4 ∶5 (2)3 ∶22 ∶3
1. 已知A是B的2.4倍,那么A ∶B=( ) ∶( )。
2. 一项工程,甲单独做要10天完成,乙单独做要12天完成,甲、乙的工作效率比是( ) ∶( )。
12
5
6
5
3. 已知小圆的半径是2 cm,大圆的半径是3 cm,小圆和大圆的周长比是( ) ∶( ),面积比是( ) ∶( )。
易错点拨:写两数的比时,没有写成最简整数比。
2
3
4
9
考点2:化简比
化简下列各比:
(1)32 ∶40
(2)1.25 ∶ 2.5
(3) ∶
方法指导:化简比,就是根据比的基本性质,把一个比化成最简整数比。
(1)32 ∶40前项32和后项40的最大公因数是8,所以根据比的基本性质,把32 ∶40的前项后项同时除以8,得到4 ∶5。这时,前项后项是只有公因数1的整数,32 ∶40化成最简比是4 ∶5。
(2)1.25 ∶ 2.5前项、后项都是小数,首先可以把它们都转化成整数,前项、后项同时乘100,原来的比就转化为125 ∶250,再根据化简整数比的方法,前项、后项同时除以125,得到1 ∶2。
(3) ∶前项、后项都是分数,同样要把它们转化为整数,前项、后项同时乘分母3和5的最小公倍数15,得到10 ∶3。
答案:(1)32 ∶40
=(32÷8) ∶(40÷8)
=4 ∶5
(2)1.25 ∶2.5
=(1.25×100) ∶(2.5×100)
=125 ∶250
=(125÷125) ∶(250÷125)
=1 ∶2
(3) ∶
= ∶
=10 ∶3
4. ∶化成最简单的整数比是( ) ∶( ), ∶8的比值是( )。
5. 把25 kg:0.25 t化成最简单的整数比是
( ) ∶( ),比值是( )。
9
10
0.05
1
10
6. 化简下面各比:
60 ∶32 0.45 ∶0.2
∶ 0.625 ∶
15 ∶8
9 ∶4
18 ∶35
5 ∶3
考点3:比例关系的判定
分别说明下面三种量中,当其中一种量一定时,其他两种量的比例关系。
(1)大米的总千克数一定,每天吃的千克数和天数;
(2)每天吃的千克数一定,大米的总千克数和天数;
(3)大米的总千克数一定,吃了的数量和剩余的数量。
方法指导:我们可以根据数量关系来判断。
(1)因为每天吃的千克数和天数是两种相关联的量,每天吃的千克数 × 天数 = 大米的总千克数(一定),所以大米的总千克数一定时,每天吃的千克数和天数成反比例。
(2)因为大米的总千克数和天数是两种相关联的量,
= 每天吃的千克数(一定),所以每天吃的千克数一定时,大米的总千克数和天数成正比例。
(3)吃了的数量和剩余的数量是两种相关联的量,它们的和一定,但是这两种量的乘积或者比值都不是一定的,所以吃了的数量和剩余的数量不成比例。
答案:(1)反比例关系。 (2)正比例关系。
(3)不成比例关系。
纸的总页数
每本的页数
本数
纸的总页数
每本的页数
本数
反
7. 用一批纸装订练习本,每本25页,可以装订400本。如果要装订500本,每本有x页。
题中( )一定,关系式:( ) ( )=( )(一定),
( )和( )成( )比例。
×
8. 在圆柱的侧面积、底面周长、高这三种量中,
当底面周长一定时,( )与( )成( )比例;
当高一定时,( )与( )成( )比例;
当侧面积一定时,( )与( )成( )比例。
侧面积
高
正
侧面积
底面周长
正
底面周长
高
反
9. 判断题。(正确的在括号里画“√”,错误的画“×”)
(1)工作总量一定,工作效率和工作时间成反比例。( )
(2)圆的周长和它的直径成正比例。( )
(3)分数的大小一定,它的分子和分母成反比例。( )
√
√
×
(4)在一定的距离内,车轮周长和它转动的圈数成反比例。( )
(5)在400 m赛跑中,跑步的速度和所用时间成反比例。( )
(6)被除数一定,除数和商成正比例。( )
√
√
×
小考真题演练
一填空题。
1. 男生占全班人数的,这个班男、女生人数的比
是( )。
2. 甲数的等于乙数的,甲数与乙数的比是( )。
3. 4 ∶5 = 24÷( )=( ) ∶15=
( )%。
5 ∶4
3 ∶5
30
12
80
4. 一种盐水是由盐和水按1 ∶30 的重量比配制而成的。其中,盐的重量占盐水的( ),水的重量占盐水的( )。
5. 如果x÷y =712×2,那么x和y成( )比例;如果x ∶4=5 ∶y,那么x和y成( )比例。
正
反
二 选择题。(将正确答案的字母编号填在括号里)
1. 小正方形和大正方形边长的比是2 ∶7,小正方形和大正方形面积的比是( )。
A. 2 ∶7 B. 6 ∶21
C. 4 ∶49 D. 7 ∶5
C
2. 与 ∶能组成比例的是( )。
A. ∶ B. ∶5
C. 5 ∶6 D. 6 ∶5
D
3. 小明从家里去学校,所需时间与行走的速度( )。
A. 成正比例 B. 成反比例
C. 不成比例 D. 以上都不对
B
4. 一件工作,甲单独做12天完成,乙单独做18天完成。甲、乙效率的最简比是( )。
A. 6 ∶9 B. 3 ∶2
C. 2 ∶3 D. 9 ∶6
5. 一个三角形三个内角度数的比是6 ∶2 ∶1,这个三角形是( )。
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 无法确定
B
C
三 计算。
1. 求比值。
∶0.75 ∶
0.25 ∶0.5
4
0.5
2. 化简比。
150 ∶30 2.6 ∶0.04 ∶
5 ∶1
65 ∶1
1 ∶16
3. 解比例。
25 ∶7=x ∶35 2.8 ∶0.8=0.7 ∶x
24 ∶ x=12 ∶ 14
x=125
x=0.2
x=28
∶= ∶x =
3 ∶12= ∶x
x=
x=0.4
x=3
四 根据下面的条件列出比例,并解比例。
1.96和x的比等于16和5的比。
96 ∶x=16 ∶5
x=30
2. 两个外项是24和18,两个内项是x和36。
24 ∶x=36 ∶18
x=12
五 解决问题。
1. 一种药水是用药粉和水按3 ∶400的重量比配制成的。
(1)要配制这种药水1612 kg,需要药粉多少千克?
1612×=12(kg)
答:需要药粉12 kg。
(2)用水60 kg,需要药粉多少千克?
60×=0.45(kg)
答:需要药粉0.45 kg。
(3)用48 kg药粉,可配制成多少千克的药水?
48÷+3=6448(kg)
答:可配制成6448 kg药水。
2. 一个晒盐场用500 kg海水可以晒15 kg盐;照这样的计算,用100 t海水可以晒多少吨盐?(用比例方法解答)
解:设用100 t海水可以晒x t盐。
15 ∶500=x ∶100
x=3
答:用100 t海水可以晒3 t盐。
2
0
2
2
2022年小升初数学复习
全国通用版
专题四 比和比例
第8课时 比和比例(包含正比例和反比例)
考点知识梳理
热门考点精讲
目录
小考真题演练
考点知识梳理
1. 比
(1)比的意义
两个数相除又叫做两个数的比。
(2)比的读法、写法和各部分的名称
在一个比中,“:”是比号,读作“比”。比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
(3)比与分数、除法之间的关系
名称 除法 分数 比
各部分名称 a ÷ b 被 除 除 除 号 数 数 a—分子 — —分数线 b——分母 a : b
前 比 后
项 号 项
区别 表示一种运算 表示一个数 表示两个量的倍比
(4)比的基本性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
(5)求比值和化简比
①最简整数比:比的前项和后项都是整数,并且其公因数只有1,这样的比就是最简整数比。
②求比值的方法:用比的前项除以后项所得的商,它的结果是一个数值,这个数值可以是整数,也可以是小数或分数。
③化简比:根据比的基本性质可以把比化成最简整数比,即比的前、后项是互质的数。
(6)比的应用
按比例分配问题:把一个数量按照一定的比分配成几部分,求每部分数量各是多少的问题叫做按比例分配问题。
方法:首先求出各部分占总量的几分之几,然后求出总量的几分之几是多少。
2. 比例
(1) 比例的意义
表示两个比相等的式子叫做比例。组成比例的四个数,叫做比例的项。两端的两项叫做外项,中间的两项叫做内项。
(2)比例的基本性质
在比例里,两个外项的积等于两个内向的积,这叫做比例的基本性质。
(3)解比例
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
(4)正比例和反比例
① 成正比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。用字母表示为=k(一定)。
②成反比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用字母表示为xy=k(一定)。
③判断正、反比例的方法
判断正、反比例可总结为“一找、二看、三判断”,如下。
找变量:分析数量关系,确定哪两种量是相关联的量。
看定量:分析这两种相关联的量,它们之间的关系是商一定还是积一定。
判断:如果商一定,就成正比例;如果积一定,就成反比例;如果商和积都不是定量,就不成比例。
④正、反比例的区别与联系
名称 不同点 相同点
意义不同 变化方向不同 关系式不同 正比例 两种相关联量中,相对应的两个数的比值,也就是商一定 一种量扩大(或缩小),另一种量也随之扩大(或缩小) =k(一定) 两种相关联的量,一种量变化,另一种量也随之变化
反比例 两种相关联量中,相对应的两个数的乘积一定 一种量扩大(或缩小),另一种量反而随之缩小(或扩大) xy=k(一定) 3. 比和比例的区别与联系
名称 比 比例
意义 表示两数相除 表示两个比相等的式子
各部分 名称 5 ∶ 8 前 比 后 项 号 项 10 ∶ 16 = 5 ∶8
外 内 内 外
项 项 项 项
基本性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变 在比例里,两个外项的积等于两个内项的积
化简比的依据 解比例的依据
热门考点精讲
考点1:写出两个量的比
写出两个量的比。
(1)甲仓库的与乙仓库的相等,甲、乙两个仓库的存粮的比是( )。
(2)从甲地走向乙地,小亮走完需要12分钟,小明走完需要8分钟。小亮和小明所用时间的比是( ),他们的速度比是( )。
方法指导:此题考查比的意义。(1)假设甲仓库的与乙仓库的都是1,可用除法求出甲、乙两个仓库的存粮,进而作比即可。(2)根据路程、时间、速度的关系,求出各自的速度,再利用比的性质化简比。
答案:(1)4 ∶5 (2)3 ∶22 ∶3
1. 已知A是B的2.4倍,那么A ∶B=( ) ∶( )。
2. 一项工程,甲单独做要10天完成,乙单独做要12天完成,甲、乙的工作效率比是( ) ∶( )。
12
5
6
5
3. 已知小圆的半径是2 cm,大圆的半径是3 cm,小圆和大圆的周长比是( ) ∶( ),面积比是( ) ∶( )。
易错点拨:写两数的比时,没有写成最简整数比。
2
3
4
9
考点2:化简比
化简下列各比:
(1)32 ∶40
(2)1.25 ∶ 2.5
(3) ∶
方法指导:化简比,就是根据比的基本性质,把一个比化成最简整数比。
(1)32 ∶40前项32和后项40的最大公因数是8,所以根据比的基本性质,把32 ∶40的前项后项同时除以8,得到4 ∶5。这时,前项后项是只有公因数1的整数,32 ∶40化成最简比是4 ∶5。
(2)1.25 ∶ 2.5前项、后项都是小数,首先可以把它们都转化成整数,前项、后项同时乘100,原来的比就转化为125 ∶250,再根据化简整数比的方法,前项、后项同时除以125,得到1 ∶2。
(3) ∶前项、后项都是分数,同样要把它们转化为整数,前项、后项同时乘分母3和5的最小公倍数15,得到10 ∶3。
答案:(1)32 ∶40
=(32÷8) ∶(40÷8)
=4 ∶5
(2)1.25 ∶2.5
=(1.25×100) ∶(2.5×100)
=125 ∶250
=(125÷125) ∶(250÷125)
=1 ∶2
(3) ∶
= ∶
=10 ∶3
4. ∶化成最简单的整数比是( ) ∶( ), ∶8的比值是( )。
5. 把25 kg:0.25 t化成最简单的整数比是
( ) ∶( ),比值是( )。
9
10
0.05
1
10
6. 化简下面各比:
60 ∶32 0.45 ∶0.2
∶ 0.625 ∶
15 ∶8
9 ∶4
18 ∶35
5 ∶3
考点3:比例关系的判定
分别说明下面三种量中,当其中一种量一定时,其他两种量的比例关系。
(1)大米的总千克数一定,每天吃的千克数和天数;
(2)每天吃的千克数一定,大米的总千克数和天数;
(3)大米的总千克数一定,吃了的数量和剩余的数量。
方法指导:我们可以根据数量关系来判断。
(1)因为每天吃的千克数和天数是两种相关联的量,每天吃的千克数 × 天数 = 大米的总千克数(一定),所以大米的总千克数一定时,每天吃的千克数和天数成反比例。
(2)因为大米的总千克数和天数是两种相关联的量,
= 每天吃的千克数(一定),所以每天吃的千克数一定时,大米的总千克数和天数成正比例。
(3)吃了的数量和剩余的数量是两种相关联的量,它们的和一定,但是这两种量的乘积或者比值都不是一定的,所以吃了的数量和剩余的数量不成比例。
答案:(1)反比例关系。 (2)正比例关系。
(3)不成比例关系。
纸的总页数
每本的页数
本数
纸的总页数
每本的页数
本数
反
7. 用一批纸装订练习本,每本25页,可以装订400本。如果要装订500本,每本有x页。
题中( )一定,关系式:( ) ( )=( )(一定),
( )和( )成( )比例。
×
8. 在圆柱的侧面积、底面周长、高这三种量中,
当底面周长一定时,( )与( )成( )比例;
当高一定时,( )与( )成( )比例;
当侧面积一定时,( )与( )成( )比例。
侧面积
高
正
侧面积
底面周长
正
底面周长
高
反
9. 判断题。(正确的在括号里画“√”,错误的画“×”)
(1)工作总量一定,工作效率和工作时间成反比例。( )
(2)圆的周长和它的直径成正比例。( )
(3)分数的大小一定,它的分子和分母成反比例。( )
√
√
×
(4)在一定的距离内,车轮周长和它转动的圈数成反比例。( )
(5)在400 m赛跑中,跑步的速度和所用时间成反比例。( )
(6)被除数一定,除数和商成正比例。( )
√
√
×
小考真题演练
一填空题。
1. 男生占全班人数的,这个班男、女生人数的比
是( )。
2. 甲数的等于乙数的,甲数与乙数的比是( )。
3. 4 ∶5 = 24÷( )=( ) ∶15=
( )%。
5 ∶4
3 ∶5
30
12
80
4. 一种盐水是由盐和水按1 ∶30 的重量比配制而成的。其中,盐的重量占盐水的( ),水的重量占盐水的( )。
5. 如果x÷y =712×2,那么x和y成( )比例;如果x ∶4=5 ∶y,那么x和y成( )比例。
正
反
二 选择题。(将正确答案的字母编号填在括号里)
1. 小正方形和大正方形边长的比是2 ∶7,小正方形和大正方形面积的比是( )。
A. 2 ∶7 B. 6 ∶21
C. 4 ∶49 D. 7 ∶5
C
2. 与 ∶能组成比例的是( )。
A. ∶ B. ∶5
C. 5 ∶6 D. 6 ∶5
D
3. 小明从家里去学校,所需时间与行走的速度( )。
A. 成正比例 B. 成反比例
C. 不成比例 D. 以上都不对
B
4. 一件工作,甲单独做12天完成,乙单独做18天完成。甲、乙效率的最简比是( )。
A. 6 ∶9 B. 3 ∶2
C. 2 ∶3 D. 9 ∶6
5. 一个三角形三个内角度数的比是6 ∶2 ∶1,这个三角形是( )。
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 无法确定
B
C
三 计算。
1. 求比值。
∶0.75 ∶
0.25 ∶0.5
4
0.5
2. 化简比。
150 ∶30 2.6 ∶0.04 ∶
5 ∶1
65 ∶1
1 ∶16
3. 解比例。
25 ∶7=x ∶35 2.8 ∶0.8=0.7 ∶x
24 ∶ x=12 ∶ 14
x=125
x=0.2
x=28
∶= ∶x =
3 ∶12= ∶x
x=
x=0.4
x=3
四 根据下面的条件列出比例,并解比例。
1.96和x的比等于16和5的比。
96 ∶x=16 ∶5
x=30
2. 两个外项是24和18,两个内项是x和36。
24 ∶x=36 ∶18
x=12
五 解决问题。
1. 一种药水是用药粉和水按3 ∶400的重量比配制成的。
(1)要配制这种药水1612 kg,需要药粉多少千克?
1612×=12(kg)
答:需要药粉12 kg。
(2)用水60 kg,需要药粉多少千克?
60×=0.45(kg)
答:需要药粉0.45 kg。
(3)用48 kg药粉,可配制成多少千克的药水?
48÷+3=6448(kg)
答:可配制成6448 kg药水。
2. 一个晒盐场用500 kg海水可以晒15 kg盐;照这样的计算,用100 t海水可以晒多少吨盐?(用比例方法解答)
解:设用100 t海水可以晒x t盐。
15 ∶500=x ∶100
x=3
答:用100 t海水可以晒3 t盐。
同课章节目录
