2022年小升初数学总复习(通用版) 第12课时 平面图形的认识与测量课件(69张PPT)
文档属性
| 名称 | 2022年小升初数学总复习(通用版) 第12课时 平面图形的认识与测量课件(69张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 16:12:28 | ||
图片预览







文档简介
(共69张PPT)
2
0
2
2
2022年小升初数学复习
全国通用版
专题六 图形的认识与测量
第12课时 平面图形的认识与测量
考点知识梳理
热门考点精讲
目录
小考真题演练
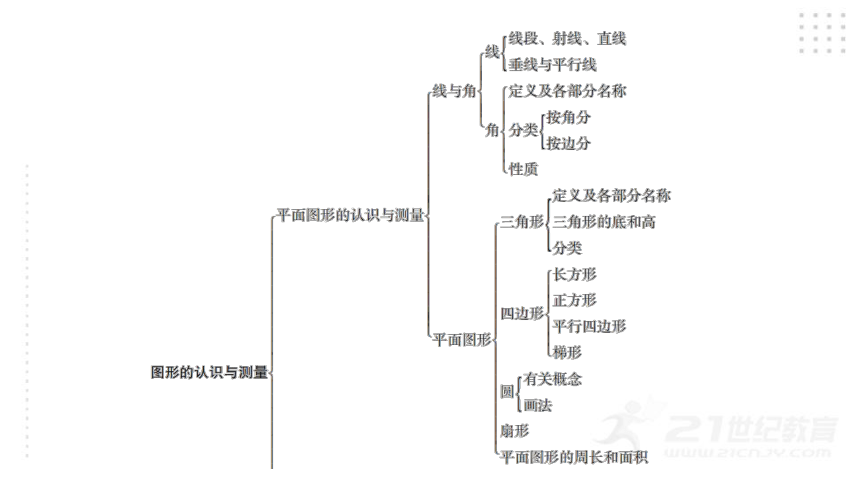
考点知识梳理
一、线与角
1. 线
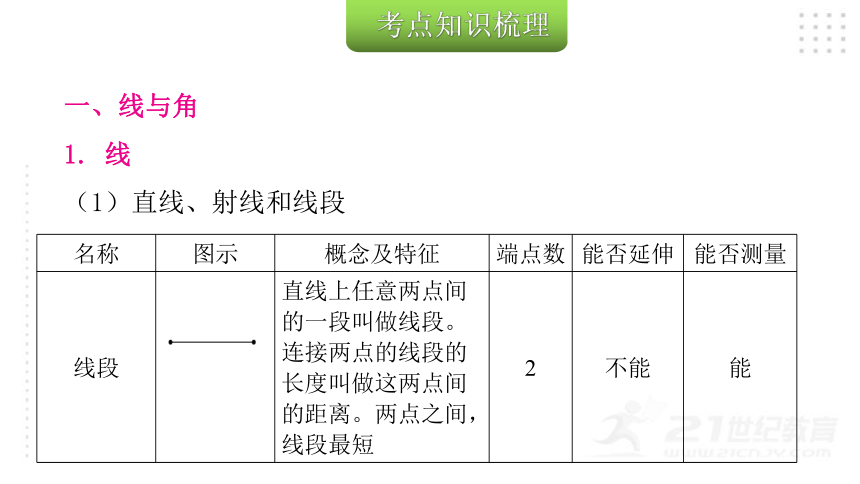
(1)直线、射线和线段
名称 图示 概念及特征 端点数 能否延伸 能否测量
线段 直线上任意两点间的一段叫做线段。 连接两点的线段的长度叫做这两点间的距离。两点之间,线段最短 2 不能 能
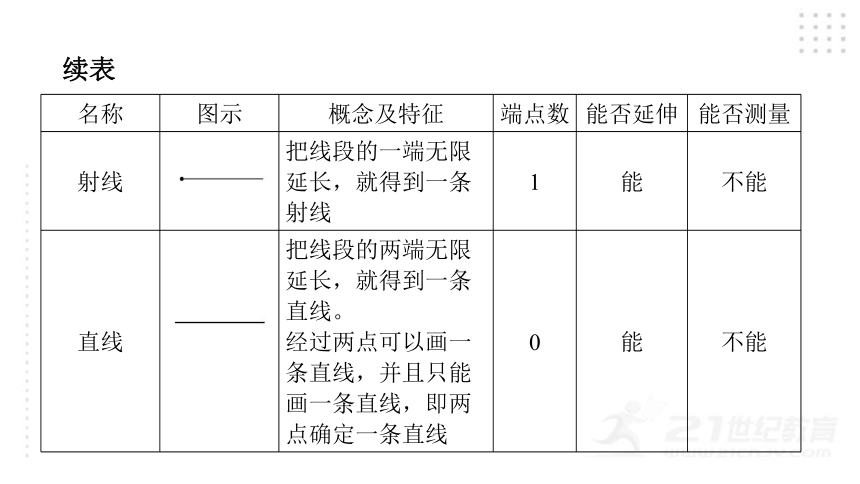
名称 图示 概念及特征 端点数 能否延伸 能否测量
射线 把线段的一端无限延长,就得到一条射线 1 能 不能
直线 把线段的两端无限延长,就得到一条直线。 经过两点可以画一条直线,并且只能画一条直线,即两点确定一条直线 0 能 不能
续表
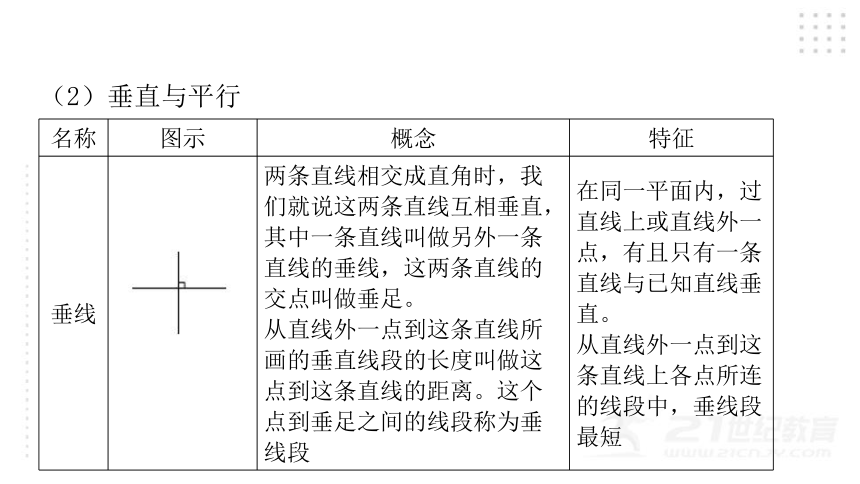
(2)垂直与平行
名称 图示 概念 特征
垂线 两条直线相交成直角时,我们就说这两条直线互相垂直,其中一条直线叫做另外一条直线的垂线,这两条直线的交点叫做垂足。 从直线外一点到这条直线所画的垂直线段的长度叫做这点到这条直线的距离。这个点到垂足之间的线段称为垂线段 在同一平面内,过直线上或直线外一点,有且只有一条直线与已知直线垂直。
从直线外一点到这条直线上各点所连的线段中,垂线段最短
名称 图示 概念 特征
平行线 同一平面内不相交的两条直线互相平行,其中一条直线是另外一条直线的平行线。 两直线平行时,从一条直线上任意一点向另一条直线作垂线,所得的平行线间的垂直线段的长度,叫做平行线间的距离 平行线之间的距离处处相等
续表
温馨提示:在同一平面内的两条不重合的直线,只有两种位置关系——相交和平行,不包括垂直,因为垂直是相交的一种特殊情况。
2. 角
(1)角的定义:从一点引出的两条射线所组成的图形叫做角。
(2)角各部分的名称:如右图,图中的点是角的顶点,两条射线是角的边。角通常用符号“∠”来表示。图中的角记作∠1,读作角1。
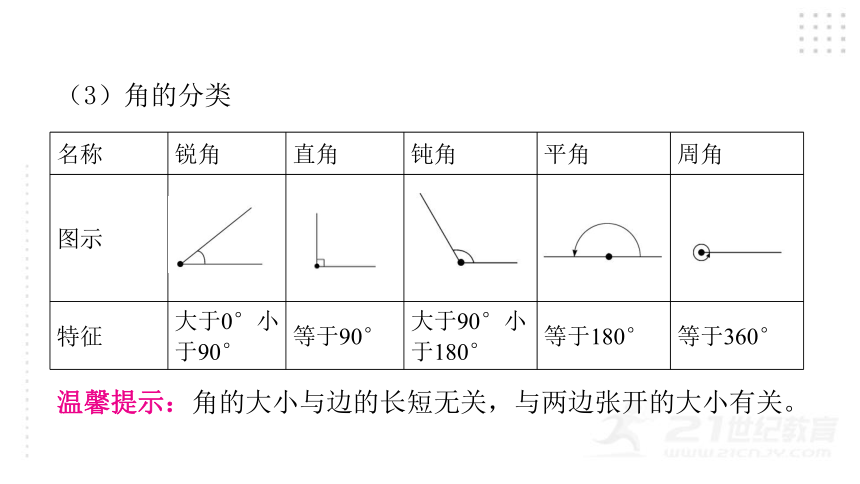
(3)角的分类
名称 锐角 直角 钝角 平角 周角
图示
特征 大于0°小于90° 等于90° 大于90°小于180° 等于180° 等于360°
温馨提示:角的大小与边的长短无关,与两边张开的大小有关。
二、平面图形
1. 三角形
(1)三角形的定义:在同一平面内,由不在同一条直线上的三条线段首尾顺次相接所组成的封闭图形叫做三角形。
(2)三角形各部分的名称:如下图所示,围成三角形的三条线段叫做三角形的三条边;三角形每两
条边的交点叫做三角形的顶点;三角形
相邻两边所组成的角,叫做三角形的内角。
(3)三角形的底和高:从三角形任一顶点向它的对边或对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高。这个顶点所对的边叫做三角形的底。
温馨提示:每个三角形都有三个底和对应的高。
(4)三角形的分类
①按角分
名称 锐角三角形 直角三角形 钝角三角形
图形
特征 三个角都是锐角 有一个角是直角, 另外两个角是锐角 有一个角是钝角,
另外两个角是锐角
②按边分
名称 不等边三角形 等腰三角形 等边三角形
图形
特征 三条边都不相等 其中两条边相等, 第三条边不相等 三条边都相等
(5)三角形的性质
①三角形具有稳定性。
②三角形的内角和是180°。
③三角形任意两边的和大于第三边。
2. 四边形
(1)四边形的分类及其特点
名称 图形 特征
长方形 两组对边分别
平行且相等,
四个角都是直角
平行四边形 两组对边分别
平行且相等,
对角相等
名称 图形 特征
正方形 四条边都相等,
四个角都是直角
梯形 只有一组
对边平行
续表
(2)梯形的两种特殊形式及其特征
名称 图形 特征
等腰梯形 两腰相等,两底角相等
直角梯形 有两个角是直角,一条腰与两底边垂直
(3)四边形的分类及其关系,如下图所示:
温馨提示:平行四边形容易变形,具有不稳定性。平行四边形有无数条高。
3. 圆
(1)圆的认识:平面上的一种曲线图形。圆中心的一点叫做圆心,一般用字母O表示。
①半径:连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。
②直径:通过圆心,两端都在圆上的线段叫做直径,一般用字母d表示。
③圆心决定圆的位置,半径决定圆的大小,直径是圆内最长的线段。
④在同一个圆里,有无数条半径,每条半径的长度都相等。
⑤在同一个圆里,有无数条直径,每条直径的长度都相等。
⑥在同一个圆里,直径等于半径长度的两倍,即d=2r,或r=。
⑦直径所在的直线是圆的对称轴,圆有无数条对称轴。
(2)圆的画法:把圆规的两脚张开,张开的距离就是圆的半径;把有针尖的一只脚固定在一个点上,这个点的位置就是圆心;把装有铅笔的一只脚旋转一周,就画出一个圆了。
4. 扇形
(1)一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
(2)圆上A,B两点之间的部分叫做弧,读作“弧AB”,记作“ ”。
(3)顶点在圆心的角叫做圆心角。
(4)在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。以半圆为弧的扇形的圆心角是180°,以圆为弧的扇形的圆心角是90°。
(5)扇形只有一条对称轴。
5. 平面图形的周长
周长:封闭图形一周的长度。
(1)长方形的周长=(长+宽)×2 C长=2(a+b)
=长×2+宽×2 C长=2a+2b
(2)正方形的周长=边长×4 C正=4a
正方形的边长=周长÷4 a=C正÷4
(3)圆的周长=直径×π C圆=πd
=2×半径×π C圆=2πr
圆的直径=圆的周长÷π d=C圆÷π
圆的半径=圆的周长÷π÷2 r=C圆÷π÷2
(4)半圆的周长=圆周长的一半+直径
C半圆=C÷2+d
6. 平面图形的面积
(1)长方形的面积=长×宽 S长=ab
(2)正方形的面积=边长×边长 S正=a2
(3)平行四边形的面积=底×高 S□=ah
(4)三角形的面积=×底×高 S△=ah
(5)梯形的面积=×(上底+下底)×高 S梯=(a+b)h
(6)圆的面积=半径的平方×π S圆=πr2
(7)圆环的面积=大圆面积-小圆面积
S环=S大圆-S小圆=π(R2-r2)
7. 平面图形之间的关系
(1)面积相等的平行四边形和三角形,当它们等底时,三角形的高是平行四边形高的2倍;当它们等高时,三角形的底是平行四边形底的2倍。
(2)长方形的周长总和一定时,长和宽越接近,长方形的面积就越大,当长和宽相等时面积最大。
(注意:在计算与圆相关的面积和表面积时,把π放到最后再计算,能让计算更加简便,并提高正确率。)
热门考点精讲
考点1:直线、射线和线段的特征
图中有( )条直线,( )条线段,( )条射线。
方法指导:本题主要考查直线、线段和射线的认识,关键是根据直线、射线和线段的定义和特征来解题。
答案:1 1 4
1. 过一点可以画( )直线,从一点出发,可以画( )射线。
2. ( )、( )都没有长度,其中
( )没有端点,( )只有一个端点。
3. 下图中有( )条线段,( )条射线。
无数条
无数条
直线
射线
直线
射线
3
6
考点2:垂线(高)的画法
画一画。
(1)过P点作AB的垂线;
(2)画出下面各图AB边上的高。
方法指导:画垂线的方法为用三角尺一条边与已知直线重合,然后沿着直线移动三角尺,让P点和三角尺的另外一条直角边重合,过P点沿直角边画直线。画高的方法和画垂线的方法相同,不过要注意高的垂足应该在AB边上,并标出垂足。
答案:
4. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
5. 在同一平面内画一条已知直线的垂线,可以画( )条;如果是过一点画已知直线的垂线,可以画( )条。
垂直
无数
1
6. 过点Q作直线AB的垂线。
7. 请你设计一条从稻田到小河最近的管道。
考点3:求角的大小
已知∠1=68°,那么∠2=( )°,∠3=( )°,∠4=( )°。
方法指导:利用平角=180°以及图中各角之间的关系可以知道,∠2=180°-∠1=180°-68°=112°,同理∠3=180°-∠2=180°-112°=68°,∠4=180°-∠1=180°-68°=112°;或者根据两条直线相交,相对的两个角相等,所以∠1=∠3=68°,∠2=∠4=112°。
答案:112 68 112
8. 在直角三角形中,∠A=53°,∠B=( )°。
37
9. 如下图,∠1=( )°,∠2=( )°,∠3=( )°。
90
60
140
考点4:三角形的有关计算
三角形三个角的度数比是1 ∶1 ∶2,这个三角形是( )三角形。
方法指导:此题考查三角形的分类,根据比的知识求出每个角的度数,其中占1份的两个角都是180°×=180°×=45°,
180°-45°-45°=90°。有一个角是90°的三角形是直角三角形,有两个角相等的三角形是等腰三角形,所以这个三角形是等腰直角三角形。还可以直接通过比看出,两个占1份的角是相等的,占2份的角正好是一半就是90°,也能得到等腰直角三角形。
答案:等腰直角
10. 如果一个三角形三个角的比是1 ∶2 ∶3,那么这个三角形是( )三角形。
11. 如下图,一个等腰三角形顶角的度数正好是两个底角度数和的2倍。这个三角形的三个内角各是多少度?
直角
180°÷(2×2+2)=30°
30°×4=120°
答:这个三角形的三个内角各是30°,30°,120°。
考点5:四边形的有关计算
已知平行四边形的周长是38 cm,其中一条边长是10 cm,与它相邻的一条边长是多少厘米?
方法指导:根据平行四边形的特点,对边相等可得平行四边形的周长的求解方法与长方形相似,都是相邻两条边的和的2倍,由此先用周长38 cm除以2,求出相邻两边的和,再减去其中的一条边10 cm,即可求出另一条边。
答案:38÷2-10=9(cm)
答:与它相邻的一条边长是9 cm。
12. 长方形的对边( ),正方形的四个角都是( )。
13. 一个长方形的周长是90 cm,长与宽的长度之比是5 ∶4,这个长方形的长和宽各是多少厘米?
平行且相等
直角
90÷2÷(4+5)=5(cm)
长:5×5=25(cm) 宽:4×5=20(cm)
答:这个长方形的长是25 cm,宽是20 cm。
考点6:圆的有关计算
已知线段AB的长度是45 cm。
(1)小圆的半径是多少厘米?
(2)大圆的直径是多少厘米?
方法指导:(1)根据图意可知,大圆的半径等于小圆的直径,也就是大圆的半径等于小圆半径的2倍,所以线段AB的长度等于OB长度的2+1=3倍,据此计算可求出小圆的半径。
(2)用小圆半径乘2求出小圆直径,也就是大圆半径,再乘2就是大圆直径,据此列式计算即可解答。
答案:(1)45÷(2+1)=15(cm)
答:小圆的半径是15 cm。
(2)15×2×2=60(cm)
答:大圆的直径是60 cm。
14. 圆有( )个圆心,( )条半径,半径决定圆的( )。
1
无数
大小
15. 王明要在一个长7 cm,宽4 cm的长方形中画一个最大的圆,这个圆的直径是多少?面积是多少?
解:长方形内最大的圆的直径等于长方形的宽,是4 cm,
圆的半径:4÷2=2(cm)
圆的面积:3.14×22=12.56(cm2)
答:这个圆的直径是4 cm,面积是12.56 cm2。
易错点拨:对图形不够了解。
小考真题演练
一 填空题。
1. 三角形按角分类,可以分为( )、
( )、( );按边分类,可以分为( )、( )、
( )。
2. ( )决定圆的位置,( )决定圆的大小。
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
圆心
半径
3. 在同一平面上,过直线外一点,能画已知直线的垂线共( )条,能画已知直线的平行线共( )条。
4. 过一点能画( )条直线,过两点能画( )条直线。
5. 等腰三角形的一个角是45°,另外两个角可能是( )°和( )°或( )°和( )°。
1
1
无数
1
45
90
67.5
67.5
6. 只有一组对边平行,其中一个角是90°的四边形
是( )。
7. ( )具有不稳定性,伸缩门就是应用了这个特性。
8. 把一个长6 cm,宽4 cm的长方形剪成最大的正方形,这个正方形的周长是( )cm,面积是( )cm2。
直角梯形
平行四边形
16
16
9. 一个三角形的面积是12 cm2,和它等底等高的平行四边形的面积是( )cm2。
10. 一个直角三角形的三条边分别是3 cm,4 cm,5 cm,这个三角形的面积是( )cm2,斜边上的高是( )cm。
24
6
2.4
二 选择题。(将正确答案的字母编号填在括号里)
1. ( )具有稳定性,( )具有不稳定性。
A. 三角形 B. 四边形
C. 三角形和四边形
A
B
2. 圆的半径和直径都是一条( ),圆的对称轴是一条( )。
A. 直线 B. 射线 C. 线段
3. 下列选项中,不正确的是( )。
A. 把线段的一端无限延伸,就得到一条射线
B. 大于90°的角是钝角
C. 三角形的内角和是180°
C
A
B
4. 把一个平行四边形拉成长方形,周长( ),面积( )。
A. 不变 B. 变大 C. 变小
5.下图中a,b是两条平行线,三个涂色部分图形的面积相比,( )最大。
A. 平行四边形
B. 三角形
C. 梯形
A
B
A
三 判断题。(正确的在括号里画“√”,错误的画“×”)
1. 延长角的两条边,角就变大了。( )
2. 任意三条线段都能围成一个三角形。( )
3. 正方形是特殊的长方形,长方形是特殊的平行四边形。( )
4. 圆有无数条对称轴。( )
5. 等腰梯形只有一组对边平行,且只有两条边相等。( )
×
×
√
√
×
四 操作题。
1. 量出下面各角的度数。
(1)112°
(2)25°
(3)68°
2. 画并测量从Q点到直线AB的距离。
距离是2 cm。
3. 画出下列图形中底边上的高。
五 按要求计算。(单位:cm)
1. 计算图形的面积。
8×8+8×8×=96(cm2)
2. 计算图形的周长。
4×4=16(cm)
3. 计算阴影部分的面积。
8÷2=4(cm)
8×4-3.14×42÷2=32-25.12=6.88(cm2)
六 解决问题。
1. 已知右图中∠1=35°,∠2=30°,列算式求出其他各角的度数。
∠3=90°-∠2=90°-30°=60°
∠4=90°-∠1=90°-35°=55°
∠5=180°-∠1=180°-35°=145°
∠6=180°-∠5=180°-145°=35°
2. 曲米有两根同样长的小棒,长5 dm,如果她想用三根小棒摆成一个三角形,第3根小棒最长是多少分米(取整分米数)?曲婷给了她一根小棒,结果摆成的三角形的一个底角是35°。顶角是多少度?
第3根小棒<5+5=10(dm)
180°-35°×2=110°
答:第3根小棒最长是9 dm。顶角是110°。
3. 刘大伯用36 m长的篱笆靠墙围了一个鸡圈(如图),这个鸡圈的占地面积是多少平方米?
(36-10)×10÷2=130(m2)
答:这个鸡圈的占地面积是130 m2。
2
0
2
2
2022年小升初数学复习
全国通用版
专题六 图形的认识与测量
第12课时 平面图形的认识与测量
考点知识梳理
热门考点精讲
目录
小考真题演练
考点知识梳理
一、线与角
1. 线
(1)直线、射线和线段
名称 图示 概念及特征 端点数 能否延伸 能否测量
线段 直线上任意两点间的一段叫做线段。 连接两点的线段的长度叫做这两点间的距离。两点之间,线段最短 2 不能 能
名称 图示 概念及特征 端点数 能否延伸 能否测量
射线 把线段的一端无限延长,就得到一条射线 1 能 不能
直线 把线段的两端无限延长,就得到一条直线。 经过两点可以画一条直线,并且只能画一条直线,即两点确定一条直线 0 能 不能
续表
(2)垂直与平行
名称 图示 概念 特征
垂线 两条直线相交成直角时,我们就说这两条直线互相垂直,其中一条直线叫做另外一条直线的垂线,这两条直线的交点叫做垂足。 从直线外一点到这条直线所画的垂直线段的长度叫做这点到这条直线的距离。这个点到垂足之间的线段称为垂线段 在同一平面内,过直线上或直线外一点,有且只有一条直线与已知直线垂直。
从直线外一点到这条直线上各点所连的线段中,垂线段最短
名称 图示 概念 特征
平行线 同一平面内不相交的两条直线互相平行,其中一条直线是另外一条直线的平行线。 两直线平行时,从一条直线上任意一点向另一条直线作垂线,所得的平行线间的垂直线段的长度,叫做平行线间的距离 平行线之间的距离处处相等
续表
温馨提示:在同一平面内的两条不重合的直线,只有两种位置关系——相交和平行,不包括垂直,因为垂直是相交的一种特殊情况。
2. 角
(1)角的定义:从一点引出的两条射线所组成的图形叫做角。
(2)角各部分的名称:如右图,图中的点是角的顶点,两条射线是角的边。角通常用符号“∠”来表示。图中的角记作∠1,读作角1。
(3)角的分类
名称 锐角 直角 钝角 平角 周角
图示
特征 大于0°小于90° 等于90° 大于90°小于180° 等于180° 等于360°
温馨提示:角的大小与边的长短无关,与两边张开的大小有关。
二、平面图形
1. 三角形
(1)三角形的定义:在同一平面内,由不在同一条直线上的三条线段首尾顺次相接所组成的封闭图形叫做三角形。
(2)三角形各部分的名称:如下图所示,围成三角形的三条线段叫做三角形的三条边;三角形每两
条边的交点叫做三角形的顶点;三角形
相邻两边所组成的角,叫做三角形的内角。
(3)三角形的底和高:从三角形任一顶点向它的对边或对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高。这个顶点所对的边叫做三角形的底。
温馨提示:每个三角形都有三个底和对应的高。
(4)三角形的分类
①按角分
名称 锐角三角形 直角三角形 钝角三角形
图形
特征 三个角都是锐角 有一个角是直角, 另外两个角是锐角 有一个角是钝角,
另外两个角是锐角
②按边分
名称 不等边三角形 等腰三角形 等边三角形
图形
特征 三条边都不相等 其中两条边相等, 第三条边不相等 三条边都相等
(5)三角形的性质
①三角形具有稳定性。
②三角形的内角和是180°。
③三角形任意两边的和大于第三边。
2. 四边形
(1)四边形的分类及其特点
名称 图形 特征
长方形 两组对边分别
平行且相等,
四个角都是直角
平行四边形 两组对边分别
平行且相等,
对角相等
名称 图形 特征
正方形 四条边都相等,
四个角都是直角
梯形 只有一组
对边平行
续表
(2)梯形的两种特殊形式及其特征
名称 图形 特征
等腰梯形 两腰相等,两底角相等
直角梯形 有两个角是直角,一条腰与两底边垂直
(3)四边形的分类及其关系,如下图所示:
温馨提示:平行四边形容易变形,具有不稳定性。平行四边形有无数条高。
3. 圆
(1)圆的认识:平面上的一种曲线图形。圆中心的一点叫做圆心,一般用字母O表示。
①半径:连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。
②直径:通过圆心,两端都在圆上的线段叫做直径,一般用字母d表示。
③圆心决定圆的位置,半径决定圆的大小,直径是圆内最长的线段。
④在同一个圆里,有无数条半径,每条半径的长度都相等。
⑤在同一个圆里,有无数条直径,每条直径的长度都相等。
⑥在同一个圆里,直径等于半径长度的两倍,即d=2r,或r=。
⑦直径所在的直线是圆的对称轴,圆有无数条对称轴。
(2)圆的画法:把圆规的两脚张开,张开的距离就是圆的半径;把有针尖的一只脚固定在一个点上,这个点的位置就是圆心;把装有铅笔的一只脚旋转一周,就画出一个圆了。
4. 扇形
(1)一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
(2)圆上A,B两点之间的部分叫做弧,读作“弧AB”,记作“ ”。
(3)顶点在圆心的角叫做圆心角。
(4)在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。以半圆为弧的扇形的圆心角是180°,以圆为弧的扇形的圆心角是90°。
(5)扇形只有一条对称轴。
5. 平面图形的周长
周长:封闭图形一周的长度。
(1)长方形的周长=(长+宽)×2 C长=2(a+b)
=长×2+宽×2 C长=2a+2b
(2)正方形的周长=边长×4 C正=4a
正方形的边长=周长÷4 a=C正÷4
(3)圆的周长=直径×π C圆=πd
=2×半径×π C圆=2πr
圆的直径=圆的周长÷π d=C圆÷π
圆的半径=圆的周长÷π÷2 r=C圆÷π÷2
(4)半圆的周长=圆周长的一半+直径
C半圆=C÷2+d
6. 平面图形的面积
(1)长方形的面积=长×宽 S长=ab
(2)正方形的面积=边长×边长 S正=a2
(3)平行四边形的面积=底×高 S□=ah
(4)三角形的面积=×底×高 S△=ah
(5)梯形的面积=×(上底+下底)×高 S梯=(a+b)h
(6)圆的面积=半径的平方×π S圆=πr2
(7)圆环的面积=大圆面积-小圆面积
S环=S大圆-S小圆=π(R2-r2)
7. 平面图形之间的关系
(1)面积相等的平行四边形和三角形,当它们等底时,三角形的高是平行四边形高的2倍;当它们等高时,三角形的底是平行四边形底的2倍。
(2)长方形的周长总和一定时,长和宽越接近,长方形的面积就越大,当长和宽相等时面积最大。
(注意:在计算与圆相关的面积和表面积时,把π放到最后再计算,能让计算更加简便,并提高正确率。)
热门考点精讲
考点1:直线、射线和线段的特征
图中有( )条直线,( )条线段,( )条射线。
方法指导:本题主要考查直线、线段和射线的认识,关键是根据直线、射线和线段的定义和特征来解题。
答案:1 1 4
1. 过一点可以画( )直线,从一点出发,可以画( )射线。
2. ( )、( )都没有长度,其中
( )没有端点,( )只有一个端点。
3. 下图中有( )条线段,( )条射线。
无数条
无数条
直线
射线
直线
射线
3
6
考点2:垂线(高)的画法
画一画。
(1)过P点作AB的垂线;
(2)画出下面各图AB边上的高。
方法指导:画垂线的方法为用三角尺一条边与已知直线重合,然后沿着直线移动三角尺,让P点和三角尺的另外一条直角边重合,过P点沿直角边画直线。画高的方法和画垂线的方法相同,不过要注意高的垂足应该在AB边上,并标出垂足。
答案:
4. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
5. 在同一平面内画一条已知直线的垂线,可以画( )条;如果是过一点画已知直线的垂线,可以画( )条。
垂直
无数
1
6. 过点Q作直线AB的垂线。
7. 请你设计一条从稻田到小河最近的管道。
考点3:求角的大小
已知∠1=68°,那么∠2=( )°,∠3=( )°,∠4=( )°。
方法指导:利用平角=180°以及图中各角之间的关系可以知道,∠2=180°-∠1=180°-68°=112°,同理∠3=180°-∠2=180°-112°=68°,∠4=180°-∠1=180°-68°=112°;或者根据两条直线相交,相对的两个角相等,所以∠1=∠3=68°,∠2=∠4=112°。
答案:112 68 112
8. 在直角三角形中,∠A=53°,∠B=( )°。
37
9. 如下图,∠1=( )°,∠2=( )°,∠3=( )°。
90
60
140
考点4:三角形的有关计算
三角形三个角的度数比是1 ∶1 ∶2,这个三角形是( )三角形。
方法指导:此题考查三角形的分类,根据比的知识求出每个角的度数,其中占1份的两个角都是180°×=180°×=45°,
180°-45°-45°=90°。有一个角是90°的三角形是直角三角形,有两个角相等的三角形是等腰三角形,所以这个三角形是等腰直角三角形。还可以直接通过比看出,两个占1份的角是相等的,占2份的角正好是一半就是90°,也能得到等腰直角三角形。
答案:等腰直角
10. 如果一个三角形三个角的比是1 ∶2 ∶3,那么这个三角形是( )三角形。
11. 如下图,一个等腰三角形顶角的度数正好是两个底角度数和的2倍。这个三角形的三个内角各是多少度?
直角
180°÷(2×2+2)=30°
30°×4=120°
答:这个三角形的三个内角各是30°,30°,120°。
考点5:四边形的有关计算
已知平行四边形的周长是38 cm,其中一条边长是10 cm,与它相邻的一条边长是多少厘米?
方法指导:根据平行四边形的特点,对边相等可得平行四边形的周长的求解方法与长方形相似,都是相邻两条边的和的2倍,由此先用周长38 cm除以2,求出相邻两边的和,再减去其中的一条边10 cm,即可求出另一条边。
答案:38÷2-10=9(cm)
答:与它相邻的一条边长是9 cm。
12. 长方形的对边( ),正方形的四个角都是( )。
13. 一个长方形的周长是90 cm,长与宽的长度之比是5 ∶4,这个长方形的长和宽各是多少厘米?
平行且相等
直角
90÷2÷(4+5)=5(cm)
长:5×5=25(cm) 宽:4×5=20(cm)
答:这个长方形的长是25 cm,宽是20 cm。
考点6:圆的有关计算
已知线段AB的长度是45 cm。
(1)小圆的半径是多少厘米?
(2)大圆的直径是多少厘米?
方法指导:(1)根据图意可知,大圆的半径等于小圆的直径,也就是大圆的半径等于小圆半径的2倍,所以线段AB的长度等于OB长度的2+1=3倍,据此计算可求出小圆的半径。
(2)用小圆半径乘2求出小圆直径,也就是大圆半径,再乘2就是大圆直径,据此列式计算即可解答。
答案:(1)45÷(2+1)=15(cm)
答:小圆的半径是15 cm。
(2)15×2×2=60(cm)
答:大圆的直径是60 cm。
14. 圆有( )个圆心,( )条半径,半径决定圆的( )。
1
无数
大小
15. 王明要在一个长7 cm,宽4 cm的长方形中画一个最大的圆,这个圆的直径是多少?面积是多少?
解:长方形内最大的圆的直径等于长方形的宽,是4 cm,
圆的半径:4÷2=2(cm)
圆的面积:3.14×22=12.56(cm2)
答:这个圆的直径是4 cm,面积是12.56 cm2。
易错点拨:对图形不够了解。
小考真题演练
一 填空题。
1. 三角形按角分类,可以分为( )、
( )、( );按边分类,可以分为( )、( )、
( )。
2. ( )决定圆的位置,( )决定圆的大小。
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
圆心
半径
3. 在同一平面上,过直线外一点,能画已知直线的垂线共( )条,能画已知直线的平行线共( )条。
4. 过一点能画( )条直线,过两点能画( )条直线。
5. 等腰三角形的一个角是45°,另外两个角可能是( )°和( )°或( )°和( )°。
1
1
无数
1
45
90
67.5
67.5
6. 只有一组对边平行,其中一个角是90°的四边形
是( )。
7. ( )具有不稳定性,伸缩门就是应用了这个特性。
8. 把一个长6 cm,宽4 cm的长方形剪成最大的正方形,这个正方形的周长是( )cm,面积是( )cm2。
直角梯形
平行四边形
16
16
9. 一个三角形的面积是12 cm2,和它等底等高的平行四边形的面积是( )cm2。
10. 一个直角三角形的三条边分别是3 cm,4 cm,5 cm,这个三角形的面积是( )cm2,斜边上的高是( )cm。
24
6
2.4
二 选择题。(将正确答案的字母编号填在括号里)
1. ( )具有稳定性,( )具有不稳定性。
A. 三角形 B. 四边形
C. 三角形和四边形
A
B
2. 圆的半径和直径都是一条( ),圆的对称轴是一条( )。
A. 直线 B. 射线 C. 线段
3. 下列选项中,不正确的是( )。
A. 把线段的一端无限延伸,就得到一条射线
B. 大于90°的角是钝角
C. 三角形的内角和是180°
C
A
B
4. 把一个平行四边形拉成长方形,周长( ),面积( )。
A. 不变 B. 变大 C. 变小
5.下图中a,b是两条平行线,三个涂色部分图形的面积相比,( )最大。
A. 平行四边形
B. 三角形
C. 梯形
A
B
A
三 判断题。(正确的在括号里画“√”,错误的画“×”)
1. 延长角的两条边,角就变大了。( )
2. 任意三条线段都能围成一个三角形。( )
3. 正方形是特殊的长方形,长方形是特殊的平行四边形。( )
4. 圆有无数条对称轴。( )
5. 等腰梯形只有一组对边平行,且只有两条边相等。( )
×
×
√
√
×
四 操作题。
1. 量出下面各角的度数。
(1)112°
(2)25°
(3)68°
2. 画并测量从Q点到直线AB的距离。
距离是2 cm。
3. 画出下列图形中底边上的高。
五 按要求计算。(单位:cm)
1. 计算图形的面积。
8×8+8×8×=96(cm2)
2. 计算图形的周长。
4×4=16(cm)
3. 计算阴影部分的面积。
8÷2=4(cm)
8×4-3.14×42÷2=32-25.12=6.88(cm2)
六 解决问题。
1. 已知右图中∠1=35°,∠2=30°,列算式求出其他各角的度数。
∠3=90°-∠2=90°-30°=60°
∠4=90°-∠1=90°-35°=55°
∠5=180°-∠1=180°-35°=145°
∠6=180°-∠5=180°-145°=35°
2. 曲米有两根同样长的小棒,长5 dm,如果她想用三根小棒摆成一个三角形,第3根小棒最长是多少分米(取整分米数)?曲婷给了她一根小棒,结果摆成的三角形的一个底角是35°。顶角是多少度?
第3根小棒<5+5=10(dm)
180°-35°×2=110°
答:第3根小棒最长是9 dm。顶角是110°。
3. 刘大伯用36 m长的篱笆靠墙围了一个鸡圈(如图),这个鸡圈的占地面积是多少平方米?
(36-10)×10÷2=130(m2)
答:这个鸡圈的占地面积是130 m2。
同课章节目录
