2022年小升初数学总复习(通用版) 第23课时 数学广角课件(44张PPT)
文档属性
| 名称 | 2022年小升初数学总复习(通用版) 第23课时 数学广角课件(44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 715.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 09:10:41 | ||
图片预览











文档简介
(共44张PPT)
2
0
2
2
2022年小升初数学复习
全国通用版
专题十一 数学广角
第23课时 数学广角
考点知识梳理
热门考点精讲
目录
小考真题演练
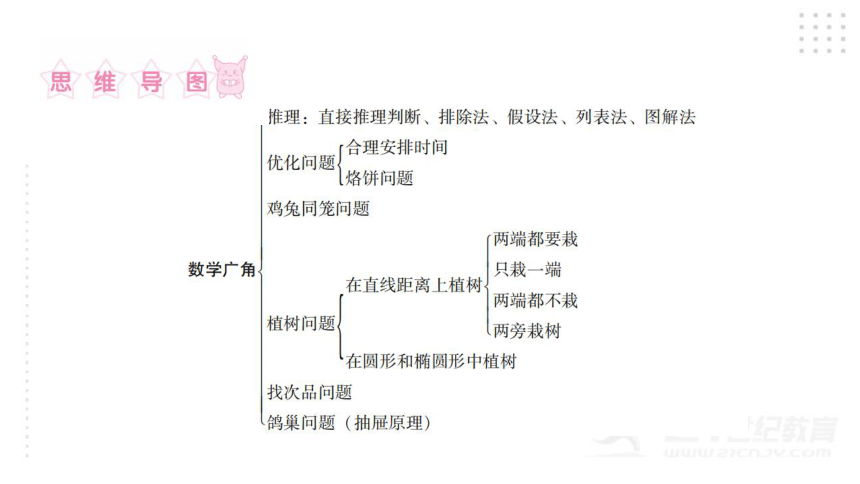
考点知识梳理
1. 推理
常用的推理方法有:直接推理判断、排除法、假设法、列表法、图解法。
2. 优化问题
(1)合理安排时间
①在花时较长的环节中,同步做其他事情。
②让花时更多的人排在后面,别人等待的时间更短。
(2)烙饼问题
烙饼总时间=烙饼总面数÷每次烙饼面数×每次烙饼时间
(除不尽的用 “进一法”保留整数)
例如:每次烙4张饼,两面都要烙,每面3分钟,烙7张饼需要几分钟?
7×2÷4×3=14÷4×3≈4×3=12(分钟)
3. 鸡兔同笼问题
解决方法:列表和假设法
假设法是一种算术方法,可分为“假设——计算——推理——调整(置换)”四个关键步骤。
(1)假设都是鸡:兔的只数=(总足数-总头数×2)÷2
鸡的只数=总头数-兔的只数
(2)假设都是兔:鸡的只数=(总头数×4-总足数)÷2
兔的只数=总头数-鸡的只数
4. 植树问题
(1)在直线距离上植树: 间隔数=总长÷间隔距离。
①两端都要栽:棵数=间隔数+1
②只栽一端:棵数=间隔数
③两端都不栽:棵数=间隔数-1
④两旁栽树:认真审题,不要忘记×2。
(2)在圆形和椭圆形中植树:
棵数=周长÷间距,封闭图形属于“一边栽一边不栽”这种情况,所以棵数=间隔数。
5. 找次品问题
解决方法:把数量尽量平均分成3份,假如不能平均分,3份间尽量只相差1。
6. 鸽巢问题(抽屉原理)
(1)“鸽巢原理”(一):把m个物体任意分放进n个鸽巢中(m和n都是非0自然数,且m>n),那么一定有一个鸽巢中至少放进了2个物体。
(2)“鸽巢原理”(二):把多于kn个物体任意分进n个鸽巢中(k和n都是非0自然数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
(3)应用“鸽巢原理”解题的一般步骤:①分析题意,把实际问题转化成“鸽巢问题”,即弄清楚“鸽巢”(“鸽巢”是什么,有几个鸽巢)和分放的物体;②设计“鸽巢”的具体形式;③运用原理得出某个“鸽巢”中至少分放的物体个数,最终解决问题。
热门考点精讲
考点1:优化问题
亮亮一家每天早上起来都要喝鲜牛奶,亮亮妈妈需要做三件事:取牛奶、热牛奶和洗三个杯子。已知去取牛奶需要1分钟,热牛奶需要5分钟,洗一个杯子需要1分钟,亮亮一家喝到热牛奶最快要用多少分钟
方法指导:本题属于优化问题。首先想取牛奶要1分钟,然后洗杯子的同时可以热牛奶(共用5分钟),最后就能喝到牛奶了。
答案:1+5=6(分)
答:亮亮一家喝到热牛奶最快要用6分钟。
1. 烤面包时,第一面要烤2分钟,烤第二面时只需1分钟。小丽用的烤面包机一次只能放两片面包。她每天早上要吃三片面包,最少要烤多长时间?
给三片面包编上号:1,2,3;先烤1和2的第一面,需要2分钟;然后把1翻面,2拿出换上3,1分钟后1完成拿出;放入2的翻面,1分钟后2完成,3翻面,还需要1分钟;共需要2+1+1+1=5(分钟)。
答:最少需要烤5分钟。
2. 家里来客人了,小明要给客人泡茶。烧水8分钟、洗水壶1分钟、洗茶杯2分钟、接水1分钟、找茶叶1分钟、沏茶1分钟。最快多长时间才能让客人喝上茶?
1+1+8+1=11(分钟),烧水的同时洗茶杯、找茶叶。
答:最快11分钟才能让客人喝上茶。
考点2:鸡兔同笼问题
鸡兔共有100只,鸡与兔的脚共340只,问鸡与兔各多少只?
方法指导:这是一个很典型的鸡兔同笼的问题,已知总的鸡和兔的数量,可以假设都是鸡,则兔的只数=(总足数-总头数×2)÷2,鸡的只数=总头数-兔的只数。
答案:兔的只数=(340-100×2)÷2=70(只)鸡的只数=100-70=30(只)
答:兔有70只,鸡有30只。
3. 六(1)班有38人去旅游,共租了8条船。大船坐6人,小船坐4人,每条船都坐满了。问大小船各租了多少条?(提示:在这里,船就相当于鸡兔的头,船里的人数就相当于鸡兔的脚)
假设8条全是大船,则小船有(8×6-38)÷(6-4)=5(条)
大船有8-5=3(条)
答:大船租了3条,小船租了5条。
4. 买一支铅笔需要1元,买一支钢笔需要5元,小红一共买了10支笔,花了30元。请问铅笔和钢笔各买了几支?
解:设买了铅笔x支,则买了钢笔(10-x)支。
x+5(10-x)=30
x=5
10-5=5(支)
答:买了铅笔5支,买了钢笔5支。
考点3:植树问题
一条河堤136 m,每隔2 m栽一棵垂柳,头尾都栽,一共要栽多少棵垂柳?
方法指导:本题是属于在直线距离上植树的问题,先求间隔数=总长÷间隔距离,两端都要栽,则棵数=间隔数+1。
答案:136÷2+1=68+1=69(棵)
答:一共要栽69棵垂柳。
5. 一个圆形池塘周长为400 m,在岸边每隔4 m栽一棵白杨树,一共能栽多少棵白杨树?
400÷4=100(棵)
答:一共能栽100棵白杨树。
6. 一个正方形的运动场,每边长220 m,每隔10 m安装一盏照明灯,一共可以安装多少盏照明灯?
220×4÷10=88(盏)
答:一共可以安装88盏照明灯。
考点4:找次品问题
一箱糖果有12袋,其中有11袋质量相同,另有1袋质量不足,轻一些。至少称( )次能保证找出这袋糖果来。
方法指导:本题是属于找次品问题,第一次,把12袋糖平均分成3份,任取2份放在天平上,若天平平衡,则较轻的在未取的一份中,若天平不平衡,取较轻的那一份继续;第二次,取含有较轻的一份(4袋),天平两边分别放2袋,找到较轻的一份继续;第三次,取含有较轻的一份(2袋),分别放在天平两侧,即可找到较轻的一袋。
答案:3
7. 从9件物品中找出其中1件次品(略轻一些),把9件物品平均分成( )份称较为合适。
8. 有8瓶水,其中7瓶质量相同,另外有1瓶是糖水,比其他水略重一些,至少称( )次能保证找出这瓶糖水。
9. 有10瓶饮料,其中一瓶变质了(略重一些),用天平称,至少称( ) 次一定能找出次品。
3
2
3
考点5:鸽巢问题(抽屉原理)
某班有男生25人,女生18人,下面说法正确的是( )。A. 至少有2名男生是在同一个月出生的B. 至少有2名女生是在同一个月出生的C. 全班至少有5个人是在同一个月出生的 D. 以上选项都有误
方法指导:本题主要考查用抽屉原理的知识解决实际问题。一年有12个月,因为25÷12=2……1,2+1=3,所以至少有3名男生是在同一个月出生的;18÷12=1……6,1+1=2,至少有2名女生是在同一个月出生的;43÷12=3……7,3+1=4,全班至少有4个人是在同一个月出生的。
答案:B
10. 有3位同学一起练习投篮,如果他们一共投进16个球,那么一定有1位同学至少投进了( )个球。
6
候选人 小华 小红 小明
得票数 正正
11. 某班48名同学投票选一名班长(每人只许投一票),候选人是小华、小红和小明三人,计票一段时间后的统计结果如下表,规定得票最多的人当选,那么后面的计票中小华至少还要得( )票才能当选。
C
A.6 B.7 C.8 D.9
一 填空题。
1. 小文放学排队,从前往后数他是第5个,从后往前数是他是第7个,这一排一共有( )个同学。
2. 抽屉里有4支红铅笔和3支蓝铅笔,如果闭着眼睛摸,一次必须拿( )支,才能保证至少有1支蓝铅笔。
3. 六(1)班有科技书的共28人,有故事书的共26人,两种都有的共10人,两种都没有的共2人,这个班共有学生( )人。
11
5
46
4. 一只平底锅每次只能烙两张饼,用它烙一张饼需要4分钟(正反面各2分钟),那么用它烙3张饼至少需要( )分钟。
5. 小明每天起床要完成的事情有:换校服3分钟,整理床铺2分钟,刷牙、洗脸5分钟,热馒头10分钟,吃早餐5分钟。你认为最合理的安排至少要( )分钟。
6
15
6. 小力、小红、小飞分别获得前三名。 小力说:“我没得到第一名。” 小红说:“我不是第二名。” 小飞说:“小力和小红都比我先到终点。”第一名是( ),第二名是( ),第三名是( )。
小红
小力
小飞
7. 盒里装着5个红球、2个黑球,一次取出一个球,最多摸( )次能保证拿到红色球。
8. 有6瓶水,其中有1瓶是糖水,比其他的水略重一些,可以用天平称量的方法把它找出来,先在天平两边各放( )瓶,至少要称( )次才可以保证把那瓶糖水找出来。
3
2
2
9. 将一根木棒锯成4段需要6分钟,如果每锯一次所需时间都相同,则把这根木棒锯成6段需要( )分钟。
10. 楠楠参加一次知识竞赛,试题共有10道,每做对一题得10分,错一题扣5分,楠楠共得了70分,她做对了( )道题。
10
8
二 选择题。(将正确答案的字母编号填在括号里)
1. 一个盒子里装有黄、白乒乓球各5个,要想使取出的乒乓球中一定有2个黄乒乓球,则至少应取出( )个。
A. 5 B. 6 C. 7
C
2. 10瓶饮料,其中一瓶变质了(略轻一些),用天平称,至少称( )次一定能找出次品。
A. 3 B. 4 C. 5
3. 一根木料锯成3段要6分钟,如果每锯一段所用的时间相同,那么锯成7段需要( )分钟。
A. 14 B. 18 C. 21
A
B
4. 一个圆形跑道200 m,如果每隔10 m立一道警示牌,共需( )道警示牌。
A. 19 B. 20 C. 21
5. 有5个好朋友聚会,每两个人握一次手,一共要握( )次手。
A. 10 B. 16 C. 20
B
A
三 判断题。(正确的在括号里画“√”,错误的画“×”)
1. 从3件物品中找1件次品,至少要用天平称2次才能找出来。( )
2. 圆形水池周围每隔2 m栽一棵树,共栽了40棵,水池的周长是80 m。( )
3. 围棋盘的最外层每边能放19个棋子,最外层一共可以摆放76个棋子。( )
×
√
×
4. 32只鸽子飞回7个鸽舍,总有1个鸽舍至少飞进5只鸽子。( )
5. 鸡和狗共8个头,22只脚,则鸡和狗的只数一样多。( )
√
×
四 解决问题。
1. 一条道路长100 m,在道路的一边每隔5 m种一棵树(两端都要种),一共需要种多少棵树
100÷5+1=21(棵)
答:一共需要种21棵树。
2. 鸡兔同笼,从上面数有48个头,从下面数有126只脚,笼子里的鸡和兔各有多少只?
假设全是兔,则鸡的只数=(4×48-126)÷(4-2)=33(只)
兔的只数:48-33=15(只)
答:笼子里的鸡有33只,兔有15只。
3. 六(2)班有学生55人,每人至少参加赛跑和跳绳比赛中的一种。已知参加赛跑的有36人,参加跳绳的人有38人。问这两项比赛都参加的有几人?
38+36-55=19(人)
答:这两项比赛都参加的有19人。
4. 有15袋花生,其中有一袋比其他的都要轻。
(1)至少用天平称几次能找出轻的那袋?
(1)根据题意,把15袋花生平均分成三份,每份5袋,
第一次,取两份分别放在天平两侧,若天平平衡,则较轻的一袋在未取的一份;若天平不平衡,则取较轻的一份继续称量。
第二次,把含有较轻一袋的5袋分成3份:2袋、2袋、1袋,取2袋的两份分别放在天平两侧,若天平平衡,则较轻的一袋为未取的一袋,若天平不平衡,则取较轻的一份继续称量。
第三次,取含有较轻一袋的2袋,分别放在天平两侧,即可找到较轻的一袋。
答:至少用天平称3次能找出轻的那袋。
(2)用天平称一次有可能找出轻的那一袋吗?为什么?
(2)把15袋花生分成3份:7袋、7袋、1袋,取7袋的两份分别放在天平两侧,若天平平衡,则较轻的一袋为未取的一袋。
答:有可能一次就找到较轻的一袋。
2
0
2
2
2022年小升初数学复习
全国通用版
专题十一 数学广角
第23课时 数学广角
考点知识梳理
热门考点精讲
目录
小考真题演练
考点知识梳理
1. 推理
常用的推理方法有:直接推理判断、排除法、假设法、列表法、图解法。
2. 优化问题
(1)合理安排时间
①在花时较长的环节中,同步做其他事情。
②让花时更多的人排在后面,别人等待的时间更短。
(2)烙饼问题
烙饼总时间=烙饼总面数÷每次烙饼面数×每次烙饼时间
(除不尽的用 “进一法”保留整数)
例如:每次烙4张饼,两面都要烙,每面3分钟,烙7张饼需要几分钟?
7×2÷4×3=14÷4×3≈4×3=12(分钟)
3. 鸡兔同笼问题
解决方法:列表和假设法
假设法是一种算术方法,可分为“假设——计算——推理——调整(置换)”四个关键步骤。
(1)假设都是鸡:兔的只数=(总足数-总头数×2)÷2
鸡的只数=总头数-兔的只数
(2)假设都是兔:鸡的只数=(总头数×4-总足数)÷2
兔的只数=总头数-鸡的只数
4. 植树问题
(1)在直线距离上植树: 间隔数=总长÷间隔距离。
①两端都要栽:棵数=间隔数+1
②只栽一端:棵数=间隔数
③两端都不栽:棵数=间隔数-1
④两旁栽树:认真审题,不要忘记×2。
(2)在圆形和椭圆形中植树:
棵数=周长÷间距,封闭图形属于“一边栽一边不栽”这种情况,所以棵数=间隔数。
5. 找次品问题
解决方法:把数量尽量平均分成3份,假如不能平均分,3份间尽量只相差1。
6. 鸽巢问题(抽屉原理)
(1)“鸽巢原理”(一):把m个物体任意分放进n个鸽巢中(m和n都是非0自然数,且m>n),那么一定有一个鸽巢中至少放进了2个物体。
(2)“鸽巢原理”(二):把多于kn个物体任意分进n个鸽巢中(k和n都是非0自然数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
(3)应用“鸽巢原理”解题的一般步骤:①分析题意,把实际问题转化成“鸽巢问题”,即弄清楚“鸽巢”(“鸽巢”是什么,有几个鸽巢)和分放的物体;②设计“鸽巢”的具体形式;③运用原理得出某个“鸽巢”中至少分放的物体个数,最终解决问题。
热门考点精讲
考点1:优化问题
亮亮一家每天早上起来都要喝鲜牛奶,亮亮妈妈需要做三件事:取牛奶、热牛奶和洗三个杯子。已知去取牛奶需要1分钟,热牛奶需要5分钟,洗一个杯子需要1分钟,亮亮一家喝到热牛奶最快要用多少分钟
方法指导:本题属于优化问题。首先想取牛奶要1分钟,然后洗杯子的同时可以热牛奶(共用5分钟),最后就能喝到牛奶了。
答案:1+5=6(分)
答:亮亮一家喝到热牛奶最快要用6分钟。
1. 烤面包时,第一面要烤2分钟,烤第二面时只需1分钟。小丽用的烤面包机一次只能放两片面包。她每天早上要吃三片面包,最少要烤多长时间?
给三片面包编上号:1,2,3;先烤1和2的第一面,需要2分钟;然后把1翻面,2拿出换上3,1分钟后1完成拿出;放入2的翻面,1分钟后2完成,3翻面,还需要1分钟;共需要2+1+1+1=5(分钟)。
答:最少需要烤5分钟。
2. 家里来客人了,小明要给客人泡茶。烧水8分钟、洗水壶1分钟、洗茶杯2分钟、接水1分钟、找茶叶1分钟、沏茶1分钟。最快多长时间才能让客人喝上茶?
1+1+8+1=11(分钟),烧水的同时洗茶杯、找茶叶。
答:最快11分钟才能让客人喝上茶。
考点2:鸡兔同笼问题
鸡兔共有100只,鸡与兔的脚共340只,问鸡与兔各多少只?
方法指导:这是一个很典型的鸡兔同笼的问题,已知总的鸡和兔的数量,可以假设都是鸡,则兔的只数=(总足数-总头数×2)÷2,鸡的只数=总头数-兔的只数。
答案:兔的只数=(340-100×2)÷2=70(只)鸡的只数=100-70=30(只)
答:兔有70只,鸡有30只。
3. 六(1)班有38人去旅游,共租了8条船。大船坐6人,小船坐4人,每条船都坐满了。问大小船各租了多少条?(提示:在这里,船就相当于鸡兔的头,船里的人数就相当于鸡兔的脚)
假设8条全是大船,则小船有(8×6-38)÷(6-4)=5(条)
大船有8-5=3(条)
答:大船租了3条,小船租了5条。
4. 买一支铅笔需要1元,买一支钢笔需要5元,小红一共买了10支笔,花了30元。请问铅笔和钢笔各买了几支?
解:设买了铅笔x支,则买了钢笔(10-x)支。
x+5(10-x)=30
x=5
10-5=5(支)
答:买了铅笔5支,买了钢笔5支。
考点3:植树问题
一条河堤136 m,每隔2 m栽一棵垂柳,头尾都栽,一共要栽多少棵垂柳?
方法指导:本题是属于在直线距离上植树的问题,先求间隔数=总长÷间隔距离,两端都要栽,则棵数=间隔数+1。
答案:136÷2+1=68+1=69(棵)
答:一共要栽69棵垂柳。
5. 一个圆形池塘周长为400 m,在岸边每隔4 m栽一棵白杨树,一共能栽多少棵白杨树?
400÷4=100(棵)
答:一共能栽100棵白杨树。
6. 一个正方形的运动场,每边长220 m,每隔10 m安装一盏照明灯,一共可以安装多少盏照明灯?
220×4÷10=88(盏)
答:一共可以安装88盏照明灯。
考点4:找次品问题
一箱糖果有12袋,其中有11袋质量相同,另有1袋质量不足,轻一些。至少称( )次能保证找出这袋糖果来。
方法指导:本题是属于找次品问题,第一次,把12袋糖平均分成3份,任取2份放在天平上,若天平平衡,则较轻的在未取的一份中,若天平不平衡,取较轻的那一份继续;第二次,取含有较轻的一份(4袋),天平两边分别放2袋,找到较轻的一份继续;第三次,取含有较轻的一份(2袋),分别放在天平两侧,即可找到较轻的一袋。
答案:3
7. 从9件物品中找出其中1件次品(略轻一些),把9件物品平均分成( )份称较为合适。
8. 有8瓶水,其中7瓶质量相同,另外有1瓶是糖水,比其他水略重一些,至少称( )次能保证找出这瓶糖水。
9. 有10瓶饮料,其中一瓶变质了(略重一些),用天平称,至少称( ) 次一定能找出次品。
3
2
3
考点5:鸽巢问题(抽屉原理)
某班有男生25人,女生18人,下面说法正确的是( )。A. 至少有2名男生是在同一个月出生的B. 至少有2名女生是在同一个月出生的C. 全班至少有5个人是在同一个月出生的 D. 以上选项都有误
方法指导:本题主要考查用抽屉原理的知识解决实际问题。一年有12个月,因为25÷12=2……1,2+1=3,所以至少有3名男生是在同一个月出生的;18÷12=1……6,1+1=2,至少有2名女生是在同一个月出生的;43÷12=3……7,3+1=4,全班至少有4个人是在同一个月出生的。
答案:B
10. 有3位同学一起练习投篮,如果他们一共投进16个球,那么一定有1位同学至少投进了( )个球。
6
候选人 小华 小红 小明
得票数 正正
11. 某班48名同学投票选一名班长(每人只许投一票),候选人是小华、小红和小明三人,计票一段时间后的统计结果如下表,规定得票最多的人当选,那么后面的计票中小华至少还要得( )票才能当选。
C
A.6 B.7 C.8 D.9
一 填空题。
1. 小文放学排队,从前往后数他是第5个,从后往前数是他是第7个,这一排一共有( )个同学。
2. 抽屉里有4支红铅笔和3支蓝铅笔,如果闭着眼睛摸,一次必须拿( )支,才能保证至少有1支蓝铅笔。
3. 六(1)班有科技书的共28人,有故事书的共26人,两种都有的共10人,两种都没有的共2人,这个班共有学生( )人。
11
5
46
4. 一只平底锅每次只能烙两张饼,用它烙一张饼需要4分钟(正反面各2分钟),那么用它烙3张饼至少需要( )分钟。
5. 小明每天起床要完成的事情有:换校服3分钟,整理床铺2分钟,刷牙、洗脸5分钟,热馒头10分钟,吃早餐5分钟。你认为最合理的安排至少要( )分钟。
6
15
6. 小力、小红、小飞分别获得前三名。 小力说:“我没得到第一名。” 小红说:“我不是第二名。” 小飞说:“小力和小红都比我先到终点。”第一名是( ),第二名是( ),第三名是( )。
小红
小力
小飞
7. 盒里装着5个红球、2个黑球,一次取出一个球,最多摸( )次能保证拿到红色球。
8. 有6瓶水,其中有1瓶是糖水,比其他的水略重一些,可以用天平称量的方法把它找出来,先在天平两边各放( )瓶,至少要称( )次才可以保证把那瓶糖水找出来。
3
2
2
9. 将一根木棒锯成4段需要6分钟,如果每锯一次所需时间都相同,则把这根木棒锯成6段需要( )分钟。
10. 楠楠参加一次知识竞赛,试题共有10道,每做对一题得10分,错一题扣5分,楠楠共得了70分,她做对了( )道题。
10
8
二 选择题。(将正确答案的字母编号填在括号里)
1. 一个盒子里装有黄、白乒乓球各5个,要想使取出的乒乓球中一定有2个黄乒乓球,则至少应取出( )个。
A. 5 B. 6 C. 7
C
2. 10瓶饮料,其中一瓶变质了(略轻一些),用天平称,至少称( )次一定能找出次品。
A. 3 B. 4 C. 5
3. 一根木料锯成3段要6分钟,如果每锯一段所用的时间相同,那么锯成7段需要( )分钟。
A. 14 B. 18 C. 21
A
B
4. 一个圆形跑道200 m,如果每隔10 m立一道警示牌,共需( )道警示牌。
A. 19 B. 20 C. 21
5. 有5个好朋友聚会,每两个人握一次手,一共要握( )次手。
A. 10 B. 16 C. 20
B
A
三 判断题。(正确的在括号里画“√”,错误的画“×”)
1. 从3件物品中找1件次品,至少要用天平称2次才能找出来。( )
2. 圆形水池周围每隔2 m栽一棵树,共栽了40棵,水池的周长是80 m。( )
3. 围棋盘的最外层每边能放19个棋子,最外层一共可以摆放76个棋子。( )
×
√
×
4. 32只鸽子飞回7个鸽舍,总有1个鸽舍至少飞进5只鸽子。( )
5. 鸡和狗共8个头,22只脚,则鸡和狗的只数一样多。( )
√
×
四 解决问题。
1. 一条道路长100 m,在道路的一边每隔5 m种一棵树(两端都要种),一共需要种多少棵树
100÷5+1=21(棵)
答:一共需要种21棵树。
2. 鸡兔同笼,从上面数有48个头,从下面数有126只脚,笼子里的鸡和兔各有多少只?
假设全是兔,则鸡的只数=(4×48-126)÷(4-2)=33(只)
兔的只数:48-33=15(只)
答:笼子里的鸡有33只,兔有15只。
3. 六(2)班有学生55人,每人至少参加赛跑和跳绳比赛中的一种。已知参加赛跑的有36人,参加跳绳的人有38人。问这两项比赛都参加的有几人?
38+36-55=19(人)
答:这两项比赛都参加的有19人。
4. 有15袋花生,其中有一袋比其他的都要轻。
(1)至少用天平称几次能找出轻的那袋?
(1)根据题意,把15袋花生平均分成三份,每份5袋,
第一次,取两份分别放在天平两侧,若天平平衡,则较轻的一袋在未取的一份;若天平不平衡,则取较轻的一份继续称量。
第二次,把含有较轻一袋的5袋分成3份:2袋、2袋、1袋,取2袋的两份分别放在天平两侧,若天平平衡,则较轻的一袋为未取的一袋,若天平不平衡,则取较轻的一份继续称量。
第三次,取含有较轻一袋的2袋,分别放在天平两侧,即可找到较轻的一袋。
答:至少用天平称3次能找出轻的那袋。
(2)用天平称一次有可能找出轻的那一袋吗?为什么?
(2)把15袋花生分成3份:7袋、7袋、1袋,取7袋的两份分别放在天平两侧,若天平平衡,则较轻的一袋为未取的一袋。
答:有可能一次就找到较轻的一袋。
同课章节目录
