人教版五年级数学下册 2.1 因数和倍数课件(共14张PPT)
文档属性
| 名称 | 人教版五年级数学下册 2.1 因数和倍数课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 13:48:12 | ||
图片预览



文档简介
(共14张PPT)
因数与倍数
1. 因数和倍数
因数与倍数
一、复习导入
34÷2=
2÷4=
18÷6=
口算下面各题,说说谁是谁的倍数?谁是谁的因数?
34÷2=17,商是整数而没有余数,所以34是2和17的倍数,2和17是34的因数。
17
2÷4=0.5,商是小数不是整数,没有因数和倍数的关系。
18÷6=3,商是整数而没有余数,所以18是6和3的倍数,6和3是18的因数。
0.5
3
二、探究新知
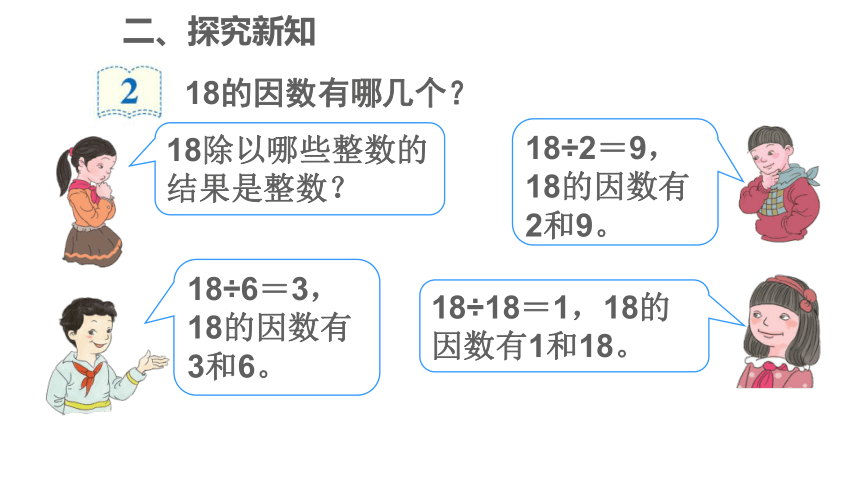
18的因数有哪几个?
18除以哪些整数的结果是整数?
18÷2=9,18的因数有2和9。
18÷6=3,18的因数有3和6。
18÷18=1,18的因数有1和18。
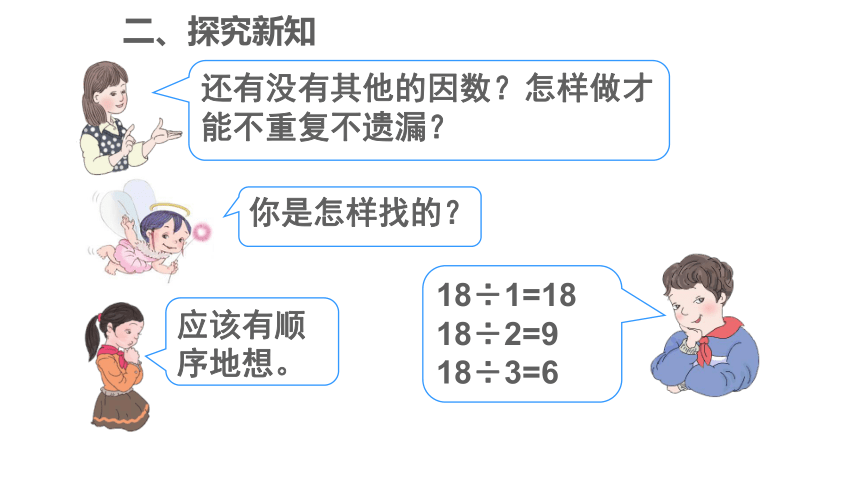
还有没有其他的因数?怎样做才能不重复不遗漏?
你是怎样找的?
18÷1=18
18÷2=9
18÷3=6
应该有顺序地想。
二、探究新知
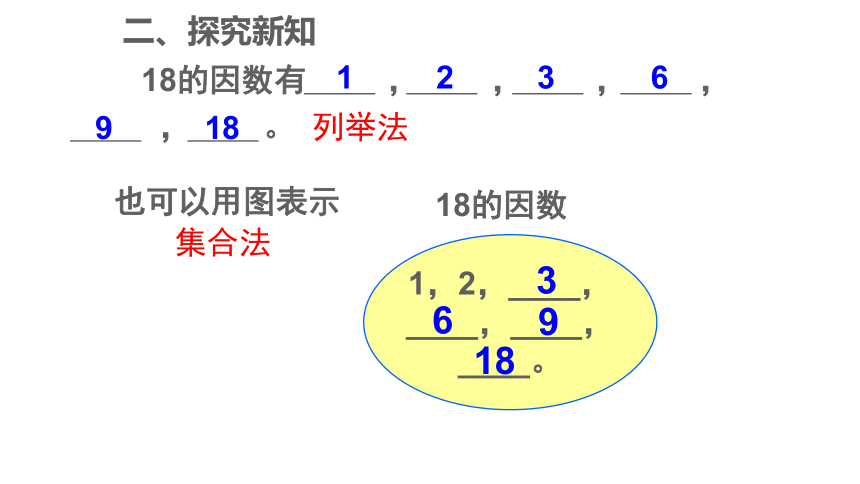
18的因数有 , , , ,
, 。
1
2
3
6
9
18
也可以用图表示
1,2,____,
____,____,
____。
18的因数
3
6
9
18
二、探究新知
列举法
集合法
30的因数有哪些?36呢?
30的因数有:1,2,3,
5,6,10,15,30。
36的因数有:1,2,3,
4,6,9,12,18,36。
30÷1=30
30÷2=15
30÷3=10
30÷5=6
36÷1=36
36÷2=18
36÷3=12
36÷4=9
36÷6=6
二、探究新知
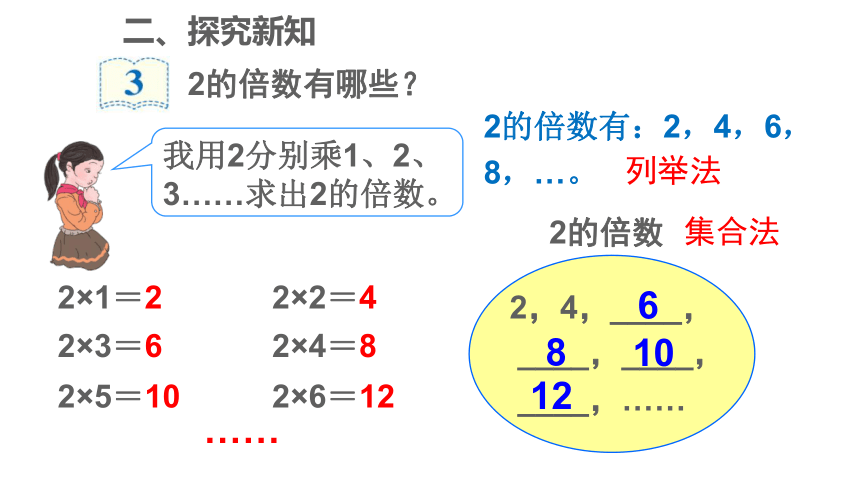
2的倍数有哪些?
我用2分别乘1、2、3……求出2的倍数。
2×1=2
2×2=4
2×3=6
2×4=8
2×5=10
2×6=12
……
2,4,____,
____,____,
____,……
2的倍数
6
8
10
12
二、探究新知
2的倍数有:2,4,6,
8,…。
列举法
集合法
3的倍数有哪些?5呢?
3的倍数有:3,6 ,9,12,15,…。
5的倍数有:5,10,15,20,25,…。
3×1=3
3×2=6
3×3=9
3×4=12
3×5=15
……
5×1=5
5×2=10
5×3=15
5×4=20
5×5=25
……
二、探究新知
从上面找因数和倍数的过程中,你有什么发现?
一个数的最小因数是( ),最大因数是( )。
一个数的最小倍数是( )。有最大倍数吗?
1
它本身
它本身
一个数的因数的个数是有限的,而倍数的个数是无限的。
二、探究新知
三、巩固练习
1.把中间符合条件的数填入相应的热气球里。
(教材练习二第1题)
1
2
3
4
6
9
12
36
18
1
2
3
4
5
6
10
12
15
20
30
60
2.把是5的倍数的星星涂上黄色。(教材练习二第3题)
5
60
10
55
100
35
三、巩固练习
(3)36÷9=4,所以36是9的倍数。 ( )
3.下面的说法正确吗?正确的画“√”,错误的画“×”。(教材练习二第5题)
(1)1是1,2,3,…的因数。 ( )
(2)8的倍数只有16,24,32,40,48。( )
(4)5.7是3的倍数。 ( )
√
×
×
√
三、巩固练习
四、课堂小结
从从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。
1.找一个数的因数的方法:列除法算式找,有此数分
别除以大于等于1且小于等于它本身的所有整数,
所得的商是整数而没有余数,这些除数和商就是这
个的因数。
2.表示一个数的因数的方法:列举法和集合法。
3.一个数的因数的特征:一个数的因数的个数是有限
的,其中最小的因数是1,最大的因数是它本身。
四、课堂小结
从从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。
4.找一个数的倍数的方法:列乘法算式找,用这个数
依次与非0自然数相乘,所得的积就是这个数的倍数。
5.表示一个数的倍数的方法:列举法和集合法。
6.一个数的倍数的特征:一个数的倍数的个数是无限
的,其中最小的倍数是它本身,没有最大的因数。
因数与倍数
1. 因数和倍数
因数与倍数
一、复习导入
34÷2=
2÷4=
18÷6=
口算下面各题,说说谁是谁的倍数?谁是谁的因数?
34÷2=17,商是整数而没有余数,所以34是2和17的倍数,2和17是34的因数。
17
2÷4=0.5,商是小数不是整数,没有因数和倍数的关系。
18÷6=3,商是整数而没有余数,所以18是6和3的倍数,6和3是18的因数。
0.5
3
二、探究新知
18的因数有哪几个?
18除以哪些整数的结果是整数?
18÷2=9,18的因数有2和9。
18÷6=3,18的因数有3和6。
18÷18=1,18的因数有1和18。
还有没有其他的因数?怎样做才能不重复不遗漏?
你是怎样找的?
18÷1=18
18÷2=9
18÷3=6
应该有顺序地想。
二、探究新知
18的因数有 , , , ,
, 。
1
2
3
6
9
18
也可以用图表示
1,2,____,
____,____,
____。
18的因数
3
6
9
18
二、探究新知
列举法
集合法
30的因数有哪些?36呢?
30的因数有:1,2,3,
5,6,10,15,30。
36的因数有:1,2,3,
4,6,9,12,18,36。
30÷1=30
30÷2=15
30÷3=10
30÷5=6
36÷1=36
36÷2=18
36÷3=12
36÷4=9
36÷6=6
二、探究新知
2的倍数有哪些?
我用2分别乘1、2、3……求出2的倍数。
2×1=2
2×2=4
2×3=6
2×4=8
2×5=10
2×6=12
……
2,4,____,
____,____,
____,……
2的倍数
6
8
10
12
二、探究新知
2的倍数有:2,4,6,
8,…。
列举法
集合法
3的倍数有哪些?5呢?
3的倍数有:3,6 ,9,12,15,…。
5的倍数有:5,10,15,20,25,…。
3×1=3
3×2=6
3×3=9
3×4=12
3×5=15
……
5×1=5
5×2=10
5×3=15
5×4=20
5×5=25
……
二、探究新知
从上面找因数和倍数的过程中,你有什么发现?
一个数的最小因数是( ),最大因数是( )。
一个数的最小倍数是( )。有最大倍数吗?
1
它本身
它本身
一个数的因数的个数是有限的,而倍数的个数是无限的。
二、探究新知
三、巩固练习
1.把中间符合条件的数填入相应的热气球里。
(教材练习二第1题)
1
2
3
4
6
9
12
36
18
1
2
3
4
5
6
10
12
15
20
30
60
2.把是5的倍数的星星涂上黄色。(教材练习二第3题)
5
60
10
55
100
35
三、巩固练习
(3)36÷9=4,所以36是9的倍数。 ( )
3.下面的说法正确吗?正确的画“√”,错误的画“×”。(教材练习二第5题)
(1)1是1,2,3,…的因数。 ( )
(2)8的倍数只有16,24,32,40,48。( )
(4)5.7是3的倍数。 ( )
√
×
×
√
三、巩固练习
四、课堂小结
从从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。
1.找一个数的因数的方法:列除法算式找,有此数分
别除以大于等于1且小于等于它本身的所有整数,
所得的商是整数而没有余数,这些除数和商就是这
个的因数。
2.表示一个数的因数的方法:列举法和集合法。
3.一个数的因数的特征:一个数的因数的个数是有限
的,其中最小的因数是1,最大的因数是它本身。
四、课堂小结
从从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。从同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。同一个方向观察物体,只要对着原来物体的前面或后面的任意1 个正方体添 1 个正方体,所看到的形状都不变。
4.找一个数的倍数的方法:列乘法算式找,用这个数
依次与非0自然数相乘,所得的积就是这个数的倍数。
5.表示一个数的倍数的方法:列举法和集合法。
6.一个数的倍数的特征:一个数的倍数的个数是无限
的,其中最小的倍数是它本身,没有最大的因数。
