2022届高三冲刺高考(文科数学)基本初等函数、函数与方程课件(共24张PPT)
文档属性
| 名称 | 2022届高三冲刺高考(文科数学)基本初等函数、函数与方程课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-02 18:30:58 | ||
图片预览




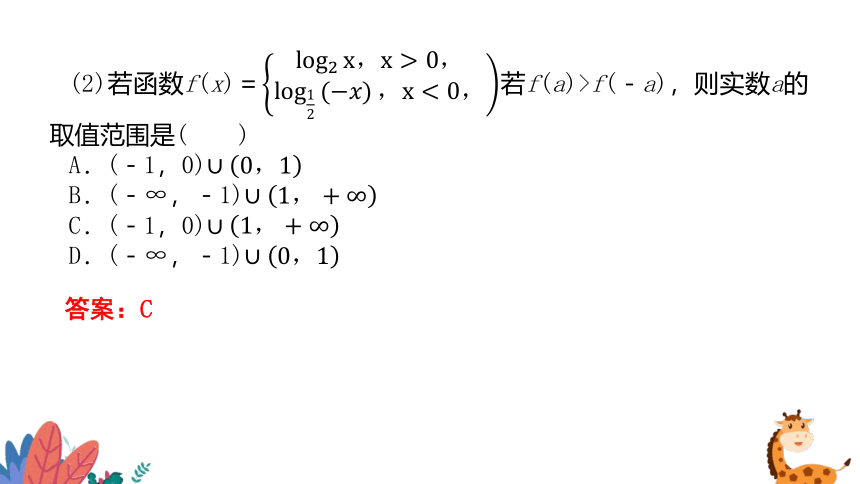


文档简介
(共24张PPT)
冲刺高考 (文科数学)
基本初等函数、函数与方程
考点一 基本初等函数的图象与性质——对比学习,类比应用
1.指数与对数式的七个运算公式
(1)am·an=________;
(2)(am)n=________;
(3)loga(MN)=____________;
(4)loga=_____________;
(5)logaMn=________;
(6)alogaN=________;
(7)logaN=________.
注:a>0且a≠1,b>0且b≠1,M>0,N>0.
am+n
amn
logaM+logaN
logaM-logaN
nlogaM
N
2.指数函数与对数函数的图象和性质
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象和性质,分01两种情况,当a>1时,两函数在定义域内都为________,当0增函数
减函数
[例1] (1)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为(≈1.259)( )
A.1.5 B.1.2
C.0.8 D.0.6
解析:4.9=5+lg V lg V=-0.1 V==≈≈0.8,所以该同学视力的小数记录法的数据约为0.8.
答案:C
(2)若函数f(x)=若f(a)>f(-a),则实数a的取值范围是( )
A.(-1,0)
B.(-∞,-1)
C.(-1,0)
D.(-∞,-1)
答案:C
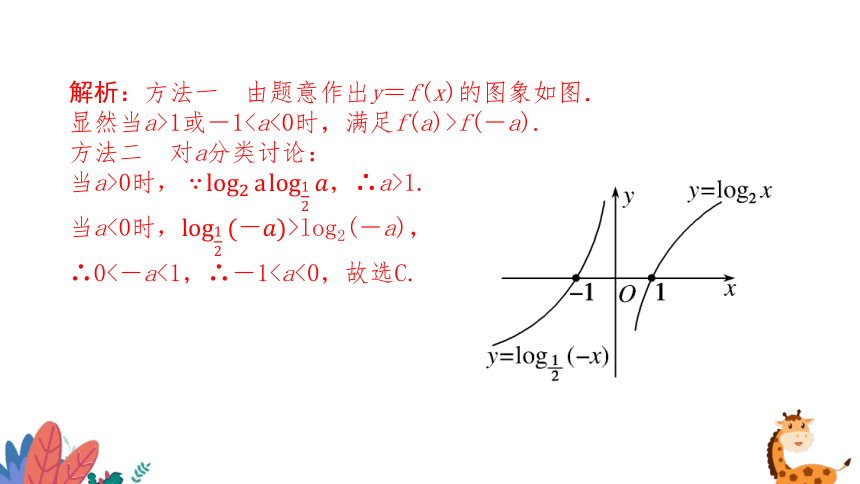
解析:方法一 由题意作出y=f(x)的图象如图.
显然当a>1或-1f(-a).
方法二 对a分类讨论:
当a>0时,∴a>1.
当a<0时>log2(-a),
∴0<-a<1,∴-1(3)已知a=0.3-0.2,b=log0.20.3,c=log0.32,则( )
A.a>b>c B.a>c>b
C.b>c>a D.c>b>a
答案:A
解析:由指数函数的性质,得a=0.3-0.2>0.30=1.
由对数函数的性质,得b=log0.20.3log0.21=0,
可知0于是有a>b>c.故选A.
对点训练
1.设a=30.7,b=,c=log0.70.8,则a,b,c的大小关系为( )
A.aC.b解析:由题知c=log0.70.8<1,b==30.8,易知函数y=3x在R上单调递增,所以b=30.8>30.7=a>1,所以c答案:D
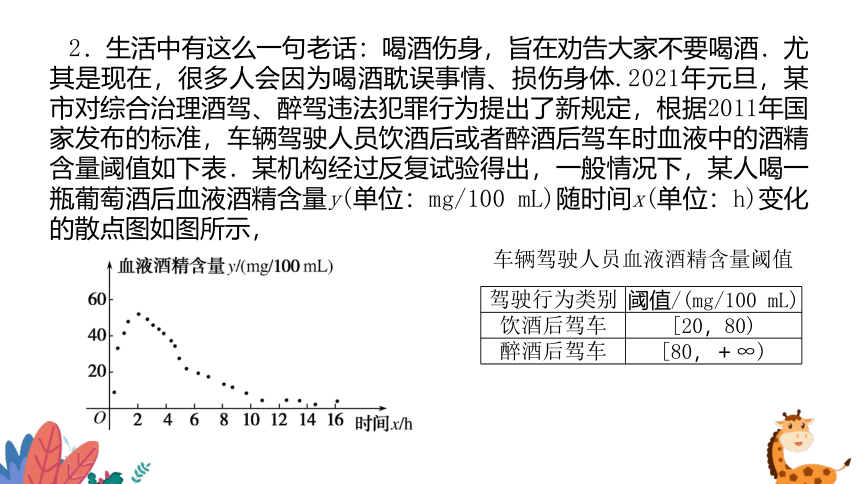
2.生活中有这么一句老话:喝酒伤身,旨在劝告大家不要喝酒.尤其是现在,很多人会因为喝酒耽误事情、损伤身体.2021年元旦,某市对综合治理酒驾、醉驾违法犯罪行为提出了新规定,根据2011年国家发布的标准,车辆驾驶人员饮酒后或者醉酒后驾车时血液中的酒精含量阈值如下表.某机构经过反复试验得出,一般情况下,某人喝一瓶葡萄酒后血液酒精含量y(单位:mg/100 mL)随时间x(单位:h)变化的散点图如图所示,
车辆驾驶人员血液酒精含量阈值
驾驶行为类别 阈值/(mg/100 mL)
饮酒后驾车 [20,80)
醉酒后驾车 [80,+∞)
且该图表示的函数模型为y=假设该人喝一瓶葡萄酒后至少经过n(n∈N*)小时才可以驾车,则n的值为(参考数据:ln 15≈2.71)( )
A.4 B.5
C.6 D.7
答案:C
解析:由散点图可知,该人喝一瓶葡萄酒后的2个小时内,其血液酒精含量持续增大至大于20 mg/100 mL,故2小时内不能驾车.
令90·e-0.5n+14<20,即e-0.5n<,
解得n>2ln 15≈2×2.71=5.42,
所以n的最小值为6,故该人至少经过6小时才可以驾车.
故选C.
3.已知函数f(x)=若f(e)=-3f(0),则b=________,函数f(x)的值域为___________________.
解析:由f(e)=-3f(0)得1+b=-3×(-1),即b=2,
即函数f(x)=当x>1时,y=ln x+2>2;当x≤1时,y=ex-2∈(-2,e-2].故函数f(x)的值域为(-2,e-2]
2
(-2,e-2]
考点二 函数的零点——“零点”“实根”相互转化
1.函数的零点及其方程根的关系
对于函数f(x),使f(x)=0的实数x叫做函数f(x)的零点.函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的________.
2.零点存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
横坐标
角度1 确定函数零点的个数或其存在范围
[例2] (1)函数f(x)=log3x+x-2的零点所在的区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
答案:B
解析:(1)方法一(定理法) 函数f(x)=log3x+x-2的定义域为(0,+∞),并且f(x)在(0,+∞)上单调递增,图象是一条连续的曲线.
由题意知f(1)=-1<0,f(2)=log32>0,f(3)=2>0,
根据零点存在性定理可知,函数f(x)=log3x+x-2有唯一零点,且零点在区间(1,2)内.故选B.
方法二(图象法) 将函数f(x)的零点所在的区间转化为函数g(x)=log3x,h(x)=-x+2图象交点的横坐标所在的范围,作出两函数图象如图所示,可知f(x)的零点所在的区间为(1,2).故选B.
(2)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log3|x|的零点个数是( )
A.5 B.4
C.3 D.2
答案:B
解析:∵偶函数f(x)满足f(x+2)=f(x),∴函数的周期为2.当x∈[0,1]时,f(x)=x,故当x∈[-1,0]时,f(x)=-x.函数y=f(x)-log3|x|的零点个数等于函数y=f(x)的图象与函数y=log3|x|的图象的交点个数.在同一个坐标系中画出函数y=f(x)的图象与函数y=log3|x|的图象,如图所示.显然函数y=f(x)的图象与函数y=log3|x|的图象有4个交点,故选B.
角度2 根据函数的零点求参数的取值或范围
[例3] [2021·成都市诊断性检测]已知定义在R上的函数f(x)满足f(2-x)=f(2+x),当x≤2时,f(x)=-1.若关于x的方程f(x)-kx+2k-e+1=0有三个不相等的实数根,则实数k的取值范围是( )
A.(-2,0)
C.(-e,0)
答案:D
解析:关于x的方程f(x)-kx+2k-e+1=0有三个不相等的实数根等价于函数f(x)的图象与y=k(x-2)+e-1的图象有三个不同的交点.y=k(x-2)+e-1过定点(2,e-1).当x≤2时,f′(x)=ex+(x-1)ex=xex,所以函数f(x)在(-∞,0)上单调递减,在[0,2]上单调递增,因为f(2-x)=f(2+x),所以函数f(x)的图象关于
直线x=2对称,所以函数f(x)在(2,4]上
单调递减,在(4,+∞)上单调递增.f(0)
=-2,f(2)=e2-1,x<0时,f(x)<0.在同
一平面直角坐标系中,分别作出直线y=
k(x-2)+e-1,函数f(x)的图象,如图所示.
当x≤2时,设直线y=k(x-2)+e-1与f(x)的图象相切时的切点为(m,(m-1)em-1),m≤2.因为f′(m)=mem,所以切线的方程为y-(m-1)em+1=mem(x-m),因为直线过定点(2,e-1),所以e-1-(m-1)em +1=mem(2-m),即e-(m-1)em=mem(2-m),所以m=1,此时直线的斜率为f′(1)=e.由图象可得满足条件的实数k的取值范围为(0,e),
当x>2时,根据图象的对称性可知满足条件的实数k的取值范围为(-e,0).综上,实数k的取值范围为(-e,0)
对点训练
1.已知实数a>1,0A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
解析:∵a>1,00.由零点存在性定理可知,f(x)的零点在区间(-1,0)内.
答案:B
2.已知函数f(x)=若f(x0)=-1,则x0=________;若关于x的方程f(x)=k有两个不同零点,则实数k的取值范围是________.
解析:解方程f(x0)=-1,得或解得x0=-1.关于x的方程f(x)=k有两个不同零点等价于y=f(x)的图象与直线y=k有两个不同交点,观察图象可知:当0-1
(0,1)
[例4] 中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85 ℃的水泡制,等到茶水温度降至60 ℃时饮用,可以产生最佳口感.为分析泡制一杯最佳口感的茶水所需的时间,某研究人员每隔1 min测量一次茶水的温度,根据所得数据作出如图所示的散点图.观察散点图的分布情况,下列可以近似地刻画茶水温度y随时间x变化的规律的函数模型是( )
A.y=mx2+n(m>0)
B.y=mx+n(m>0)
C.y=max+n(m>0,a>0且a≠1)
D.y=mlogax+n(m>0,a>0且a≠1)
答案:C
解析:由散点图的连线是曲线可知,B选项不符合题意;因为A中的函数是二次函数,其图象对称轴为y轴,与题中图象不符,故排除A;D中的函数图象过定点(1,n),且必穿过x轴,D选项不符题意.故符合条件的只有指数函数图象,故选C.
Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)( )
A.60 B.63 C.66 D.69
解析:I(t*)==0.95K,整理可得e0.23(t*-53)=19,两边取自然对数得0.23(t*-53)=ln 19≈3,解得t*≈66,故选C.
答案:C
冲刺高考 (文科数学)
基本初等函数、函数与方程
考点一 基本初等函数的图象与性质——对比学习,类比应用
1.指数与对数式的七个运算公式
(1)am·an=________;
(2)(am)n=________;
(3)loga(MN)=____________;
(4)loga=_____________;
(5)logaMn=________;
(6)alogaN=________;
(7)logaN=________.
注:a>0且a≠1,b>0且b≠1,M>0,N>0.
am+n
amn
logaM+logaN
logaM-logaN
nlogaM
N
2.指数函数与对数函数的图象和性质
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象和性质,分0
减函数
[例1] (1)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为(≈1.259)( )
A.1.5 B.1.2
C.0.8 D.0.6
解析:4.9=5+lg V lg V=-0.1 V==≈≈0.8,所以该同学视力的小数记录法的数据约为0.8.
答案:C
(2)若函数f(x)=若f(a)>f(-a),则实数a的取值范围是( )
A.(-1,0)
B.(-∞,-1)
C.(-1,0)
D.(-∞,-1)
答案:C
解析:方法一 由题意作出y=f(x)的图象如图.
显然当a>1或-1
方法二 对a分类讨论:
当a>0时,∴a>1.
当a<0时>log2(-a),
∴0<-a<1,∴-1
A.a>b>c B.a>c>b
C.b>c>a D.c>b>a
答案:A
解析:由指数函数的性质,得a=0.3-0.2>0.30=1.
由对数函数的性质,得b=log0.20.3
可知0
对点训练
1.设a=30.7,b=,c=log0.70.8,则a,b,c的大小关系为( )
A.a
2.生活中有这么一句老话:喝酒伤身,旨在劝告大家不要喝酒.尤其是现在,很多人会因为喝酒耽误事情、损伤身体.2021年元旦,某市对综合治理酒驾、醉驾违法犯罪行为提出了新规定,根据2011年国家发布的标准,车辆驾驶人员饮酒后或者醉酒后驾车时血液中的酒精含量阈值如下表.某机构经过反复试验得出,一般情况下,某人喝一瓶葡萄酒后血液酒精含量y(单位:mg/100 mL)随时间x(单位:h)变化的散点图如图所示,
车辆驾驶人员血液酒精含量阈值
驾驶行为类别 阈值/(mg/100 mL)
饮酒后驾车 [20,80)
醉酒后驾车 [80,+∞)
且该图表示的函数模型为y=假设该人喝一瓶葡萄酒后至少经过n(n∈N*)小时才可以驾车,则n的值为(参考数据:ln 15≈2.71)( )
A.4 B.5
C.6 D.7
答案:C
解析:由散点图可知,该人喝一瓶葡萄酒后的2个小时内,其血液酒精含量持续增大至大于20 mg/100 mL,故2小时内不能驾车.
令90·e-0.5n+14<20,即e-0.5n<,
解得n>2ln 15≈2×2.71=5.42,
所以n的最小值为6,故该人至少经过6小时才可以驾车.
故选C.
3.已知函数f(x)=若f(e)=-3f(0),则b=________,函数f(x)的值域为___________________.
解析:由f(e)=-3f(0)得1+b=-3×(-1),即b=2,
即函数f(x)=当x>1时,y=ln x+2>2;当x≤1时,y=ex-2∈(-2,e-2].故函数f(x)的值域为(-2,e-2]
2
(-2,e-2]
考点二 函数的零点——“零点”“实根”相互转化
1.函数的零点及其方程根的关系
对于函数f(x),使f(x)=0的实数x叫做函数f(x)的零点.函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)的图象与函数y=g(x)的图象交点的________.
2.零点存在性定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
横坐标
角度1 确定函数零点的个数或其存在范围
[例2] (1)函数f(x)=log3x+x-2的零点所在的区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
答案:B
解析:(1)方法一(定理法) 函数f(x)=log3x+x-2的定义域为(0,+∞),并且f(x)在(0,+∞)上单调递增,图象是一条连续的曲线.
由题意知f(1)=-1<0,f(2)=log32>0,f(3)=2>0,
根据零点存在性定理可知,函数f(x)=log3x+x-2有唯一零点,且零点在区间(1,2)内.故选B.
方法二(图象法) 将函数f(x)的零点所在的区间转化为函数g(x)=log3x,h(x)=-x+2图象交点的横坐标所在的范围,作出两函数图象如图所示,可知f(x)的零点所在的区间为(1,2).故选B.
(2)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log3|x|的零点个数是( )
A.5 B.4
C.3 D.2
答案:B
解析:∵偶函数f(x)满足f(x+2)=f(x),∴函数的周期为2.当x∈[0,1]时,f(x)=x,故当x∈[-1,0]时,f(x)=-x.函数y=f(x)-log3|x|的零点个数等于函数y=f(x)的图象与函数y=log3|x|的图象的交点个数.在同一个坐标系中画出函数y=f(x)的图象与函数y=log3|x|的图象,如图所示.显然函数y=f(x)的图象与函数y=log3|x|的图象有4个交点,故选B.
角度2 根据函数的零点求参数的取值或范围
[例3] [2021·成都市诊断性检测]已知定义在R上的函数f(x)满足f(2-x)=f(2+x),当x≤2时,f(x)=-1.若关于x的方程f(x)-kx+2k-e+1=0有三个不相等的实数根,则实数k的取值范围是( )
A.(-2,0)
C.(-e,0)
答案:D
解析:关于x的方程f(x)-kx+2k-e+1=0有三个不相等的实数根等价于函数f(x)的图象与y=k(x-2)+e-1的图象有三个不同的交点.y=k(x-2)+e-1过定点(2,e-1).当x≤2时,f′(x)=ex+(x-1)ex=xex,所以函数f(x)在(-∞,0)上单调递减,在[0,2]上单调递增,因为f(2-x)=f(2+x),所以函数f(x)的图象关于
直线x=2对称,所以函数f(x)在(2,4]上
单调递减,在(4,+∞)上单调递增.f(0)
=-2,f(2)=e2-1,x<0时,f(x)<0.在同
一平面直角坐标系中,分别作出直线y=
k(x-2)+e-1,函数f(x)的图象,如图所示.
当x≤2时,设直线y=k(x-2)+e-1与f(x)的图象相切时的切点为(m,(m-1)em-1),m≤2.因为f′(m)=mem,所以切线的方程为y-(m-1)em+1=mem(x-m),因为直线过定点(2,e-1),所以e-1-(m-1)em +1=mem(2-m),即e-(m-1)em=mem(2-m),所以m=1,此时直线的斜率为f′(1)=e.由图象可得满足条件的实数k的取值范围为(0,e),
当x>2时,根据图象的对称性可知满足条件的实数k的取值范围为(-e,0).综上,实数k的取值范围为(-e,0)
对点训练
1.已知实数a>1,0
C.(0,1) D.(1,2)
解析:∵a>1,0
答案:B
2.已知函数f(x)=若f(x0)=-1,则x0=________;若关于x的方程f(x)=k有两个不同零点,则实数k的取值范围是________.
解析:解方程f(x0)=-1,得或解得x0=-1.关于x的方程f(x)=k有两个不同零点等价于y=f(x)的图象与直线y=k有两个不同交点,观察图象可知:当0
(0,1)
[例4] 中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85 ℃的水泡制,等到茶水温度降至60 ℃时饮用,可以产生最佳口感.为分析泡制一杯最佳口感的茶水所需的时间,某研究人员每隔1 min测量一次茶水的温度,根据所得数据作出如图所示的散点图.观察散点图的分布情况,下列可以近似地刻画茶水温度y随时间x变化的规律的函数模型是( )
A.y=mx2+n(m>0)
B.y=mx+n(m>0)
C.y=max+n(m>0,a>0且a≠1)
D.y=mlogax+n(m>0,a>0且a≠1)
答案:C
解析:由散点图的连线是曲线可知,B选项不符合题意;因为A中的函数是二次函数,其图象对称轴为y轴,与题中图象不符,故排除A;D中的函数图象过定点(1,n),且必穿过x轴,D选项不符题意.故符合条件的只有指数函数图象,故选C.
Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)( )
A.60 B.63 C.66 D.69
解析:I(t*)==0.95K,整理可得e0.23(t*-53)=19,两边取自然对数得0.23(t*-53)=ln 19≈3,解得t*≈66,故选C.
答案:C
同课章节目录
