人教版 五年级下册数学 2.1因数与倍数 同步作业 (含答案)
文档属性
| 名称 | 人教版 五年级下册数学 2.1因数与倍数 同步作业 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 75.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 15:45:55 | ||
图片预览


文档简介
同步作业 2.1因数与倍数 2021-2022学年下学期小学数学人教新版五年级
一.选择题(共6小题)
1.要使3□5是3的倍数,方框里最大可以填( )
A.7 B.9 C.4
2.200多年前,德国数学家哥德巴赫发现:每一个大于4的偶数,都可以表示成两个奇素数之和。下面第( )个算式符合上面的发现。
A.45=2+43 B.40=11+29 C.38=25+13
3.下面几组数,全部都是质数的是( )
A.19,1,13 B.7,9,51 C.87,17,5 D.2,29,41
4.一个小于50的自然数,既是8的倍数,又是10的倍数,这个数是( )
A.8 B.10 C.40
5.合数的因数有( )
A.1个 B.3个 C.两个以上
6.一个数,既是40的因数又是5的倍数,这样的数有( )个。
A.1 B.2 C.3 D.4
二.填空题(共5小题)
7.12的因数有 其中 是奇数, 是质数, 是合数。
8. 既不是质数也不是合数。10以内的质数有 。
9.在45,6和9中, 是 的因数。
10.在1到20的自然数中,最大的质数是 ,共有 个合数。
11.“哥德巴赫猜想”认为,每个不小于6的偶数都可写成两个奇素数(既是奇数,又是质数)之和。如6=3+3,8=3+5,10=3+7=5+5,……100写成两个奇素数之和是 。
三.操作题(共1小题)
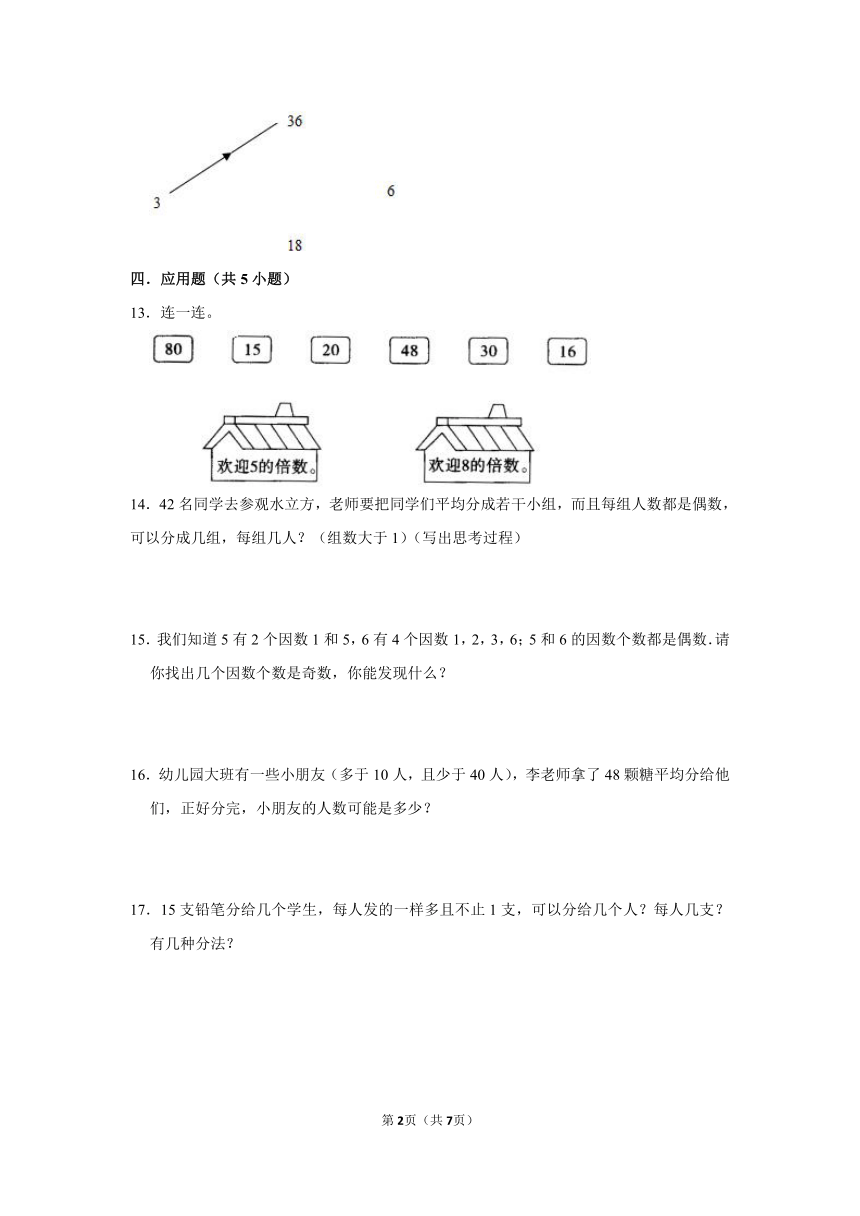
12.图中“”表示3是36的因数,用“”表示下面图中各数之间的关系.
四.应用题(共5小题)
13.连一连。
14.42名同学去参观水立方,老师要把同学们平均分成若干小组,而且每组人数都是偶数,可以分成几组,每组几人?(组数大于1)(写出思考过程)
15.我们知道5有2个因数1和5,6有4个因数1,2,3,6;5和6的因数个数都是偶数.请你找出几个因数个数是奇数,你能发现什么?
16.幼儿园大班有一些小朋友(多于10人,且少于40人),李老师拿了48颗糖平均分给他们,正好分完,小朋友的人数可能是多少?
17.15支铅笔分给几个学生,每人发的一样多且不止1支,可以分给几个人?每人几支?有几种分法?
同步作业 2.1因数与倍数 2021-2022学年下学期小学数学人教新版五年级
参考答案与试题解析
一.选择题(共6小题)
1.【分析】3的倍数的特点是各个数位上的和是3的倍数,先求出已知的3个数位的和,再看还差多少是3的倍数,即可求解.
【解答】解:3+5=8;
要使3□5是3的倍数,那么□里面可以填:
1,4,7;最大是7。
故选:A。
【点评】本题主要考查了3的倍数的特点:各个数位上的和是3的倍数。
2.【分析】既是奇数又是质数的数叫奇素数,要反映每一个大于4的偶数都可以表示成两个奇素数之和,一要看这个数是大于4的偶数,二是写成两个数的和中的每个加数必须都是奇素数,据此解答。
【解答】解:A.45=2+43,43是奇素数但2不是奇素数,故不符合题意;
B.40=11+29,11和29都是奇素数,故符合题意;
C.38=25+13,25和13都是奇数,但25不是质数,故不符合题意。
故选:B。
【点评】此题要反映这个猜想必须具备两个条件:一个数是大于4的偶数,并且表示出两个奇素数的和。
3.【分析】分别判断A,B,C,D中是否都是质数。然后锁定全部都是质数的选项。据此答题即可。
【解答】解:经分析得:
A.1不是质数;
B.9,51不是质数;
C.87不是质数;
D.全是质数。
故选:D。
【点评】本题考查质数合数的定义。结合定义判断质数即可解决问题。
4.【分析】一个数既是8的倍数,又是10的倍数,这个数是8和10的公倍数,找出8和10在50以内的公倍数即可。
【解答】解:8在50以内的倍数有:8,16,24,32,40,48;
10在50以内的倍数有:10,20,30,40,50;
8和10在50以内的公倍数是:40。
故选:C。
【点评】此题主要考查找两个数的公倍数的方法。
5.【分析】自然数中,除了1和它本身外还有别的因数的数为合数。由此可知,一个合数除了1和它本身外,至少还要有一个因数,即有两个以上因数。
【解答】解:根据合数的意义可知:
一个合数除了1和它本身外,至少还要有一个因数,即有两个以上因数。
故选:C。
【点评】本题重点考查了学生对于合数意义的理解。
6.【分析】写出40的所有因数和5在40以内的倍数,找出公有的,数出个数。
【解答】解:40的因数有:1,2,4,5,8,10,20,40;
5在40以内的倍数有:5,10,15,20,25,30,35,40;
既是40的因数又是5的倍数的数有:5,10,20,40,共4个。
故选:D。
【点评】解答此题关键在于能正确找出一个数的所有因数和找出一个数的倍数。
二.填空题(共5小题)
7.【分析】找配对的方法理解,12=1×12、2×6、3×4,那么,12的因数就有:1、2、3、4、6、12。奇数末尾有1,3,5,7,9的数,质数只有1和它本身这两个因数的数;合数是指除了1和它本身,还有其它因数的数就是合数,据此解答。
【解答】解:12的因数有 1、12、2、6、3、4 其中 1、3是奇数,2、3是质数,12、6、4是合数。
故答案为:1、12、2、6、3、4;1、3;2、3;12、6、4。
【点评】本题考查了求一个数因数的方法及奇数、质数、合数的特征。
8.【分析】合数:指自然数中除了能被1和本身整除外,还能被其他的数整除的数。“1”既不是质数也不是合数;质数:一个数只有1和它本身两个因数,这个数叫作质数;据此定义解答。
【解答】解:1既不是质数也不是合数。10以内的质数有2,3,5,7。
故答案为:1,2,3,5,7。
【点评】本题考查了质数和合数的认识。
9.【分析】根据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;进行解答即可。
【解答】解:45÷9=5,5和9是45的因数;45÷6=7......3,6不是45的因数,所以在在45、6和9中,9是45的因数。
故答案为:9,45。
【点评】此题考查了因数和倍数的意义,应明确因数和倍数的意义,注意基础知识的理解。
10.【分析】根据质数、合数的意义:一个自然数,如果只有1和它本身两个因数,这样的数叫做质数;一个自然数如果除了1和它本身还有别的因数,这样的数叫做合数,据此解答。
【解答】解:在1~20的自然数中,
质数有:2、3、5、7、11、13、17、19,最大的质数是19;
合数有:4、6、8、9、10、12、14、15、16、18、20,共11个。
故答案为:19,11。
【点评】此题考查的目的是理解质数、合数的意义,掌握20以内的质数。
11.【分析】根据奇数、偶数、质数和合数的意义:是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;一个自然数如果除了1和它本身还有其它的因数,那么这个自然数叫做合数,由此即可写出两个奇素数之和是100的素数。
【解答】解:100=3+97
100=89+11
故答案为:3+97(答案不唯一)。
【点评】此题考查的目的是理解奇数、偶数、质数和合数的意义,掌握奇数和质数的区别,偶数与合数的区别。
三.操作题(共1小题)
12.【分析】根据题意可知:3是36的因数,3是18的因数,3是6的因数,6是18的因数,6是36的因数,18是36的因数;进而用箭头画出即可.
【解答】解:如图,
【点评】此题考查了因数和倍数的意义.
四.应用题(共5小题)
13.【分析】利用求倍数的的方法求出5和8的倍数,再进行连线即可。
【解答】解:5的倍数:15、20、30;
8的倍数:16、48、80;
连线如下:
【点评】此题考查了找一个数的倍数的方法,应注意基础知识的积累。
14.【分析】写出两个整数的积等于42的所有乘法算式,偶数因数作每组人数,另一个因数作组数,组数不能为1。
【解答】解:两个整数的积等于42,偶数因数作每组人数,另一个因数作组数,组数不能为1。
1×42=42
偶数因数42作每组人数,组数为1,不符合题目组数大于1的要求。
2×21=42
3×14=42
6×7=42
答:可以分成21组,每组2人;
也可以分成3组,每组14人;
还可以分成7组,每组6人。
【点评】此题重点在于找出42的所有因数,并判断因数的奇偶性。
15.【分析】一个数的因数是成对出现的,要想因数个数是奇数个,就需有两个相同的因数,可举4和9,分析可得平方数的因数有奇数个.
【解答】解:4的因数有1,2,4,3个
9的因数有1,3,9,3个,
可得出平方数的因数有奇数个.
【点评】本题考查了找一个数的因数的方法,关键是分析出平方数的因数有奇数个.
16.【分析】根据因数与倍数的意义,和找一个数的因数的个数的方法,求出48的因数有哪些,根据题意可以平均分给多少个小朋友,由此解答。
【解答】解:48的因数有:1,2,3、4,6,8,12,16,24,48.
根据题意不可能分给1个小朋友,小朋友(多于10人,且少于40人),因此可以平均分给12,16,24个小朋友。
答:小朋友的人数可能是12,16,24。
【点评】此题主要考查求一个数的因数的方法,根据求一个数的因数的方法解决问题。
17.【分析】每人平均发的支数是15的大于1且小于15的因数,据此写出15的因数即可解决问题.
【解答】解:15的大于1且小于15的因数有:3、5,
所以,可以分给3个人,每人5支,或可以分给5个人,每人3支,共2种分法.
答:可以分给3个人,每人5支,或可以分给5个人,每人3支,共2种分法.
【点评】本题考查了找一个数的因数的方法的灵活应用,注意取值范围.
第6页(共7页)
一.选择题(共6小题)
1.要使3□5是3的倍数,方框里最大可以填( )
A.7 B.9 C.4
2.200多年前,德国数学家哥德巴赫发现:每一个大于4的偶数,都可以表示成两个奇素数之和。下面第( )个算式符合上面的发现。
A.45=2+43 B.40=11+29 C.38=25+13
3.下面几组数,全部都是质数的是( )
A.19,1,13 B.7,9,51 C.87,17,5 D.2,29,41
4.一个小于50的自然数,既是8的倍数,又是10的倍数,这个数是( )
A.8 B.10 C.40
5.合数的因数有( )
A.1个 B.3个 C.两个以上
6.一个数,既是40的因数又是5的倍数,这样的数有( )个。
A.1 B.2 C.3 D.4
二.填空题(共5小题)
7.12的因数有 其中 是奇数, 是质数, 是合数。
8. 既不是质数也不是合数。10以内的质数有 。
9.在45,6和9中, 是 的因数。
10.在1到20的自然数中,最大的质数是 ,共有 个合数。
11.“哥德巴赫猜想”认为,每个不小于6的偶数都可写成两个奇素数(既是奇数,又是质数)之和。如6=3+3,8=3+5,10=3+7=5+5,……100写成两个奇素数之和是 。
三.操作题(共1小题)
12.图中“”表示3是36的因数,用“”表示下面图中各数之间的关系.
四.应用题(共5小题)
13.连一连。
14.42名同学去参观水立方,老师要把同学们平均分成若干小组,而且每组人数都是偶数,可以分成几组,每组几人?(组数大于1)(写出思考过程)
15.我们知道5有2个因数1和5,6有4个因数1,2,3,6;5和6的因数个数都是偶数.请你找出几个因数个数是奇数,你能发现什么?
16.幼儿园大班有一些小朋友(多于10人,且少于40人),李老师拿了48颗糖平均分给他们,正好分完,小朋友的人数可能是多少?
17.15支铅笔分给几个学生,每人发的一样多且不止1支,可以分给几个人?每人几支?有几种分法?
同步作业 2.1因数与倍数 2021-2022学年下学期小学数学人教新版五年级
参考答案与试题解析
一.选择题(共6小题)
1.【分析】3的倍数的特点是各个数位上的和是3的倍数,先求出已知的3个数位的和,再看还差多少是3的倍数,即可求解.
【解答】解:3+5=8;
要使3□5是3的倍数,那么□里面可以填:
1,4,7;最大是7。
故选:A。
【点评】本题主要考查了3的倍数的特点:各个数位上的和是3的倍数。
2.【分析】既是奇数又是质数的数叫奇素数,要反映每一个大于4的偶数都可以表示成两个奇素数之和,一要看这个数是大于4的偶数,二是写成两个数的和中的每个加数必须都是奇素数,据此解答。
【解答】解:A.45=2+43,43是奇素数但2不是奇素数,故不符合题意;
B.40=11+29,11和29都是奇素数,故符合题意;
C.38=25+13,25和13都是奇数,但25不是质数,故不符合题意。
故选:B。
【点评】此题要反映这个猜想必须具备两个条件:一个数是大于4的偶数,并且表示出两个奇素数的和。
3.【分析】分别判断A,B,C,D中是否都是质数。然后锁定全部都是质数的选项。据此答题即可。
【解答】解:经分析得:
A.1不是质数;
B.9,51不是质数;
C.87不是质数;
D.全是质数。
故选:D。
【点评】本题考查质数合数的定义。结合定义判断质数即可解决问题。
4.【分析】一个数既是8的倍数,又是10的倍数,这个数是8和10的公倍数,找出8和10在50以内的公倍数即可。
【解答】解:8在50以内的倍数有:8,16,24,32,40,48;
10在50以内的倍数有:10,20,30,40,50;
8和10在50以内的公倍数是:40。
故选:C。
【点评】此题主要考查找两个数的公倍数的方法。
5.【分析】自然数中,除了1和它本身外还有别的因数的数为合数。由此可知,一个合数除了1和它本身外,至少还要有一个因数,即有两个以上因数。
【解答】解:根据合数的意义可知:
一个合数除了1和它本身外,至少还要有一个因数,即有两个以上因数。
故选:C。
【点评】本题重点考查了学生对于合数意义的理解。
6.【分析】写出40的所有因数和5在40以内的倍数,找出公有的,数出个数。
【解答】解:40的因数有:1,2,4,5,8,10,20,40;
5在40以内的倍数有:5,10,15,20,25,30,35,40;
既是40的因数又是5的倍数的数有:5,10,20,40,共4个。
故选:D。
【点评】解答此题关键在于能正确找出一个数的所有因数和找出一个数的倍数。
二.填空题(共5小题)
7.【分析】找配对的方法理解,12=1×12、2×6、3×4,那么,12的因数就有:1、2、3、4、6、12。奇数末尾有1,3,5,7,9的数,质数只有1和它本身这两个因数的数;合数是指除了1和它本身,还有其它因数的数就是合数,据此解答。
【解答】解:12的因数有 1、12、2、6、3、4 其中 1、3是奇数,2、3是质数,12、6、4是合数。
故答案为:1、12、2、6、3、4;1、3;2、3;12、6、4。
【点评】本题考查了求一个数因数的方法及奇数、质数、合数的特征。
8.【分析】合数:指自然数中除了能被1和本身整除外,还能被其他的数整除的数。“1”既不是质数也不是合数;质数:一个数只有1和它本身两个因数,这个数叫作质数;据此定义解答。
【解答】解:1既不是质数也不是合数。10以内的质数有2,3,5,7。
故答案为:1,2,3,5,7。
【点评】本题考查了质数和合数的认识。
9.【分析】根据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数;进行解答即可。
【解答】解:45÷9=5,5和9是45的因数;45÷6=7......3,6不是45的因数,所以在在45、6和9中,9是45的因数。
故答案为:9,45。
【点评】此题考查了因数和倍数的意义,应明确因数和倍数的意义,注意基础知识的理解。
10.【分析】根据质数、合数的意义:一个自然数,如果只有1和它本身两个因数,这样的数叫做质数;一个自然数如果除了1和它本身还有别的因数,这样的数叫做合数,据此解答。
【解答】解:在1~20的自然数中,
质数有:2、3、5、7、11、13、17、19,最大的质数是19;
合数有:4、6、8、9、10、12、14、15、16、18、20,共11个。
故答案为:19,11。
【点评】此题考查的目的是理解质数、合数的意义,掌握20以内的质数。
11.【分析】根据奇数、偶数、质数和合数的意义:是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;一个自然数如果除了1和它本身还有其它的因数,那么这个自然数叫做合数,由此即可写出两个奇素数之和是100的素数。
【解答】解:100=3+97
100=89+11
故答案为:3+97(答案不唯一)。
【点评】此题考查的目的是理解奇数、偶数、质数和合数的意义,掌握奇数和质数的区别,偶数与合数的区别。
三.操作题(共1小题)
12.【分析】根据题意可知:3是36的因数,3是18的因数,3是6的因数,6是18的因数,6是36的因数,18是36的因数;进而用箭头画出即可.
【解答】解:如图,
【点评】此题考查了因数和倍数的意义.
四.应用题(共5小题)
13.【分析】利用求倍数的的方法求出5和8的倍数,再进行连线即可。
【解答】解:5的倍数:15、20、30;
8的倍数:16、48、80;
连线如下:
【点评】此题考查了找一个数的倍数的方法,应注意基础知识的积累。
14.【分析】写出两个整数的积等于42的所有乘法算式,偶数因数作每组人数,另一个因数作组数,组数不能为1。
【解答】解:两个整数的积等于42,偶数因数作每组人数,另一个因数作组数,组数不能为1。
1×42=42
偶数因数42作每组人数,组数为1,不符合题目组数大于1的要求。
2×21=42
3×14=42
6×7=42
答:可以分成21组,每组2人;
也可以分成3组,每组14人;
还可以分成7组,每组6人。
【点评】此题重点在于找出42的所有因数,并判断因数的奇偶性。
15.【分析】一个数的因数是成对出现的,要想因数个数是奇数个,就需有两个相同的因数,可举4和9,分析可得平方数的因数有奇数个.
【解答】解:4的因数有1,2,4,3个
9的因数有1,3,9,3个,
可得出平方数的因数有奇数个.
【点评】本题考查了找一个数的因数的方法,关键是分析出平方数的因数有奇数个.
16.【分析】根据因数与倍数的意义,和找一个数的因数的个数的方法,求出48的因数有哪些,根据题意可以平均分给多少个小朋友,由此解答。
【解答】解:48的因数有:1,2,3、4,6,8,12,16,24,48.
根据题意不可能分给1个小朋友,小朋友(多于10人,且少于40人),因此可以平均分给12,16,24个小朋友。
答:小朋友的人数可能是12,16,24。
【点评】此题主要考查求一个数的因数的方法,根据求一个数的因数的方法解决问题。
17.【分析】每人平均发的支数是15的大于1且小于15的因数,据此写出15的因数即可解决问题.
【解答】解:15的大于1且小于15的因数有:3、5,
所以,可以分给3个人,每人5支,或可以分给5个人,每人3支,共2种分法.
答:可以分给3个人,每人5支,或可以分给5个人,每人3支,共2种分法.
【点评】本题考查了找一个数的因数的方法的灵活应用,注意取值范围.
第6页(共7页)
