指数与指数幂的运算
图片预览









文档简介
课件37张PPT。2.1.1指数与指数幂的运算(一) 银杏,叶子夏绿秋黄,是全球中最古老的树种.在200多万年前,第四纪冰川出现,大部分地区的银杏毁于一旦,残留的遗体成为了印在石头里的植物化石.在这场大灾难中,只有中国保存了一部分活的银杏树,绵延至今,成了研究古代银杏的活教材.所以,人们把它称为“世界第一活化石”. 考古学家根据什么推断出银杏于200多万年前就存在呢?创设情景问题:当生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据此规律,人们获得了生物体内含量P与死亡年数t之间的关系,这个关系式应该怎样表示呢我们可以先来考虑这样的问题:(1)当生物体死亡了5730, 5730×2, 5730×3,…年后,它体内碳14的含量P分别为原来的多少?创设情景正整数指数幂的含义是 。 正整数指数幂的运算性质是:
(1) ;
(2) ;
(3) 。(2)当生物体死亡了6000年,10000年,100000年后,它体内碳14的含量P分别为原来的多少?(3)由以上的实例来推断关系式应该是什么? 考古学家根据上式可以知道, 生物死亡t年后,体内碳14的含量P的值.创设情景(4)那么这些数 的意义究竟是什么呢?它和我们初中所学的指数有什么区别?这里的指数是分数的形式. 指数可以取分数吗?除了分数还可以取其它的数吗?我们对于数的认识规律是怎样的?自然数→整数→分数(有理数)→实数.创设情景
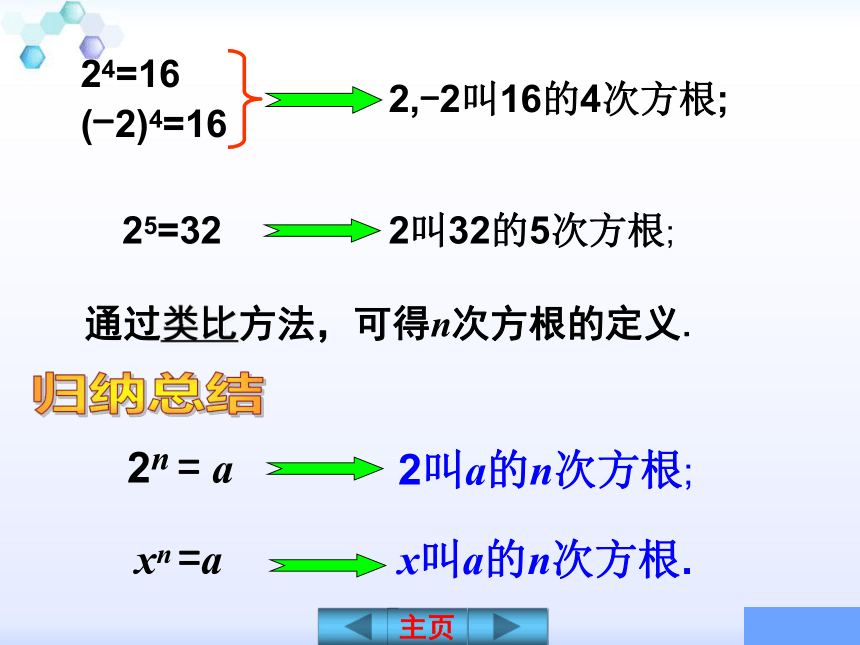
22=4
(-2)2=4(一)探求n次方根的概念 回顾初中知识,根式是如何定义的?有那些规定?①如果一个数的平方等于a,则这个数叫做 a的平方根.②如果一个数的立方等于a,则这个数叫做a 的立方根.2,-2叫4的平方根.2叫8的立方根.-2叫-8的立方根.23=8(-2)3=-8构建数学24=16
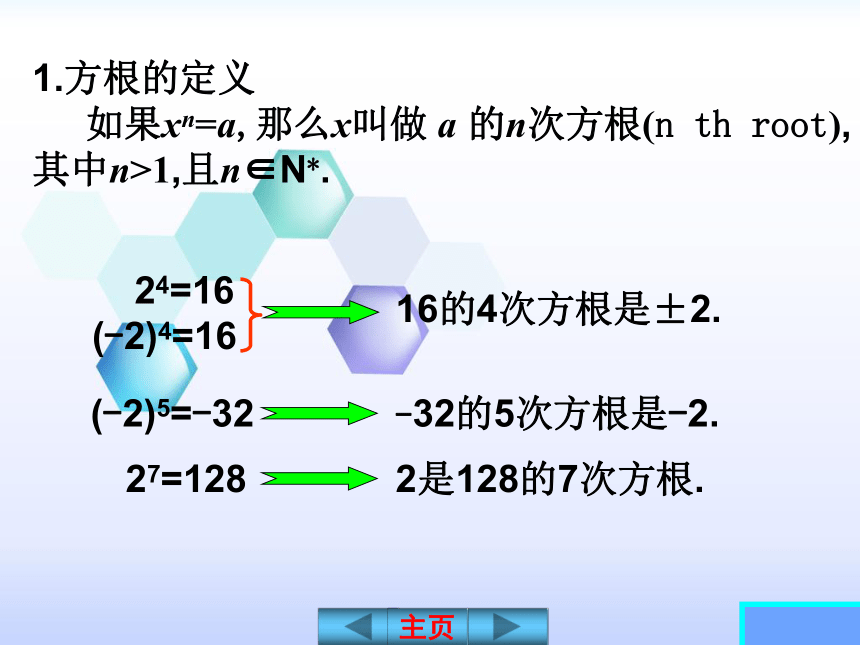
(-2)4=162,-2叫16的4次方根;2叫32的5次方根;2叫a的n次方根;x叫a的n次方根.xn =a2n = a25=32归纳总结通过类比方法,可得n次方根的定义.1.方根的定义
如果xn=a,那么x叫做 a 的n次方根(n th root), 其中n>1,且n∈N*. 24=16
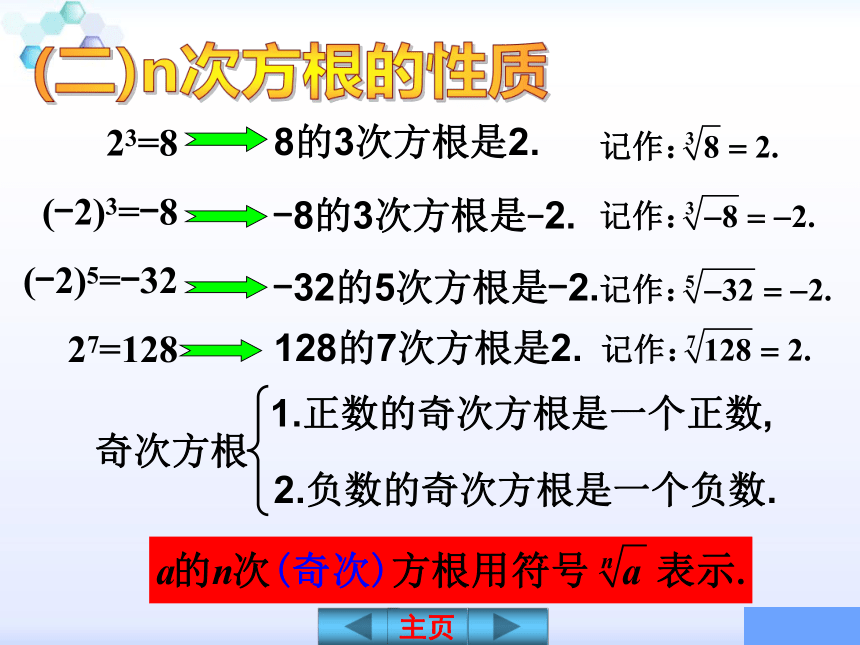
(-2)4=1616的4次方根是±2.(-2)5=-32-32的5次方根是-2.2是128的7次方根.27=128概念理解 【1】试根据n次方根的定义分别求出下列各数的n次方根.(1)25的平方根是_______;(2)27的三次方根是_____;(3)-32的五次方根是____;(4)16的四次方根是_____;(5)a6的三次方根是_____;(6)0的七次方根是______.点评:求一个数a的n次方根就是求出哪个数的n次方等于a.±53-2±20a223=8
(-2)3=-8
(-2)5=-32
27=1288的3次方根是2.-8的3次方根是-2.-32的5次方根是-2.128的7次方根是2.奇次方根 1.正数的奇次方根是一个正数, 2.负数的奇次方根是一个负数.(二)n次方根的性质72=49
(-7)2=49
34=81
(-3)4=8149的2次方根是7,-7.81的4次方根是3,-3.偶次方根 2.负数的偶次方根没有意义 1.正数的偶次方根有两个且互为相反数 26=64
(-2)6=6464的6次方根是2,-2.正数的奇次方根是正数.
负数的奇次方根是负数.
零的奇次方根是零.(二)n次方根的性质(1) 奇次方根有以下性质:(2)偶次方根有以下性质:正数的偶次方根有两个且是相反数,
负数没有偶次方根,
零的偶次方根是零. 根指数根式(三)根式的概念被开方数 由xn = a 可知,x叫做a的n次方根.9-8归纳总结1 当n是奇数时, 对任意a?R都有意义.它表示a在实数范围内唯一的一个n次方根. 当n是偶数时, 只有当a≥0有意义,当a<0时无意义. 表示a在实数范围内的一个n次方根,另一个是归纳总结2式子 对任意a ? R都有意义.结论:an开奇次方根,则有结论:an开偶次方根,则有公式1.(四)n次方根的运算性质适用范围:①当n为大于1的奇数时, a∈R.②当n为大于1的偶数时, a≥0.公式2.适用范围:n为大于1的奇数, a∈R.公式3.适用范围:n为大于1的偶数, a∈R.= -8;=10;例1.求下列各式的值数学运用(1) 下列说法正确的是_____.
①正数的偶次方根是一个正数;②正数的奇次方根是一个正数;③负数的偶次方根是一个负数;④负数的奇次方根是一个负数.
【规范解答】由n次方根的概念可知,正数的奇次方根是一个正数,负数的奇次方根是一个负数,正数的偶次方根有两个,负数没有偶次方根,故②④正确.
答案:②④① ④【2】下列各式中, 不正确的序号是( ).练一练解:练一练【3】求下列各式的值.例2.填空: (1)在
这四个式子中,没有意义的是________. (2) 若 则a 的取值范围是______. (3)已知a, b, c为三角形的三边,则1.以下选项正确的是( )
【解析】选B.当a1,n∈N*,化简
【解析】∵a<b<0∴a-b<0且a+b<0
当n是奇数时,原式=a-b+a+b=2a,
当n是偶数时,
原式=|a-b|+|a+b|=b-a-(a+b)=-2a.
综上,3.若 有意义,则实数a的取值范围是_____.
【解析】由n次方根的定义可知a-3≠0,即a≠3.
答案:a≠34.若 有意义,则实数x的取值范围为_____.
【解析】因为负数没有偶次方根,
所以x-1≥0,即x≥1.
答案:x≥1( )6.(10分)化简
【解题提示】本题有偶次方根,暗含了被开方数非负,可求得a的范围,再利用n次方根的性质求解.
【解析】由题意可知 有意义,所以a≥1.
原式=(a-1)+|1-a|+a-1
=a-1+a-1+a-1=3a-3.8. =_____.
【解析】
答案:9.若 实数x满足的条件为( )
(A)x>4 (B)x<4 (C)x≤4 (D)x≥4
【解析】选D. =|x-4|=x-4,
所以x-4≥0,即x≥4.例 化简
【思路点拨】解答本题可先把根号内的小括号展开,进行整理后化成完全平方的形式再进行化简.
【规范解答】
=π-π-1+π+π-1=2π.例3 设-3因为-3当-3当1≤x<3时,原式=(x-1)-(x+3)=-4.
所以,原式解:数学运用例1.求值: 例2.如果 化简代数式解:解之,得所以例3.计算 解:则有所以x的取值范围是2.根式的性质
(1)当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时,a的n次方根用符号 表示.1.根式定义(2)当n为偶数时,正数a的n次方根有两个, 合写为负数没有偶次方根.零的任何次方根都是零. 零的任何次方根都是零. 课堂小结4.若xn=a , x怎样用a表示?3.三个公式课堂小结
(1) ;
(2) ;
(3) 。(2)当生物体死亡了6000年,10000年,100000年后,它体内碳14的含量P分别为原来的多少?(3)由以上的实例来推断关系式应该是什么? 考古学家根据上式可以知道, 生物死亡t年后,体内碳14的含量P的值.创设情景(4)那么这些数 的意义究竟是什么呢?它和我们初中所学的指数有什么区别?这里的指数是分数的形式. 指数可以取分数吗?除了分数还可以取其它的数吗?我们对于数的认识规律是怎样的?自然数→整数→分数(有理数)→实数.创设情景
22=4
(-2)2=4(一)探求n次方根的概念 回顾初中知识,根式是如何定义的?有那些规定?①如果一个数的平方等于a,则这个数叫做 a的平方根.②如果一个数的立方等于a,则这个数叫做a 的立方根.2,-2叫4的平方根.2叫8的立方根.-2叫-8的立方根.23=8(-2)3=-8构建数学24=16
(-2)4=162,-2叫16的4次方根;2叫32的5次方根;2叫a的n次方根;x叫a的n次方根.xn =a2n = a25=32归纳总结通过类比方法,可得n次方根的定义.1.方根的定义
如果xn=a,那么x叫做 a 的n次方根(n th root), 其中n>1,且n∈N*. 24=16
(-2)4=1616的4次方根是±2.(-2)5=-32-32的5次方根是-2.2是128的7次方根.27=128概念理解 【1】试根据n次方根的定义分别求出下列各数的n次方根.(1)25的平方根是_______;(2)27的三次方根是_____;(3)-32的五次方根是____;(4)16的四次方根是_____;(5)a6的三次方根是_____;(6)0的七次方根是______.点评:求一个数a的n次方根就是求出哪个数的n次方等于a.±53-2±20a223=8
(-2)3=-8
(-2)5=-32
27=1288的3次方根是2.-8的3次方根是-2.-32的5次方根是-2.128的7次方根是2.奇次方根 1.正数的奇次方根是一个正数, 2.负数的奇次方根是一个负数.(二)n次方根的性质72=49
(-7)2=49
34=81
(-3)4=8149的2次方根是7,-7.81的4次方根是3,-3.偶次方根 2.负数的偶次方根没有意义 1.正数的偶次方根有两个且互为相反数 26=64
(-2)6=6464的6次方根是2,-2.正数的奇次方根是正数.
负数的奇次方根是负数.
零的奇次方根是零.(二)n次方根的性质(1) 奇次方根有以下性质:(2)偶次方根有以下性质:正数的偶次方根有两个且是相反数,
负数没有偶次方根,
零的偶次方根是零. 根指数根式(三)根式的概念被开方数 由xn = a 可知,x叫做a的n次方根.9-8归纳总结1 当n是奇数时, 对任意a?R都有意义.它表示a在实数范围内唯一的一个n次方根. 当n是偶数时, 只有当a≥0有意义,当a<0时无意义. 表示a在实数范围内的一个n次方根,另一个是归纳总结2式子 对任意a ? R都有意义.结论:an开奇次方根,则有结论:an开偶次方根,则有公式1.(四)n次方根的运算性质适用范围:①当n为大于1的奇数时, a∈R.②当n为大于1的偶数时, a≥0.公式2.适用范围:n为大于1的奇数, a∈R.公式3.适用范围:n为大于1的偶数, a∈R.= -8;=10;例1.求下列各式的值数学运用(1) 下列说法正确的是_____.
①正数的偶次方根是一个正数;②正数的奇次方根是一个正数;③负数的偶次方根是一个负数;④负数的奇次方根是一个负数.
【规范解答】由n次方根的概念可知,正数的奇次方根是一个正数,负数的奇次方根是一个负数,正数的偶次方根有两个,负数没有偶次方根,故②④正确.
答案:②④① ④【2】下列各式中, 不正确的序号是( ).练一练解:练一练【3】求下列各式的值.例2.填空: (1)在
这四个式子中,没有意义的是________. (2) 若 则a 的取值范围是______. (3)已知a, b, c为三角形的三边,则1.以下选项正确的是( )
【解析】选B.当a
【解析】∵a<b<0∴a-b<0且a+b<0
当n是奇数时,原式=a-b+a+b=2a,
当n是偶数时,
原式=|a-b|+|a+b|=b-a-(a+b)=-2a.
综上,3.若 有意义,则实数a的取值范围是_____.
【解析】由n次方根的定义可知a-3≠0,即a≠3.
答案:a≠34.若 有意义,则实数x的取值范围为_____.
【解析】因为负数没有偶次方根,
所以x-1≥0,即x≥1.
答案:x≥1( )6.(10分)化简
【解题提示】本题有偶次方根,暗含了被开方数非负,可求得a的范围,再利用n次方根的性质求解.
【解析】由题意可知 有意义,所以a≥1.
原式=(a-1)+|1-a|+a-1
=a-1+a-1+a-1=3a-3.8. =_____.
【解析】
答案:9.若 实数x满足的条件为( )
(A)x>4 (B)x<4 (C)x≤4 (D)x≥4
【解析】选D. =|x-4|=x-4,
所以x-4≥0,即x≥4.例 化简
【思路点拨】解答本题可先把根号内的小括号展开,进行整理后化成完全平方的形式再进行化简.
【规范解答】
=π-π-1+π+π-1=2π.例3 设-3
所以,原式解:数学运用例1.求值: 例2.如果 化简代数式解:解之,得所以例3.计算 解:则有所以x的取值范围是2.根式的性质
(1)当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时,a的n次方根用符号 表示.1.根式定义(2)当n为偶数时,正数a的n次方根有两个, 合写为负数没有偶次方根.零的任何次方根都是零. 零的任何次方根都是零. 课堂小结4.若xn=a , x怎样用a表示?3.三个公式课堂小结
