2021—2022学年北师大版七年级数学上册1.1生活中的立体图形同步练习(Word版,附答案)
文档属性
| 名称 | 2021—2022学年北师大版七年级数学上册1.1生活中的立体图形同步练习(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 292.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 23:47:37 | ||
图片预览


文档简介
北师大版数学七年级上同步练习:1.1生活中的立体图形
一、选择题
四棱柱的顶点数、棱数、面数分别是
A. ,, B. ,, C. ,, D. ,,
下列说法中,正确的个数是
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A. 个 B. 个 C. 个 D. 个
下列图形,不是柱体的是
A. B. C. D.
将半圆绕它的直径旋转一周形成的几何体是
A.圆柱 B.圆锥 C.球 D.正方体
一个四棱柱的面共有
A. 个 B. 个 C. 个 D. 个
如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有 条棱.下列棱柱中和九棱锥的棱数相等的是
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
下列图形:①长方体;②三角形;③点;④直线;⑤圆柱;⑥球;⑦圆;⑧平行四边形.其中为平面图形的有
A. 个 B. 个 C. 个 D. 个
用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为
①正方体;
②圆柱;
③圆锥;
④正三棱柱.
A.①②③④ B.①③④ C.①④ D.①②
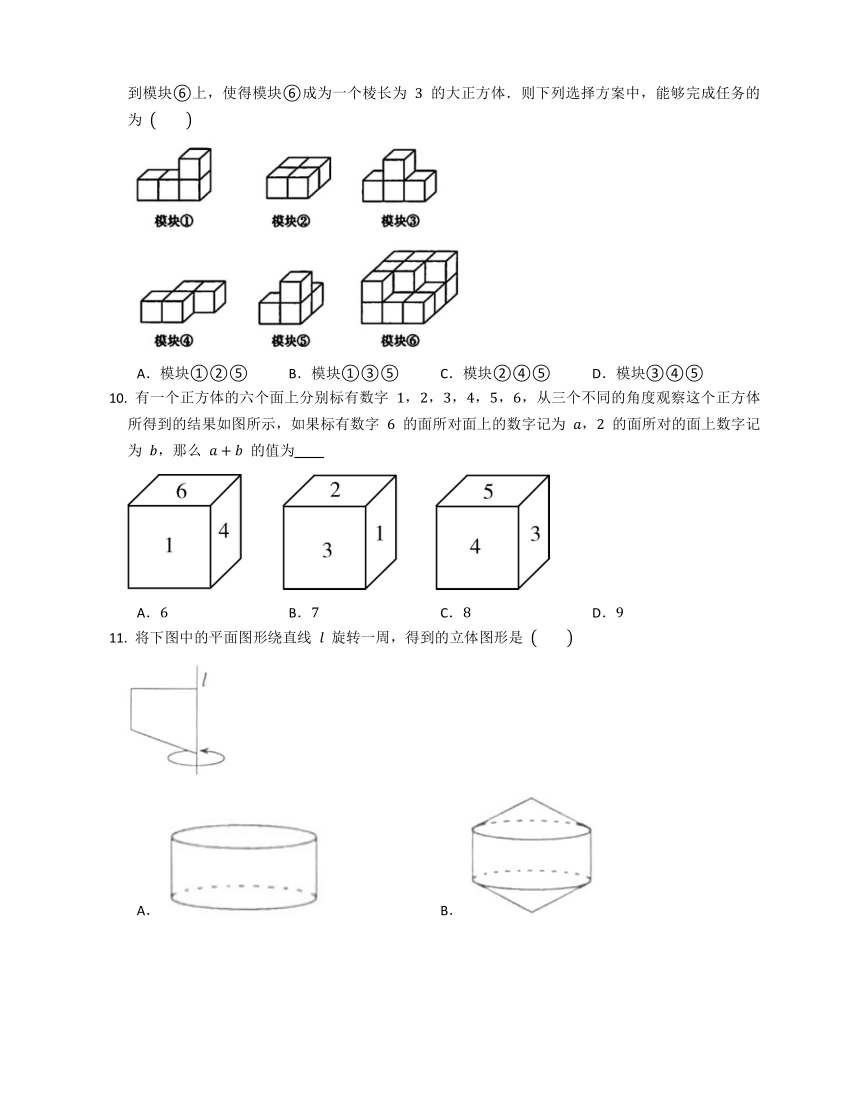
小明在玩堆积木的游戏,他的妈妈为他出了如下这道题:如图,模块① ⑤均由 个棱长为 的小正方体构成,模块⑥由 个棱长为 的小正方体构成.现从模块① ⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为 的大正方体.则下列选择方案中,能够完成任务的为
A.模块①②⑤ B.模块①③⑤ C.模块②④⑤ D.模块③④⑤
有一个正方体的六个面上分别标有数字 ,,,,,,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字 的面所对面上的数字记为 , 的面所对的面上数字记为 ,那么 的值为
A. B. C. D.
将下图中的平面图形绕直线 旋转一周,得到的立体图形是
A. B.
C. D.
图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体应是
A. B. C. D.
七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那幅图是
A.
B.
C.
D.
二、填空题
如图所示为 个立体图形.
其中,柱体的序号为 ,锥体的序号为 ,有曲面的序号为 .
下面各图中,是平面图形的有 ;是立体图形的有 .
如图,用一个平面截去正方体一角,变成一个新的多面体,这个新多面体有 个面,有 条棱,有 个顶点,截去的几何体有 个面.
一个直五棱柱,它的底面的边长都相等,侧棱长 ,且这个五棱柱的所有侧面的面积和为 ,则这个五棱柱的上底面周长为 .
如图,一个 的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则所得几何体的体积为 .
三、解答题
你能找出柱体、锥体、球体这几种常见的几何体的特点吗?
观察如图所示的几何体,回答下列问题.
(1) 填写下表:
(2) 由此可推测 ( 为大于或等于 的正整数)棱柱有多少个面?多少个顶点?多少条棱?
如图所示的立体图形的表面分别包含哪些平面图形?并分别指出这些平面图形在立体图形中的位置.
如图所示,图① ④都是平面图形.
(1) 每个图中各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入表格中.
4 6 3
(2) 根据表中数值,若具有相同规律的平面图形顶点数为 ( 为不小于 的偶数),可推断出区域数为 ;边数为 .
答案
一、选择题
1.A 2.B 3.D 4.C 5.D 6.B 7.B 8.B 9.A 10.B 11.D 12.B 13.C
二、填空题
14.①②⑤⑦;④⑥;①③④
15.①④⑤;②③⑥
16. ; ;
17.
18.
三、解答题
19. .柱体.
()正方体:它有 个顶点, 条棱, 个面,其中 条棱长都相等, 个面都是相同的正方形.
()长方体:它有 个顶点, 条棱, 个面,其中各个面都是长方形,且相对的两个面大小相等.
()棱柱:图①、图②中的上、下两个面叫做棱柱的底面,周围的面叫做棱柱的侧面,面与面的交线是棱柱的棱,其中侧面与侧面的交线是侧棱,棱与棱的交点是顶点.
正方体和长方体是特殊的棱柱,它们都是四棱柱.正方体是特殊的长方体.
()圆柱:图③中的上、下两个圆面是圆柱的底面,这两个底面是半径相同的圆,周围是圆柱的侧面.棱柱和圆柱统称柱体.
.锥体.
()圆锥:图④中的圆面是圆锥的底面,曲面是圆锥的侧面,圆锥还有一个顶点.
()棱锥:图⑤中下面的多边形面是棱锥的底面,其余各三角形面是棱锥的侧面,各侧面的交线是棱锥的侧棱,各侧棱的交点是棱锥的顶点.棱锥和圆锥统称锥体.
.球体.
球体是半圆绕其直径旋转而成的几何体,如篮球、足球等都是球体.
20.(1) ;;;;
;;;;
;;;
(2) 棱柱有 个面, 个顶点, 条棱.
21.该四棱锥表面有 个平面图形,其中侧面是 个三角形,底面是 个长方形.
22.(1)
(2) ;
一、选择题
四棱柱的顶点数、棱数、面数分别是
A. ,, B. ,, C. ,, D. ,,
下列说法中,正确的个数是
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A. 个 B. 个 C. 个 D. 个
下列图形,不是柱体的是
A. B. C. D.
将半圆绕它的直径旋转一周形成的几何体是
A.圆柱 B.圆锥 C.球 D.正方体
一个四棱柱的面共有
A. 个 B. 个 C. 个 D. 个
如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有 条棱.下列棱柱中和九棱锥的棱数相等的是
A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
下列图形:①长方体;②三角形;③点;④直线;⑤圆柱;⑥球;⑦圆;⑧平行四边形.其中为平面图形的有
A. 个 B. 个 C. 个 D. 个
用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为
①正方体;
②圆柱;
③圆锥;
④正三棱柱.
A.①②③④ B.①③④ C.①④ D.①②
小明在玩堆积木的游戏,他的妈妈为他出了如下这道题:如图,模块① ⑤均由 个棱长为 的小正方体构成,模块⑥由 个棱长为 的小正方体构成.现从模块① ⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为 的大正方体.则下列选择方案中,能够完成任务的为
A.模块①②⑤ B.模块①③⑤ C.模块②④⑤ D.模块③④⑤
有一个正方体的六个面上分别标有数字 ,,,,,,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字 的面所对面上的数字记为 , 的面所对的面上数字记为 ,那么 的值为
A. B. C. D.
将下图中的平面图形绕直线 旋转一周,得到的立体图形是
A. B.
C. D.
图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体应是
A. B. C. D.
七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那幅图是
A.
B.
C.
D.
二、填空题
如图所示为 个立体图形.
其中,柱体的序号为 ,锥体的序号为 ,有曲面的序号为 .
下面各图中,是平面图形的有 ;是立体图形的有 .
如图,用一个平面截去正方体一角,变成一个新的多面体,这个新多面体有 个面,有 条棱,有 个顶点,截去的几何体有 个面.
一个直五棱柱,它的底面的边长都相等,侧棱长 ,且这个五棱柱的所有侧面的面积和为 ,则这个五棱柱的上底面周长为 .
如图,一个 的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则所得几何体的体积为 .
三、解答题
你能找出柱体、锥体、球体这几种常见的几何体的特点吗?
观察如图所示的几何体,回答下列问题.
(1) 填写下表:
(2) 由此可推测 ( 为大于或等于 的正整数)棱柱有多少个面?多少个顶点?多少条棱?
如图所示的立体图形的表面分别包含哪些平面图形?并分别指出这些平面图形在立体图形中的位置.
如图所示,图① ④都是平面图形.
(1) 每个图中各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入表格中.
4 6 3
(2) 根据表中数值,若具有相同规律的平面图形顶点数为 ( 为不小于 的偶数),可推断出区域数为 ;边数为 .
答案
一、选择题
1.A 2.B 3.D 4.C 5.D 6.B 7.B 8.B 9.A 10.B 11.D 12.B 13.C
二、填空题
14.①②⑤⑦;④⑥;①③④
15.①④⑤;②③⑥
16. ; ;
17.
18.
三、解答题
19. .柱体.
()正方体:它有 个顶点, 条棱, 个面,其中 条棱长都相等, 个面都是相同的正方形.
()长方体:它有 个顶点, 条棱, 个面,其中各个面都是长方形,且相对的两个面大小相等.
()棱柱:图①、图②中的上、下两个面叫做棱柱的底面,周围的面叫做棱柱的侧面,面与面的交线是棱柱的棱,其中侧面与侧面的交线是侧棱,棱与棱的交点是顶点.
正方体和长方体是特殊的棱柱,它们都是四棱柱.正方体是特殊的长方体.
()圆柱:图③中的上、下两个圆面是圆柱的底面,这两个底面是半径相同的圆,周围是圆柱的侧面.棱柱和圆柱统称柱体.
.锥体.
()圆锥:图④中的圆面是圆锥的底面,曲面是圆锥的侧面,圆锥还有一个顶点.
()棱锥:图⑤中下面的多边形面是棱锥的底面,其余各三角形面是棱锥的侧面,各侧面的交线是棱锥的侧棱,各侧棱的交点是棱锥的顶点.棱锥和圆锥统称锥体.
.球体.
球体是半圆绕其直径旋转而成的几何体,如篮球、足球等都是球体.
20.(1) ;;;;
;;;;
;;;
(2) 棱柱有 个面, 个顶点, 条棱.
21.该四棱锥表面有 个平面图形,其中侧面是 个三角形,底面是 个长方形.
22.(1)
(2) ;
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
