2021-2022学年北师大版九年级数学下册3.9弧长及扇形面积分类训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.9弧长及扇形面积分类训练 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 223.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 09:14:55 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3-9弧长及扇形面积》知识点分类训练(附答案)
一.弧长的计算
1.如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )
A.2+ B.+ C.+ D.2+
2.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )
A.1个 B.2个 C.3个 D.4个
3.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .
4.已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则所得到的三条弧的长度之和为 cm(结果保留π).
5.如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则凸轮的周长等于 .
6.如图,在△ABC中,∠A=70°,BC=4,以BC的中点D为圆心,2为半径作弧,分别交边AB、AC于E、F,则的长为 .
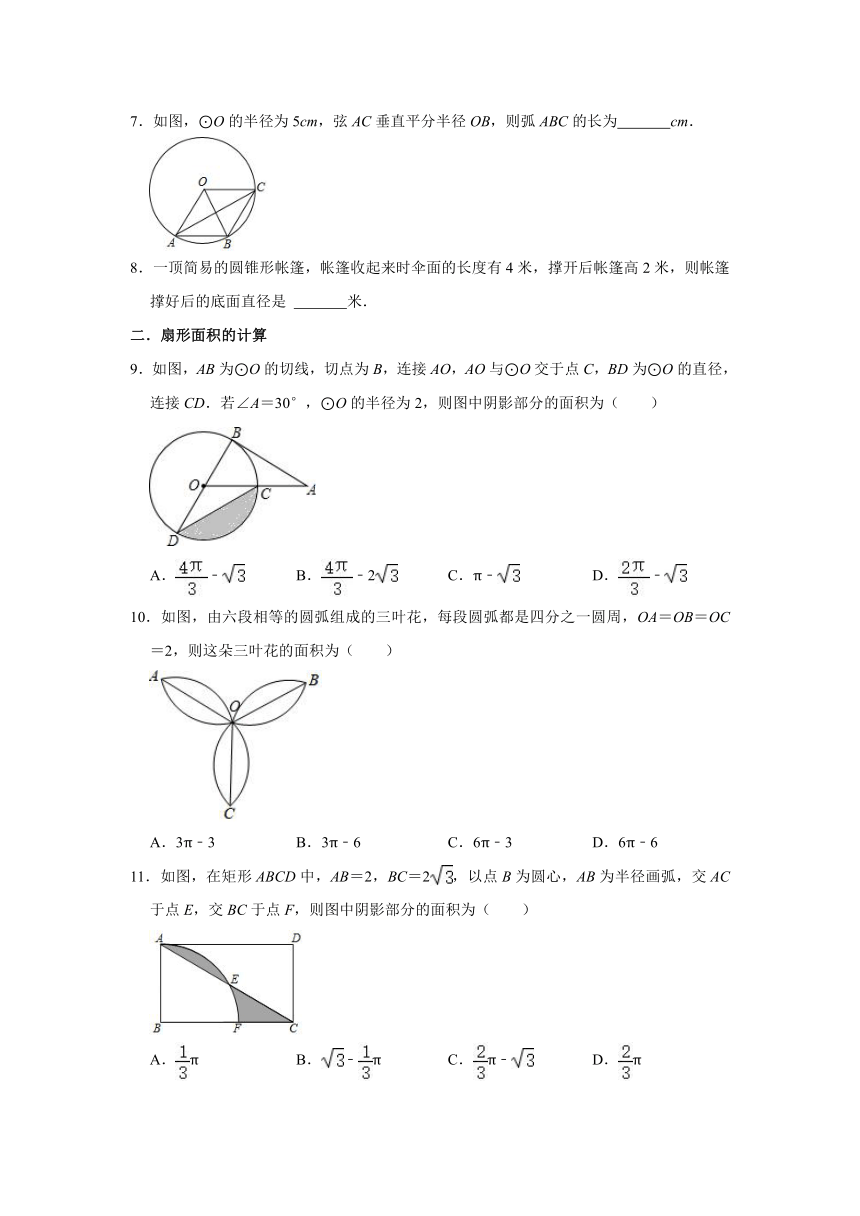
7.如图,⊙O的半径为5cm,弦AC垂直平分半径OB,则弧ABC的长为 cm.
8.一顶简易的圆锥形帐篷,帐篷收起来时伞面的长度有4米,撑开后帐篷高2米,则帐篷撑好后的底面直径是 米.
二.扇形面积的计算
9.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.﹣ B.﹣2 C.π﹣ D.﹣
10.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA=OB=OC=2,则这朵三叶花的面积为( )
A.3π﹣3 B.3π﹣6 C.6π﹣3 D.6π﹣6
11.如图,在矩形ABCD中,AB=2,BC=2,以点B为圆心,AB为半径画弧,交AC于点E,交BC于点F,则图中阴影部分的面积为( )
A.π B.﹣π C.π﹣ D.π
12.如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )
A.π B.2π C.3π D.4π
13.一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是 cm2.
14.如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π) .
15.如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为cm,弦CD的长为3cm,则图中阴影部分面积是 .
16.如图,扇形AOB的圆心角为直角,边长为1的正方形OCDE的顶点C,E,D分别在OA,OB,上,过点A作AF⊥ED,交ED的延长线于点F,则图中阴影部分的面积等于 .
17.如图,在⊙O中,OA=2,∠C=45°,则图中阴影部分的面积为 .
18.如图,AB是半径为6的⊙O的直径,CD是弦,且AB⊥CD于E,若∠COD=60°,则图中阴影部分的面积是 .
19.已知扇形的圆心角为60°,半径为3,则该扇形的弧长为 ,面积为 .
20.已知扇形的圆心角为45°,半径长为12,则该扇形的面积为 .
21.如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.
(1)求∠AOC的度数;
(2)若⊙O的半径为3,求图中阴影部分的面积.
22.已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
23.已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
(1)求∠DAB的度数;
(2)求图中阴影部分的面积(结果保留π).
参考答案
一.弧长的计算
1.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长l==,
∴阴影部分周长的最小值为2+.
故选:D.
2.解:①优弧比劣弧长,不一定,在同圆或等圆中结论成立,故①错误.
②三点可以确定一个圆,错误,应该是过不在同一直线上的三个点确定一个圆.故②错误.
③长度相等的弧是等弧,错误,长度相等的弧不一定相等,等弧的长度相等,故③错误.
④经过圆内的一个定点可以作无数条弦,故④正确.
故选:C.
3.解:,解得r=.
故答案为:.
4.解:方法一:
先求出正六边形的每一个内角=,
所得到的三条弧的长度之和=3×=2πcm;
方法二:先求出正六边形的每一个外角为60°,
得正六边形的每一个内角120°,
每条弧的度数为120°,
三条弧可拼成一整圆,其三条弧的长度之和为2πcm.
故答案为:2π.
5.
解:∵△ABC为正三角形,
∴∠A=∠B=∠C=60°,AB=AC=BC=1,
∴====,
根据题意可知凸轮的周长为三个弧长的和,
即凸轮的周长=++=3×=π.
故答案为:π
6.解:由题意,DB=DE=DF=2,
∴∠B=∠DEB,∠C=∠DFC,
∵∠A=70°,
∴∠B+∠C=110°,
∴∠BDE+∠CDF=360°﹣2(∠B+∠C)=140°,
∴∠EDF=180°﹣140°=40°,
∴的长==π,
故答案为:π.
7.解:∵弦AC垂直平分半径OB,
∴AO=AB,CO=CB,
∴OA=AB=OB=OC=BC,
∴△OAB和△OBC都是等边三角形,
∴∠AOB=∠COB=60°,
∴∠AOC=120°,
∴弧ABC的长==π(cm).
故答案为π.
8.解:r===2,
直径为4米.
二.扇形面积的计算
9.解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:﹣×2×1=π﹣.
故选:A.
10.解:如图所示:弧OA是⊙M上满足条件的一段弧,连接AM、MO,
由题意知:∠AMO=90°,AM=OM
∵AO=2,∴AM=.
∵S扇形AMO=×π×MA2=.
S△AMO=AM MO=1,
∴S弓形AO=﹣1,
∴S三叶花=6×(﹣1)
=3π﹣6.
故选:B.
11.解:连接BE,过E作EH⊥BC于H,
在矩形ABCD中,∵∠ABC=90°,AB=2,BC=2,
∴tan∠BAC==,
∴∠BAC=60°,
∵BA=BE,
∴△ABE是等边三角形,
∴∠ABE=60°,
∴∠EBH=30°,
∴EH=BE=1,
∴S阴=S扇形BAE+S△BCE﹣S△ABE﹣S扇形BEF=+﹣﹣=,
故选:A.
12.解:根据三角形的外角和是360°以及扇形的面积公式,得阴影部分的面积和是:=4π.
故选:D.
13.解:设扇形的半径为Rcm,
∵扇形的圆心角为135°,弧长为3πcm,
∴=3π,
解得:R=4,
所以此扇形的面积为=6π(cm2),
故答案为:6π.
14.解:连接AD,OD,
∵等腰直角△ABC中,
∴∠ABD=45°.
∵AB是圆的直径,
∴∠ADB=90°,
∴△ABD也是等腰直角三角形,
∴=.
∵AB=8,
∴AD=BD=4,
∴S阴影=S△ABC﹣S△ABD﹣S弓形AD
=S△ABC﹣S△ABD﹣(S扇形AOD﹣S△ABD)
=×8×8﹣×4×4﹣+××4×4
=16﹣4π+8
=24﹣4π.
故答案为:24﹣4π.
15.解:∵弦CD⊥AB于点E,
∴CE=cm,
∵OC=cm,
∴OE=cm,
∴∠OCE=30°,
∴∠COD=120°,
∴图中阴影部分面积=﹣×3×=π﹣cm2,
故答案为:π﹣cm2.
16.解:连接OD,
∵正方形的边长为1,即OC=CD=1,
∴OD=,
∴AC=OA﹣OC=﹣1,
∵DE=DC,BE=AC,弧BD=弧AD
∴S阴=长方形ACDF的面积=AC CD=﹣1.,
故答案为:﹣1
17.解:∵∠C=45°,
∴∠AOB=90°,
∴S阴影=S扇形AOB﹣S△AOB
=
=π﹣2.
故答案为:π﹣2.
18.解:∵AB⊥CD于E,∠COD=60°,
∴∠COB=30°,
∴图中阴影部分的面积=扇形OCB的面积=,
故答案为:3π.
19.解:该扇形的弧长==π,
该扇形的面积==,
故答案为:π,.
20.解:扇形的面积==18π,
故答案为:18π.
21.解:(1)如图,连接OB,
∵四边形OABC是一平行四边形,
∴AB=OC,
∵OA=OB=OC,
∴AB=OA=OB,即△OAB是等边三角形,
∴∠AOB=60°,同理∠BOC=60°,
∴∠AOC=120°;
(2)S阴影=扇形OAB的面积﹣三角形OAB的面积
=π×32﹣×32
=.
22.解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=6cm,AC=8cm,
∴由勾股定理得:AB=10cm,
∴OB=5cm,
连接OD,
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
∴BD===5cm;
(2)S阴影=S扇形ODB﹣S△ODB
=π 52﹣×5×5
=(cm2).
23.解:(1)∵AB是直径,
∴∠ACB=90°,
又∵BC=2,AB=4,
∴BC=AB,
∴∠BAC=30°,
∴∠DAB=∠DAC+∠BAC=15°+30°=45°;
(2)连接OD,
∵直径AB=4,
∴半径OD=OA=2,
∵OA=OD,∠DAB=45°,
∴∠ADO=∠DAB=45°,
∴∠AOD=90°,
∴阴影部分的面积S=S扇形AOD﹣S△AOD=﹣×2×2=π﹣2.
一.弧长的计算
1.如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )
A.2+ B.+ C.+ D.2+
2.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )
A.1个 B.2个 C.3个 D.4个
3.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .
4.已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则所得到的三条弧的长度之和为 cm(结果保留π).
5.如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则凸轮的周长等于 .
6.如图,在△ABC中,∠A=70°,BC=4,以BC的中点D为圆心,2为半径作弧,分别交边AB、AC于E、F,则的长为 .
7.如图,⊙O的半径为5cm,弦AC垂直平分半径OB,则弧ABC的长为 cm.
8.一顶简易的圆锥形帐篷,帐篷收起来时伞面的长度有4米,撑开后帐篷高2米,则帐篷撑好后的底面直径是 米.
二.扇形面积的计算
9.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.﹣ B.﹣2 C.π﹣ D.﹣
10.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA=OB=OC=2,则这朵三叶花的面积为( )
A.3π﹣3 B.3π﹣6 C.6π﹣3 D.6π﹣6
11.如图,在矩形ABCD中,AB=2,BC=2,以点B为圆心,AB为半径画弧,交AC于点E,交BC于点F,则图中阴影部分的面积为( )
A.π B.﹣π C.π﹣ D.π
12.如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )
A.π B.2π C.3π D.4π
13.一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是 cm2.
14.如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π) .
15.如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为cm,弦CD的长为3cm,则图中阴影部分面积是 .
16.如图,扇形AOB的圆心角为直角,边长为1的正方形OCDE的顶点C,E,D分别在OA,OB,上,过点A作AF⊥ED,交ED的延长线于点F,则图中阴影部分的面积等于 .
17.如图,在⊙O中,OA=2,∠C=45°,则图中阴影部分的面积为 .
18.如图,AB是半径为6的⊙O的直径,CD是弦,且AB⊥CD于E,若∠COD=60°,则图中阴影部分的面积是 .
19.已知扇形的圆心角为60°,半径为3,则该扇形的弧长为 ,面积为 .
20.已知扇形的圆心角为45°,半径长为12,则该扇形的面积为 .
21.如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.
(1)求∠AOC的度数;
(2)若⊙O的半径为3,求图中阴影部分的面积.
22.已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
23.已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
(1)求∠DAB的度数;
(2)求图中阴影部分的面积(结果保留π).
参考答案
一.弧长的计算
1.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长l==,
∴阴影部分周长的最小值为2+.
故选:D.
2.解:①优弧比劣弧长,不一定,在同圆或等圆中结论成立,故①错误.
②三点可以确定一个圆,错误,应该是过不在同一直线上的三个点确定一个圆.故②错误.
③长度相等的弧是等弧,错误,长度相等的弧不一定相等,等弧的长度相等,故③错误.
④经过圆内的一个定点可以作无数条弦,故④正确.
故选:C.
3.解:,解得r=.
故答案为:.
4.解:方法一:
先求出正六边形的每一个内角=,
所得到的三条弧的长度之和=3×=2πcm;
方法二:先求出正六边形的每一个外角为60°,
得正六边形的每一个内角120°,
每条弧的度数为120°,
三条弧可拼成一整圆,其三条弧的长度之和为2πcm.
故答案为:2π.
5.
解:∵△ABC为正三角形,
∴∠A=∠B=∠C=60°,AB=AC=BC=1,
∴====,
根据题意可知凸轮的周长为三个弧长的和,
即凸轮的周长=++=3×=π.
故答案为:π
6.解:由题意,DB=DE=DF=2,
∴∠B=∠DEB,∠C=∠DFC,
∵∠A=70°,
∴∠B+∠C=110°,
∴∠BDE+∠CDF=360°﹣2(∠B+∠C)=140°,
∴∠EDF=180°﹣140°=40°,
∴的长==π,
故答案为:π.
7.解:∵弦AC垂直平分半径OB,
∴AO=AB,CO=CB,
∴OA=AB=OB=OC=BC,
∴△OAB和△OBC都是等边三角形,
∴∠AOB=∠COB=60°,
∴∠AOC=120°,
∴弧ABC的长==π(cm).
故答案为π.
8.解:r===2,
直径为4米.
二.扇形面积的计算
9.解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:﹣×2×1=π﹣.
故选:A.
10.解:如图所示:弧OA是⊙M上满足条件的一段弧,连接AM、MO,
由题意知:∠AMO=90°,AM=OM
∵AO=2,∴AM=.
∵S扇形AMO=×π×MA2=.
S△AMO=AM MO=1,
∴S弓形AO=﹣1,
∴S三叶花=6×(﹣1)
=3π﹣6.
故选:B.
11.解:连接BE,过E作EH⊥BC于H,
在矩形ABCD中,∵∠ABC=90°,AB=2,BC=2,
∴tan∠BAC==,
∴∠BAC=60°,
∵BA=BE,
∴△ABE是等边三角形,
∴∠ABE=60°,
∴∠EBH=30°,
∴EH=BE=1,
∴S阴=S扇形BAE+S△BCE﹣S△ABE﹣S扇形BEF=+﹣﹣=,
故选:A.
12.解:根据三角形的外角和是360°以及扇形的面积公式,得阴影部分的面积和是:=4π.
故选:D.
13.解:设扇形的半径为Rcm,
∵扇形的圆心角为135°,弧长为3πcm,
∴=3π,
解得:R=4,
所以此扇形的面积为=6π(cm2),
故答案为:6π.
14.解:连接AD,OD,
∵等腰直角△ABC中,
∴∠ABD=45°.
∵AB是圆的直径,
∴∠ADB=90°,
∴△ABD也是等腰直角三角形,
∴=.
∵AB=8,
∴AD=BD=4,
∴S阴影=S△ABC﹣S△ABD﹣S弓形AD
=S△ABC﹣S△ABD﹣(S扇形AOD﹣S△ABD)
=×8×8﹣×4×4﹣+××4×4
=16﹣4π+8
=24﹣4π.
故答案为:24﹣4π.
15.解:∵弦CD⊥AB于点E,
∴CE=cm,
∵OC=cm,
∴OE=cm,
∴∠OCE=30°,
∴∠COD=120°,
∴图中阴影部分面积=﹣×3×=π﹣cm2,
故答案为:π﹣cm2.
16.解:连接OD,
∵正方形的边长为1,即OC=CD=1,
∴OD=,
∴AC=OA﹣OC=﹣1,
∵DE=DC,BE=AC,弧BD=弧AD
∴S阴=长方形ACDF的面积=AC CD=﹣1.,
故答案为:﹣1
17.解:∵∠C=45°,
∴∠AOB=90°,
∴S阴影=S扇形AOB﹣S△AOB
=
=π﹣2.
故答案为:π﹣2.
18.解:∵AB⊥CD于E,∠COD=60°,
∴∠COB=30°,
∴图中阴影部分的面积=扇形OCB的面积=,
故答案为:3π.
19.解:该扇形的弧长==π,
该扇形的面积==,
故答案为:π,.
20.解:扇形的面积==18π,
故答案为:18π.
21.解:(1)如图,连接OB,
∵四边形OABC是一平行四边形,
∴AB=OC,
∵OA=OB=OC,
∴AB=OA=OB,即△OAB是等边三角形,
∴∠AOB=60°,同理∠BOC=60°,
∴∠AOC=120°;
(2)S阴影=扇形OAB的面积﹣三角形OAB的面积
=π×32﹣×32
=.
22.解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=6cm,AC=8cm,
∴由勾股定理得:AB=10cm,
∴OB=5cm,
连接OD,
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
∴BD===5cm;
(2)S阴影=S扇形ODB﹣S△ODB
=π 52﹣×5×5
=(cm2).
23.解:(1)∵AB是直径,
∴∠ACB=90°,
又∵BC=2,AB=4,
∴BC=AB,
∴∠BAC=30°,
∴∠DAB=∠DAC+∠BAC=15°+30°=45°;
(2)连接OD,
∵直径AB=4,
∴半径OD=OA=2,
∵OA=OD,∠DAB=45°,
∴∠ADO=∠DAB=45°,
∴∠AOD=90°,
∴阴影部分的面积S=S扇形AOD﹣S△AOD=﹣×2×2=π﹣2.
