人教版2021-2022学年数学七年级下册7.1.1有序数对 同步课堂练习(word版含答案)
文档属性
| 名称 | 人教版2021-2022学年数学七年级下册7.1.1有序数对 同步课堂练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 411.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 22:03:49 | ||
图片预览



文档简介
2021-2022年初中数学七年级下册同步(人教版)
7.1.1有序数对-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,小亮从学校到家所走最短路线是( )
A.(2,2)→(2,1)→(2,0)→(0,0)
B.(2,2)→(2,1)→(1,1)→(0,1)
C.(2,2)→(2,3)→(0,3)→(0,1)
D.(2,2)→(2,0)→(0,0)→(0,1)
2.以下有序数对书写正确的是( ).
A. B.5,6 C. D.
3.共享单车提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车,如图,“”为小白同学的位置,“”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是( )
A. B. C. D.
4.如果一类有序数对满足方程,则下列数对不属于这类的是( ).
A. B. C. D.
5.如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(3,4)→(4,2)→(4,0)
D.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
6.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
二、填空题
7.如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)?(3,2)?(3,3)?(2,3)?(1,3)表示由A到B的一条路径,用同样的方式写出一条由A到B的路径:____________________.
8.若某个电影院用表示5排12号,则3排4号可以表示为____________.
9.如果有序数对表示某栋楼房中a层楼b号房,那么有序数对和分别代表的是__________,______________.
10.如图,李老师家在2街与2巷的十字路口附近,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示李老师从家到学校上班的一条路线.请你用同样的方式写出从家到学校的另外一种路线:____________________________________________________________.
11.我们规定向东和向北方向为正,如向东走4米,再向北走6米,记作,则向西走5米,再向北走3米记作_________;数对表示___________.
12.教室5排2号可用有序数对表示,则2排5号用数对可表示为__.
三、解答题
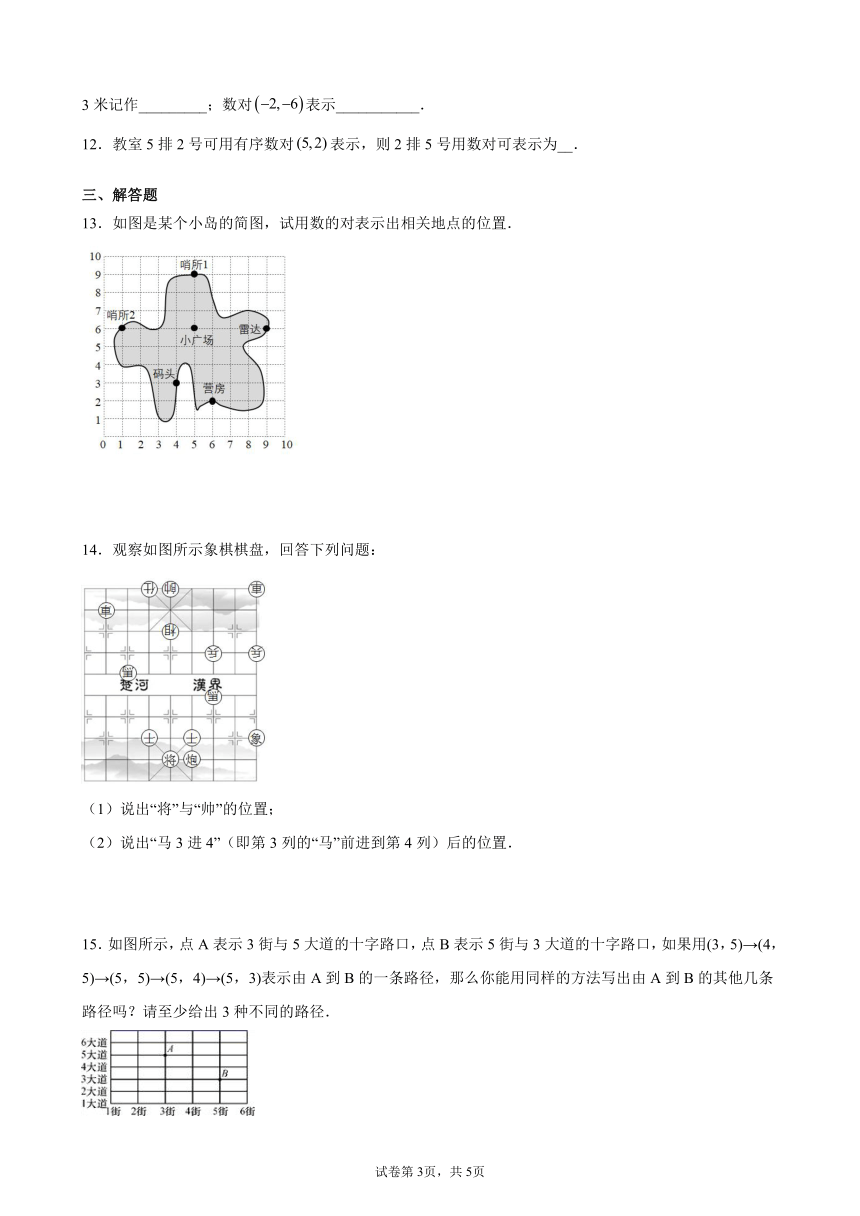
13.如图是某个小岛的简图,试用数的对表示出相关地点的位置.
14.观察如图所示象棋棋盘,回答下列问题:
(1)说出“将”与“帅”的位置;
(2)说出“马3进4”(即第3列的“马”前进到第4列)后的位置.
15.如图所示,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5)→(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?请至少给出3种不同的路径.
16.根据指令(s,A)(说明:s≥0,单位:厘米;0°≤A<180°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,若机器人站在点M处,面对的方向如图所示.
(1)给机器人下了一个指令(2,60°),机器人移动到了B点,请你画出机器人从M点到B点的运动路径;
(2)若机器人从M点运动到了C点,则给机器人下了一个什么指令?
17.如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息,那么图中
(1) A→C( , ),B→D( , ),C→ (+1, );
(2) 若甲虫A的爬行路线为A→B→C→D,请计算甲虫A爬行的路程;
(3) 若甲虫A的爬行路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),最终到达甲虫P处,请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置.
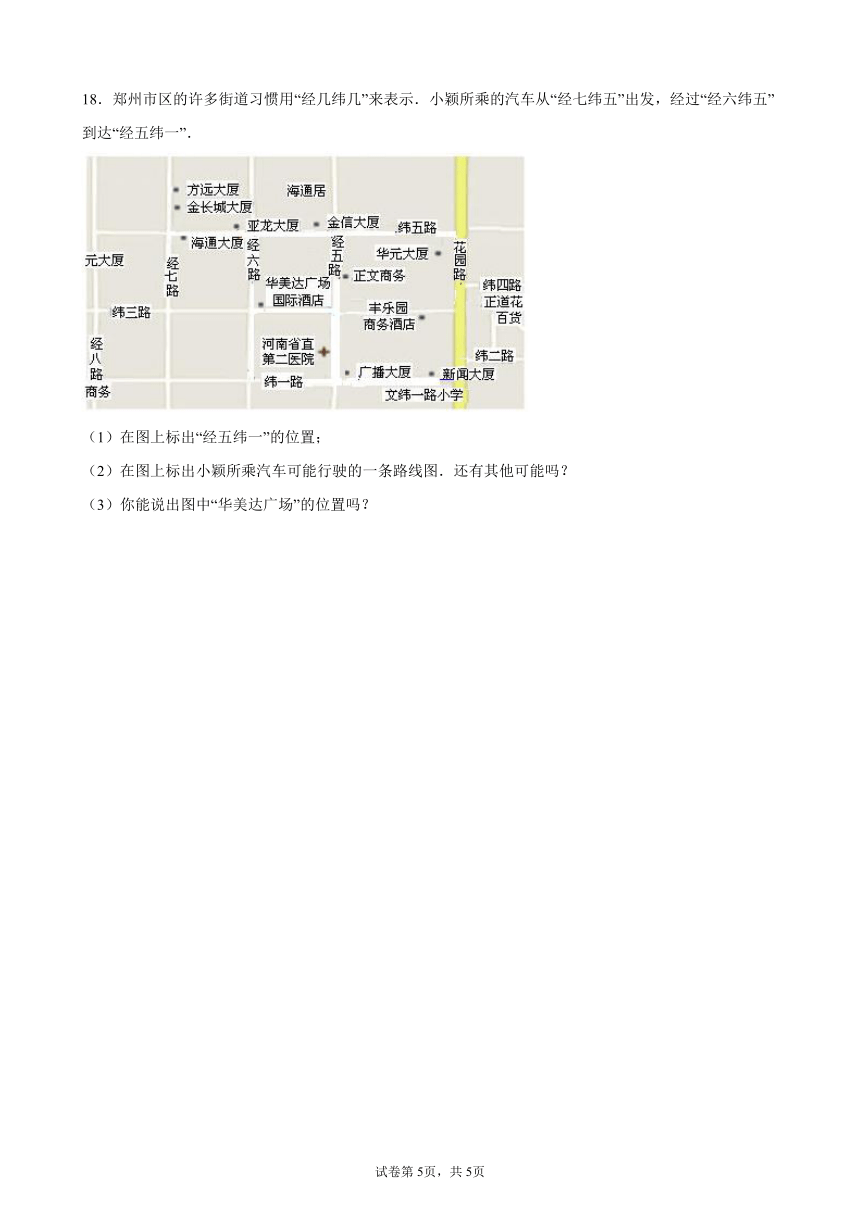
18.郑州市区的许多街道习惯用“经几纬几”来表示.小颖所乘的汽车从“经七纬五”出发,经过“经六纬五”到达“经五纬一”.
(1)在图上标出“经五纬一”的位置;
(2)在图上标出小颖所乘汽车可能行驶的一条路线图.还有其他可能吗?
(3)你能说出图中“华美达广场”的位置吗?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】由图可知小亮从学校到家所走最短路线是(2,2)→(2,1)→(1,1)→(0,1),故选B.
2.C
【解析】解:两个数之间使用的是顿号,故不符合题意;
5,6没有使用括号,故不符合题意;
是有序实数对的规范书写,故符合题意;
两个数之间没使用逗号,故不符合题意;
故选:
3.C
【解析】解:距E6最近的是F6,
故选:C.
4.C
【解析】解: 一类有序数对满足方程,
而
选项符合故不符合题意;
选项不符合故符合题意;
故选:
5.C
【解析】A、(0,4)→(0,0)→(4,0)都能到达,故本选项错误;
B、(0,4)→(4,4)→(4,0)都能到达,故本选项错误;
C、(3,4)→(4,2)不都能到达,故本选项正确;
D、(0,4)→(1,4)→(1,1)→(4,1)→(4,0)都能到达,故本选项错误.
故选C.
6.B
【解析】解: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:
7.(3,1)→(2,1)→(2,2)→(2,3)→(1,3)
【解析】横坐标表示经路,纵坐标表示纬路.然后结合图形画出路线,写出对应的坐标即可:一条由A到B的路径(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
故答案是:(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
8.
【解析】解:电影院里第5排12号可以表示为(5,12),那么3排4号可以表示为 (3,4).
故答案为:(3,4).
9.4层楼3号房; 3层楼4号房
【解析】解: 有序数对表示某栋楼房中a层楼b号房,
有序数对表示某栋楼房中4层楼3号房,
有序数对表示某栋楼房中3层楼4号房,
故答案为:4层楼3号房;3层楼4号房
10.答案不唯一:如(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4)
【解析】李老师从家到学校上班的路线可以沿走2巷走到5街,然后到学校,即(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
故答案为(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
11.; 向西走2米,再向南走6米
【解析】解:由题意得:向西走5米,再向北走3米记作:
数对表示向西走2米,再向南走6米,
故答案为:;向西走2米,再向南走6米.
12.
【解析】解:排2号可用有序数对表示,
排5号用数对可表示为.
13.码头,营房,雷达,小广场,哨所1,哨所2
【解析】根据题图可知,码头,营房,雷达,小广场,哨所1,哨所2
14.(1)“将”在第9行第5列,“帅”在第1行第5列;(2)第7行第4列
【解析】(1)按照图中的表示数字,“将”在第9行第5列,“帅”在第1行第5列;
(2)第7行第4列.
15.答案见解析.
【解析】答案不唯一,如:
(1)(3,5)→(4,5)→(4,4)→(5,4)→(5,3);
(2)(3,5)→(4,5)→(4,4)→(4,3)→(5,3);
(3)(3,5)→(3,4)→(4,4)→(5,4)→(5,3);
(4)(3,5)→(3,4)→(4,4)→(4,3)→(5,3);
(5)(3,5)→(3,4)→(3,3)→(4,3)→(5,3)等.
16.(1)画图略
(2)指令(3,20°)
【解析】(1)如图:
(2)给机器人的指令是(3,20°).
17.(1)A→C(+3 ,+4 ),B→D(+3 ,-2 ),C→ D (+1,-2 );(2) 10;(3)见解析.
【解析】解:(1)A→C(+3,+4);B→D(+3,﹣2);C→D(+1,﹣2);
(2)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);则该甲虫走过的路线长为1+4+2+0+1+2=10.
答:甲虫A爬行的路程为10;
(3)甲虫A爬行示意图与点P的位置如图所示:
18.(1)“经五纬一”在广播大厦旁边的十字路口;(2)“经七纬五”“经六纬五”“经五纬五”“经五纬五”到达“经五纬一”;(3)“华美达广场”位于“经六路”与“纬三路”的十字路口附近
【解析】解:(1)如图:“经五纬一”在广播大厦旁边的十字路口.
(2)如图:从“经七纬五”到达“经五纬一”的路线不唯一.例如,“经七纬五”“经六纬五”“经五纬五”“经五纬五”到达“经五纬一”.
(3)“华美达广场”位于“经六路”与“纬三路”的十字路口附近.
答案第1页,共2页
答案第1页,共2页
7.1.1有序数对-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,小亮从学校到家所走最短路线是( )
A.(2,2)→(2,1)→(2,0)→(0,0)
B.(2,2)→(2,1)→(1,1)→(0,1)
C.(2,2)→(2,3)→(0,3)→(0,1)
D.(2,2)→(2,0)→(0,0)→(0,1)
2.以下有序数对书写正确的是( ).
A. B.5,6 C. D.
3.共享单车提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车,如图,“”为小白同学的位置,“”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是( )
A. B. C. D.
4.如果一类有序数对满足方程,则下列数对不属于这类的是( ).
A. B. C. D.
5.如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(3,4)→(4,2)→(4,0)
D.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
6.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
二、填空题
7.如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)?(3,2)?(3,3)?(2,3)?(1,3)表示由A到B的一条路径,用同样的方式写出一条由A到B的路径:____________________.
8.若某个电影院用表示5排12号,则3排4号可以表示为____________.
9.如果有序数对表示某栋楼房中a层楼b号房,那么有序数对和分别代表的是__________,______________.
10.如图,李老师家在2街与2巷的十字路口附近,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示李老师从家到学校上班的一条路线.请你用同样的方式写出从家到学校的另外一种路线:____________________________________________________________.
11.我们规定向东和向北方向为正,如向东走4米,再向北走6米,记作,则向西走5米,再向北走3米记作_________;数对表示___________.
12.教室5排2号可用有序数对表示,则2排5号用数对可表示为__.
三、解答题
13.如图是某个小岛的简图,试用数的对表示出相关地点的位置.
14.观察如图所示象棋棋盘,回答下列问题:
(1)说出“将”与“帅”的位置;
(2)说出“马3进4”(即第3列的“马”前进到第4列)后的位置.
15.如图所示,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5)→(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?请至少给出3种不同的路径.
16.根据指令(s,A)(说明:s≥0,单位:厘米;0°≤A<180°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,若机器人站在点M处,面对的方向如图所示.
(1)给机器人下了一个指令(2,60°),机器人移动到了B点,请你画出机器人从M点到B点的运动路径;
(2)若机器人从M点运动到了C点,则给机器人下了一个什么指令?
17.如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息,那么图中
(1) A→C( , ),B→D( , ),C→ (+1, );
(2) 若甲虫A的爬行路线为A→B→C→D,请计算甲虫A爬行的路程;
(3) 若甲虫A的爬行路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),最终到达甲虫P处,请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置.
18.郑州市区的许多街道习惯用“经几纬几”来表示.小颖所乘的汽车从“经七纬五”出发,经过“经六纬五”到达“经五纬一”.
(1)在图上标出“经五纬一”的位置;
(2)在图上标出小颖所乘汽车可能行驶的一条路线图.还有其他可能吗?
(3)你能说出图中“华美达广场”的位置吗?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】由图可知小亮从学校到家所走最短路线是(2,2)→(2,1)→(1,1)→(0,1),故选B.
2.C
【解析】解:两个数之间使用的是顿号,故不符合题意;
5,6没有使用括号,故不符合题意;
是有序实数对的规范书写,故符合题意;
两个数之间没使用逗号,故不符合题意;
故选:
3.C
【解析】解:距E6最近的是F6,
故选:C.
4.C
【解析】解: 一类有序数对满足方程,
而
选项符合故不符合题意;
选项不符合故符合题意;
故选:
5.C
【解析】A、(0,4)→(0,0)→(4,0)都能到达,故本选项错误;
B、(0,4)→(4,4)→(4,0)都能到达,故本选项错误;
C、(3,4)→(4,2)不都能到达,故本选项正确;
D、(0,4)→(1,4)→(1,1)→(4,1)→(4,0)都能到达,故本选项错误.
故选C.
6.B
【解析】解: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:
7.(3,1)→(2,1)→(2,2)→(2,3)→(1,3)
【解析】横坐标表示经路,纵坐标表示纬路.然后结合图形画出路线,写出对应的坐标即可:一条由A到B的路径(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
故答案是:(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
8.
【解析】解:电影院里第5排12号可以表示为(5,12),那么3排4号可以表示为 (3,4).
故答案为:(3,4).
9.4层楼3号房; 3层楼4号房
【解析】解: 有序数对表示某栋楼房中a层楼b号房,
有序数对表示某栋楼房中4层楼3号房,
有序数对表示某栋楼房中3层楼4号房,
故答案为:4层楼3号房;3层楼4号房
10.答案不唯一:如(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4)
【解析】李老师从家到学校上班的路线可以沿走2巷走到5街,然后到学校,即(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
故答案为(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
11.; 向西走2米,再向南走6米
【解析】解:由题意得:向西走5米,再向北走3米记作:
数对表示向西走2米,再向南走6米,
故答案为:;向西走2米,再向南走6米.
12.
【解析】解:排2号可用有序数对表示,
排5号用数对可表示为.
13.码头,营房,雷达,小广场,哨所1,哨所2
【解析】根据题图可知,码头,营房,雷达,小广场,哨所1,哨所2
14.(1)“将”在第9行第5列,“帅”在第1行第5列;(2)第7行第4列
【解析】(1)按照图中的表示数字,“将”在第9行第5列,“帅”在第1行第5列;
(2)第7行第4列.
15.答案见解析.
【解析】答案不唯一,如:
(1)(3,5)→(4,5)→(4,4)→(5,4)→(5,3);
(2)(3,5)→(4,5)→(4,4)→(4,3)→(5,3);
(3)(3,5)→(3,4)→(4,4)→(5,4)→(5,3);
(4)(3,5)→(3,4)→(4,4)→(4,3)→(5,3);
(5)(3,5)→(3,4)→(3,3)→(4,3)→(5,3)等.
16.(1)画图略
(2)指令(3,20°)
【解析】(1)如图:
(2)给机器人的指令是(3,20°).
17.(1)A→C(+3 ,+4 ),B→D(+3 ,-2 ),C→ D (+1,-2 );(2) 10;(3)见解析.
【解析】解:(1)A→C(+3,+4);B→D(+3,﹣2);C→D(+1,﹣2);
(2)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);则该甲虫走过的路线长为1+4+2+0+1+2=10.
答:甲虫A爬行的路程为10;
(3)甲虫A爬行示意图与点P的位置如图所示:
18.(1)“经五纬一”在广播大厦旁边的十字路口;(2)“经七纬五”“经六纬五”“经五纬五”“经五纬五”到达“经五纬一”;(3)“华美达广场”位于“经六路”与“纬三路”的十字路口附近
【解析】解:(1)如图:“经五纬一”在广播大厦旁边的十字路口.
(2)如图:从“经七纬五”到达“经五纬一”的路线不唯一.例如,“经七纬五”“经六纬五”“经五纬五”“经五纬五”到达“经五纬一”.
(3)“华美达广场”位于“经六路”与“纬三路”的十字路口附近.
答案第1页,共2页
答案第1页,共2页
