2021--2022学年人教版八年级数学下册20.2数据的波动程度同步练习(word解析版)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册20.2数据的波动程度同步练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 57.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 22:24:57 | ||
图片预览




文档简介
八年级下册第二十章20.2数据的波动程度
一、选择题
已知一组数据的方差是,则这组数据的标准差是
A. B. C. D.
一组数据,,,,的标准差是
A. B. C. D.
小甬参加射击比赛,成绩统计如表:
成绩环
次数
关于他的射击成绩,下列说法正确的是
A. 平均数是环 B. 标准差为环 C. 众数是环 D. 中位数是环
某小组五位同学参加某次考试满分分的平均成绩是分,其中三位男生成绩的方差为,两位女生的成绩分别为分、分,则这五位同学成绩的标准差为
A. B. C. D.
一组数据,,,的平均数为,方差为,其中是正整数,则另一组数据,,,的平均数和标准差分别是
A. , B. , C. , D. ,
已知一组数据:,,,,,,,则这组数据的极差是
A. B. C. D.
一组数据,,,,,它们的数据分析正确的是
A. 平均数是 B. 中位数是 C. 方差是 D. 极差是
为了大力宣传节约用电,某小区随机抽查了户家庭的月用电量情况,统计如下表,关于这户家庭的月用电量说法正确的是
月用电量度
户数
A. 极差是 B. 众数是 C. 中位数 D. 平均数是
已知一组数据,,,,,以下说法错误的是
A. 平均数是 B. 众数是 C. 中位数是 D. 方差是
在轮“中国汉字听写大赛”选拔赛中,甲、乙两位同学的平均分都是分,甲的成绩方差是,乙的成绩方差是,下列说法正确的是
A. 甲的成绩比乙的成绩稳定 B. 乙的成绩比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定 D. 无法确定甲、乙的成绩谁更稳定
已知一组数据为,,,,,,,用计算器计算这组数据的方差精确到为
A. B. C. D.
已知一组数据,,的平均数为,方差为,那么数据,,的平均数和方差分别是
A. , B. , C. , D. ,
二、填空题
用计算器的统计功能求标准差,要先进入统计计算状态,按______键即可进入统计计算状态.
一组数据、、、、、的方差是 .
一组数据,,,,,的极差是____.
从甲、乙两种玉米种子中选择一种合适的推荐给某地.考虑到庄稼人对玉米的产量和产量的稳定性十分的关心.选择之前,为了解甲、乙两种玉米种子的情况,某单位各用了块自然条件相同的试验田进行试验,得到各试验田每公顷产量单位:的数据,这两组数据的平均数分别是约等于,约等于,方差分别是,,你认为应该选择的玉米种子是______.
三、解答题
某校八年级班甲、乙两男生在次引体向上测试中有效次数如下:
甲:,,,,;乙:,,,,;
甲乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数 众数 中位数 方差
甲
乙
根据以上信息,回答下列问题:
表格是______,______,______填数值
体育老师根据这次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是______班主任李老师根据去年比赛的成绩至少次才能获奖,决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是______.
如果乙同学再做一次引体向上,有效次数为,那么乙同学次引体向上成绩的平均数______,中位数______,方差______填“变大”、“变小”或“不变”
某校要从甲、乙两个跳远运动员中选一人参加一项比赛,在最近的次选拨赛中,他们的成绩单位:如下:
甲:,,,,,,,,,
乙:,,,,,,,,,
分别求甲、乙的平均成绩;
分别求甲、乙这十次成绩的方差;
这两名运动员的运动成绩各有什么特点?历届比赛成绩表明,成绩达到就很可能夺冠你认为应选谁参加比赛?
省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩单位:环如下表:
第一次 第二次 第三次 第四次 第五次 第六次
甲
乙
根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环
分别计算甲、乙六次测试成绩的方差
根据的计算结果,你认为推荐谁参加全国比赛更合适请说明理由计算方差的公式:
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取株,并测得它们的株高单位:如下表所示:
甲
乙
请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐.
甲、乙两位同学次数学选拔赛的成绩统计如表,他们次考试的总成绩相同,请完成下列问题:
第次 第次 第次 第次 第次
甲
乙
统计表中, ,甲同学成绩的极差为
小颖计算了甲同学成绩的平均数为,方差,请你求出乙同学成绩的平均数和方差
从平均数和方差的角度分析,甲、乙两位同学谁的成绩更稳定.
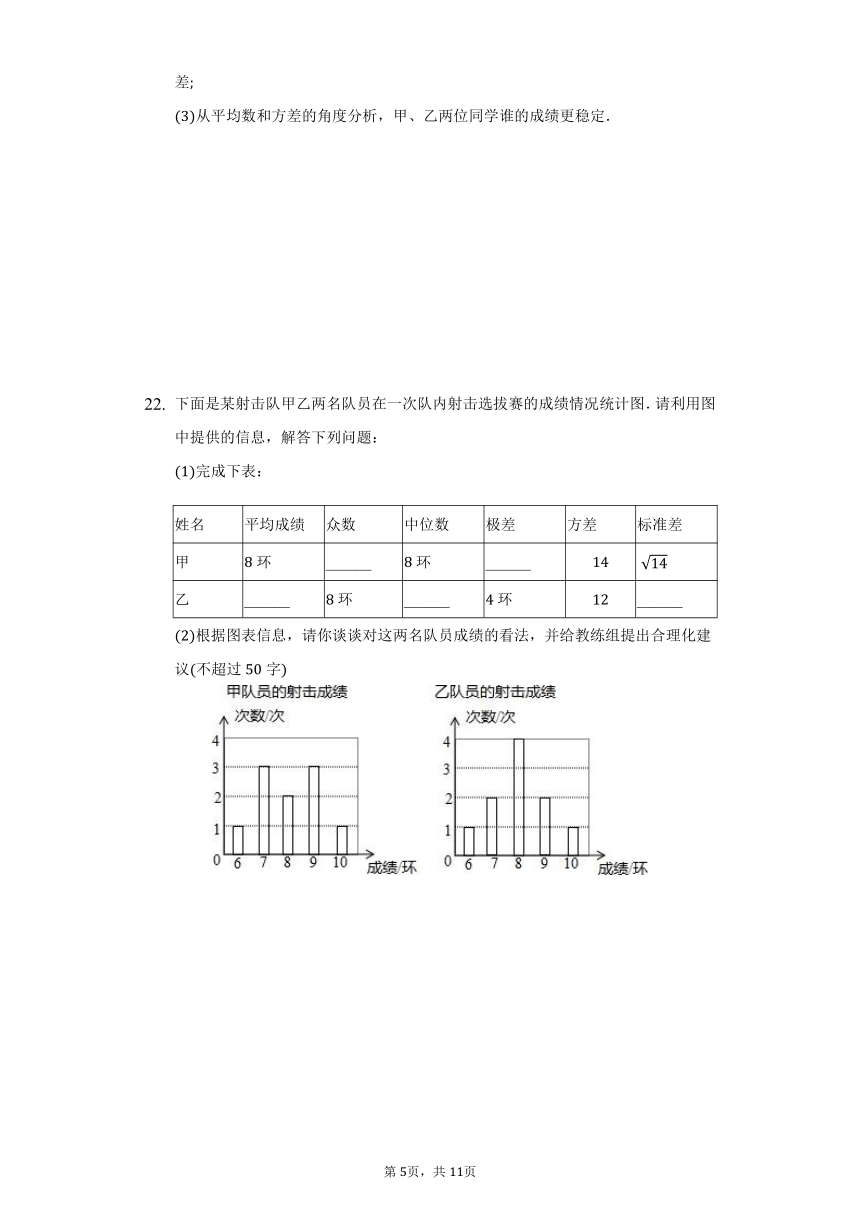
下面是某射击队甲乙两名队员在一次队内射击选拔赛的成绩情况统计图.请利用图中提供的信息,解答下列问题:
完成下表:
姓名 平均成绩 众数 中位数 极差 方差 标准差
甲 环 ______ 环 ______
乙 ______ 环 ______ 环 ______
根据图表信息,请你谈谈对这两名队员成绩的看法,并给教练组提出合理化建议不超过字
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】解:数据的平均数,
方差
,
故五个数据的标准差是.
故选A.
3.【答案】
【解析】解:这组数据的平均数为环,此选项错误;
B.方差为,
则标准差为环,此选项错误;
C.众数为环和环,此选项错误;
D.中位数是环,此选项正确;
故选:.
4.【答案】
【解析】解:三位男生的方差,
,
这个学习小组位同学考试分数的方差
,
标准差是,
故选:.
5.【答案】
【解析】解:,,,的平均数是,则.
,
.
标准差为.
故选:.
6.【答案】
【解析】解:由题意可知,极差为.
故选A.
根据极差的定义用一组数据中的最大值减去最小值即可求得.
本题考查了极差的定义,求极差的方法是用一组数据中的最大值减去最小值.
7.【答案】
【解析】解:将数据重新排列为、、、、,
则这组数据的平均数为,中位数为,
方差为,
极差为,
故选:.
8.【答案】
【解析】解:、这组数据的极差是:,故本选项错误;
B、出现的次数最多,出现了次,则众数是,故本选项错误;
C、把这些数从小到大排列,最中间两个数的平均数是,则中位数是,故本选项正确;
D、这组数据的平均数,故本选项错误;
故选C.
9.【答案】
【解析】解:由平均数的公式得平均数,
方差,
将个数按从小到大的顺序排列为:,,,,,第个数为,即中位数为,
个数中出现了两次,次数最多,即众数为,
故选:.
10.【答案】
【解析】解:乙的成绩方差甲成绩的方差,
乙的成绩比甲的成绩稳定,
故选:.
11.【答案】
【解析】第一步:开机;
第二步:按,再按,出现;
第三步:按,再按,出现,再按;
第四步:输入数据,输完每个都按,出现输入数据个数;
第五步,按,再按,按,,,,显示出方差,
精确到为.
注意不同的计算器操作程序可能不同
故选C.
12.【答案】
【解析】解:数据,,的平均数为,
,
,
数据,,的平均数是;
数据,,的方差为,
,
,,的方差--.
故选:.
13.【答案】
【解析】解:用计算器求方差的一般步骤是:
使计算器进入 状态;
依次输入各数据;
按求的功能键,即可得出结果.
故答案为: .
由于不同的计算器,其操作不完全相同,可以根据计算器的说明书进行操作.
此题主要考查了计算器求方差,正确掌握计算器的基本使用方法是解题关键.
14.【答案】
【解析】略
15.【答案】
【解析】解:数据,,,,,的极差是.
故答案为:.
16.【答案】乙
【解析】解:,,,
,
乙玉米种子的产量比较稳定,
应该选择的玉米种子是乙,
故答案为:乙.
17.【答案】 甲的方差较小,比较稳定 乙的中位数是,众数是,获奖次数较多 不变 变小 变小
【解析】解:甲的成绩中,出现的次数最多,因此甲的众数是,即,
即,
将乙的成绩从小到大排列为,,,,,处在第位的数是,因此中位数是,即,
故答案为:,,.
甲的方差较小,比较稳定,乙的中位数是,众数是,获奖次数较多,
原平均数是,增加一次是,因此次的平均数还是,不变,
六次成绩排序为,,,,,,中位数是,比原来变小,方差变小,
故答案为:不变,变小,变小.
根据中位数、众数、平均数的计算方法分别计算结果,得出答案,
选择甲,只要看甲的方差较小,发挥稳定,选择乙由于乙的众数较大,中位数较大,成绩在中位数以上的占一半,获奖的次数较多,
加入一次成绩为之后,计算个数的平均数、众数、中位数,做出判断.
考查平均数、中位数、众数的意义和计算方法,明确各个统计量的意义,反映数据的特征以及计算方法是正确解答的关键.
18.【答案】解:,;
,
.
由且知,甲平均成绩高且比乙的成绩稳定,
甲次成绩中有次成绩达到,而乙次成绩中只有次达到,而且甲的成绩稳定,
应该选择甲参加比赛.
19.【答案】解:;;
;
;
推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
20.【答案】解:.
.
.
.
.
乙种小麦长势整齐.
【解析】先计算出平均数,再依据方差公式即可得.
本题考查方差的定义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
21.【答案】解:.
乙同学成绩的平均数,
方差.
因为甲、乙两位同学成绩的平均数相同,,所以乙同学的成绩更稳定.
22.【答案】环与环;环;环;环;
对于甲与乙这两名队员的成绩,他们的平均数、中位数与极差都相同,但是乙的方差较小,故乙的成绩更加稳定.
【解析】解:甲的成绩中,环与环都出现了次,次数最多,故众数为环与环;
极差是:环;
乙的平均成绩环,
乙第成绩为环,第成绩环,中位数为环,
标准差为.
填表如下:
姓名 平均成绩 众数 中位数 极差 方差 标准差
甲 环 环与环 环 环
乙 环 环 环 环
对于甲与乙这两名队员的成绩,他们的平均数、中位数与极差都相同,但是乙的方差较小,故乙的成绩更加稳定.
根据平均数、众数、中位数、方差的计算方法计算即可.
根据实际情况,给出合理的建议.
本题考查的是平均数、众数、中位数和方差的概念.要学会从统计图中得出正确的结论.
第2页,共2页
第1页,共1页
一、选择题
已知一组数据的方差是,则这组数据的标准差是
A. B. C. D.
一组数据,,,,的标准差是
A. B. C. D.
小甬参加射击比赛,成绩统计如表:
成绩环
次数
关于他的射击成绩,下列说法正确的是
A. 平均数是环 B. 标准差为环 C. 众数是环 D. 中位数是环
某小组五位同学参加某次考试满分分的平均成绩是分,其中三位男生成绩的方差为,两位女生的成绩分别为分、分,则这五位同学成绩的标准差为
A. B. C. D.
一组数据,,,的平均数为,方差为,其中是正整数,则另一组数据,,,的平均数和标准差分别是
A. , B. , C. , D. ,
已知一组数据:,,,,,,,则这组数据的极差是
A. B. C. D.
一组数据,,,,,它们的数据分析正确的是
A. 平均数是 B. 中位数是 C. 方差是 D. 极差是
为了大力宣传节约用电,某小区随机抽查了户家庭的月用电量情况,统计如下表,关于这户家庭的月用电量说法正确的是
月用电量度
户数
A. 极差是 B. 众数是 C. 中位数 D. 平均数是
已知一组数据,,,,,以下说法错误的是
A. 平均数是 B. 众数是 C. 中位数是 D. 方差是
在轮“中国汉字听写大赛”选拔赛中,甲、乙两位同学的平均分都是分,甲的成绩方差是,乙的成绩方差是,下列说法正确的是
A. 甲的成绩比乙的成绩稳定 B. 乙的成绩比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定 D. 无法确定甲、乙的成绩谁更稳定
已知一组数据为,,,,,,,用计算器计算这组数据的方差精确到为
A. B. C. D.
已知一组数据,,的平均数为,方差为,那么数据,,的平均数和方差分别是
A. , B. , C. , D. ,
二、填空题
用计算器的统计功能求标准差,要先进入统计计算状态,按______键即可进入统计计算状态.
一组数据、、、、、的方差是 .
一组数据,,,,,的极差是____.
从甲、乙两种玉米种子中选择一种合适的推荐给某地.考虑到庄稼人对玉米的产量和产量的稳定性十分的关心.选择之前,为了解甲、乙两种玉米种子的情况,某单位各用了块自然条件相同的试验田进行试验,得到各试验田每公顷产量单位:的数据,这两组数据的平均数分别是约等于,约等于,方差分别是,,你认为应该选择的玉米种子是______.
三、解答题
某校八年级班甲、乙两男生在次引体向上测试中有效次数如下:
甲:,,,,;乙:,,,,;
甲乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数 众数 中位数 方差
甲
乙
根据以上信息,回答下列问题:
表格是______,______,______填数值
体育老师根据这次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是______班主任李老师根据去年比赛的成绩至少次才能获奖,决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是______.
如果乙同学再做一次引体向上,有效次数为,那么乙同学次引体向上成绩的平均数______,中位数______,方差______填“变大”、“变小”或“不变”
某校要从甲、乙两个跳远运动员中选一人参加一项比赛,在最近的次选拨赛中,他们的成绩单位:如下:
甲:,,,,,,,,,
乙:,,,,,,,,,
分别求甲、乙的平均成绩;
分别求甲、乙这十次成绩的方差;
这两名运动员的运动成绩各有什么特点?历届比赛成绩表明,成绩达到就很可能夺冠你认为应选谁参加比赛?
省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩单位:环如下表:
第一次 第二次 第三次 第四次 第五次 第六次
甲
乙
根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环
分别计算甲、乙六次测试成绩的方差
根据的计算结果,你认为推荐谁参加全国比赛更合适请说明理由计算方差的公式:
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取株,并测得它们的株高单位:如下表所示:
甲
乙
请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐.
甲、乙两位同学次数学选拔赛的成绩统计如表,他们次考试的总成绩相同,请完成下列问题:
第次 第次 第次 第次 第次
甲
乙
统计表中, ,甲同学成绩的极差为
小颖计算了甲同学成绩的平均数为,方差,请你求出乙同学成绩的平均数和方差
从平均数和方差的角度分析,甲、乙两位同学谁的成绩更稳定.
下面是某射击队甲乙两名队员在一次队内射击选拔赛的成绩情况统计图.请利用图中提供的信息,解答下列问题:
完成下表:
姓名 平均成绩 众数 中位数 极差 方差 标准差
甲 环 ______ 环 ______
乙 ______ 环 ______ 环 ______
根据图表信息,请你谈谈对这两名队员成绩的看法,并给教练组提出合理化建议不超过字
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】解:数据的平均数,
方差
,
故五个数据的标准差是.
故选A.
3.【答案】
【解析】解:这组数据的平均数为环,此选项错误;
B.方差为,
则标准差为环,此选项错误;
C.众数为环和环,此选项错误;
D.中位数是环,此选项正确;
故选:.
4.【答案】
【解析】解:三位男生的方差,
,
这个学习小组位同学考试分数的方差
,
标准差是,
故选:.
5.【答案】
【解析】解:,,,的平均数是,则.
,
.
标准差为.
故选:.
6.【答案】
【解析】解:由题意可知,极差为.
故选A.
根据极差的定义用一组数据中的最大值减去最小值即可求得.
本题考查了极差的定义,求极差的方法是用一组数据中的最大值减去最小值.
7.【答案】
【解析】解:将数据重新排列为、、、、,
则这组数据的平均数为,中位数为,
方差为,
极差为,
故选:.
8.【答案】
【解析】解:、这组数据的极差是:,故本选项错误;
B、出现的次数最多,出现了次,则众数是,故本选项错误;
C、把这些数从小到大排列,最中间两个数的平均数是,则中位数是,故本选项正确;
D、这组数据的平均数,故本选项错误;
故选C.
9.【答案】
【解析】解:由平均数的公式得平均数,
方差,
将个数按从小到大的顺序排列为:,,,,,第个数为,即中位数为,
个数中出现了两次,次数最多,即众数为,
故选:.
10.【答案】
【解析】解:乙的成绩方差甲成绩的方差,
乙的成绩比甲的成绩稳定,
故选:.
11.【答案】
【解析】第一步:开机;
第二步:按,再按,出现;
第三步:按,再按,出现,再按;
第四步:输入数据,输完每个都按,出现输入数据个数;
第五步,按,再按,按,,,,显示出方差,
精确到为.
注意不同的计算器操作程序可能不同
故选C.
12.【答案】
【解析】解:数据,,的平均数为,
,
,
数据,,的平均数是;
数据,,的方差为,
,
,,的方差--.
故选:.
13.【答案】
【解析】解:用计算器求方差的一般步骤是:
使计算器进入 状态;
依次输入各数据;
按求的功能键,即可得出结果.
故答案为: .
由于不同的计算器,其操作不完全相同,可以根据计算器的说明书进行操作.
此题主要考查了计算器求方差,正确掌握计算器的基本使用方法是解题关键.
14.【答案】
【解析】略
15.【答案】
【解析】解:数据,,,,,的极差是.
故答案为:.
16.【答案】乙
【解析】解:,,,
,
乙玉米种子的产量比较稳定,
应该选择的玉米种子是乙,
故答案为:乙.
17.【答案】 甲的方差较小,比较稳定 乙的中位数是,众数是,获奖次数较多 不变 变小 变小
【解析】解:甲的成绩中,出现的次数最多,因此甲的众数是,即,
即,
将乙的成绩从小到大排列为,,,,,处在第位的数是,因此中位数是,即,
故答案为:,,.
甲的方差较小,比较稳定,乙的中位数是,众数是,获奖次数较多,
原平均数是,增加一次是,因此次的平均数还是,不变,
六次成绩排序为,,,,,,中位数是,比原来变小,方差变小,
故答案为:不变,变小,变小.
根据中位数、众数、平均数的计算方法分别计算结果,得出答案,
选择甲,只要看甲的方差较小,发挥稳定,选择乙由于乙的众数较大,中位数较大,成绩在中位数以上的占一半,获奖的次数较多,
加入一次成绩为之后,计算个数的平均数、众数、中位数,做出判断.
考查平均数、中位数、众数的意义和计算方法,明确各个统计量的意义,反映数据的特征以及计算方法是正确解答的关键.
18.【答案】解:,;
,
.
由且知,甲平均成绩高且比乙的成绩稳定,
甲次成绩中有次成绩达到,而乙次成绩中只有次达到,而且甲的成绩稳定,
应该选择甲参加比赛.
19.【答案】解:;;
;
;
推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
20.【答案】解:.
.
.
.
.
乙种小麦长势整齐.
【解析】先计算出平均数,再依据方差公式即可得.
本题考查方差的定义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
21.【答案】解:.
乙同学成绩的平均数,
方差.
因为甲、乙两位同学成绩的平均数相同,,所以乙同学的成绩更稳定.
22.【答案】环与环;环;环;环;
对于甲与乙这两名队员的成绩,他们的平均数、中位数与极差都相同,但是乙的方差较小,故乙的成绩更加稳定.
【解析】解:甲的成绩中,环与环都出现了次,次数最多,故众数为环与环;
极差是:环;
乙的平均成绩环,
乙第成绩为环,第成绩环,中位数为环,
标准差为.
填表如下:
姓名 平均成绩 众数 中位数 极差 方差 标准差
甲 环 环与环 环 环
乙 环 环 环 环
对于甲与乙这两名队员的成绩,他们的平均数、中位数与极差都相同,但是乙的方差较小,故乙的成绩更加稳定.
根据平均数、众数、中位数、方差的计算方法计算即可.
根据实际情况,给出合理的建议.
本题考查的是平均数、众数、中位数和方差的概念.要学会从统计图中得出正确的结论.
第2页,共2页
第1页,共1页
