2022年河南省人教版中考数学总复习九年级下册4.7相似三角形学案
文档属性
| 名称 | 2022年河南省人教版中考数学总复习九年级下册4.7相似三角形学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-30 08:34:28 | ||
图片预览


文档简介
2022年河南省中考数学总复习
寒假阶段考点解析
第四章 三角形
第7节 相似三角形
【预学习内容课本范围】人教:九下P23~P46
【预学习目标定位导航】
1 了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割;
2 掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;
3 了解相似三角形的性质定理和判定定理;
4 通过具体实例认识图形的相似,了解相似多边形和相似比;
5 会利用图形的相似解决一些简单的实际问题;
6 了解相似三角形判定定理的证明;
7 了解图形的位似,知道利用位似可以将一个图形放大或缩小;
8 在直角坐标系中,探索并了解将一个多边形的顶点坐标(有一个顶点为原点、有一条边在横坐标轴上)分别扩大或缩小相同倍数时所对应的图形与原图形是位似的.
【预学习考点解读分析】
考点1.比例及其性质
1.定义:两个比相等的式子叫做比例,比如=.
2.基本性质:= .(a,b,c,d都不等于0)
3.合比性质:= =② .(bd≠0)
4.等比性质:==…=(b+d+…+n≠0) =③ .
5.平行线分线段成比例
定理:两条直线被一组平行线所截,所得的对应线段成比例.
如图,由l1∥l2∥l3,可得:
(1)=;(2)=④ ;(3)= .
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
【特别提示】求两条线段的比时,要统一长度单位.
考点2.黄金分割:把一条线段分成两条线段,使较长的线段是原线段与较短的线段的比例中项,叫做把这条线段黄金分割.如图,在线段AB上,点C把线段AB分成两条线段AC和BC(AC>BC),如果=,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,且黄金比为=≈0.618.
【特别提示】一条线段的黄金分割点有2个.
考点3.相似三角形的判定与性质:
1.相似的概念:(1)定义:三个角分别相等,三条边成比例的两个三角形叫做相似三角形.(2)相似比:相似三角形对应边的比叫做相似比(或叫做相似系数).特别地,当相似比等于1时,两个三角形全等.
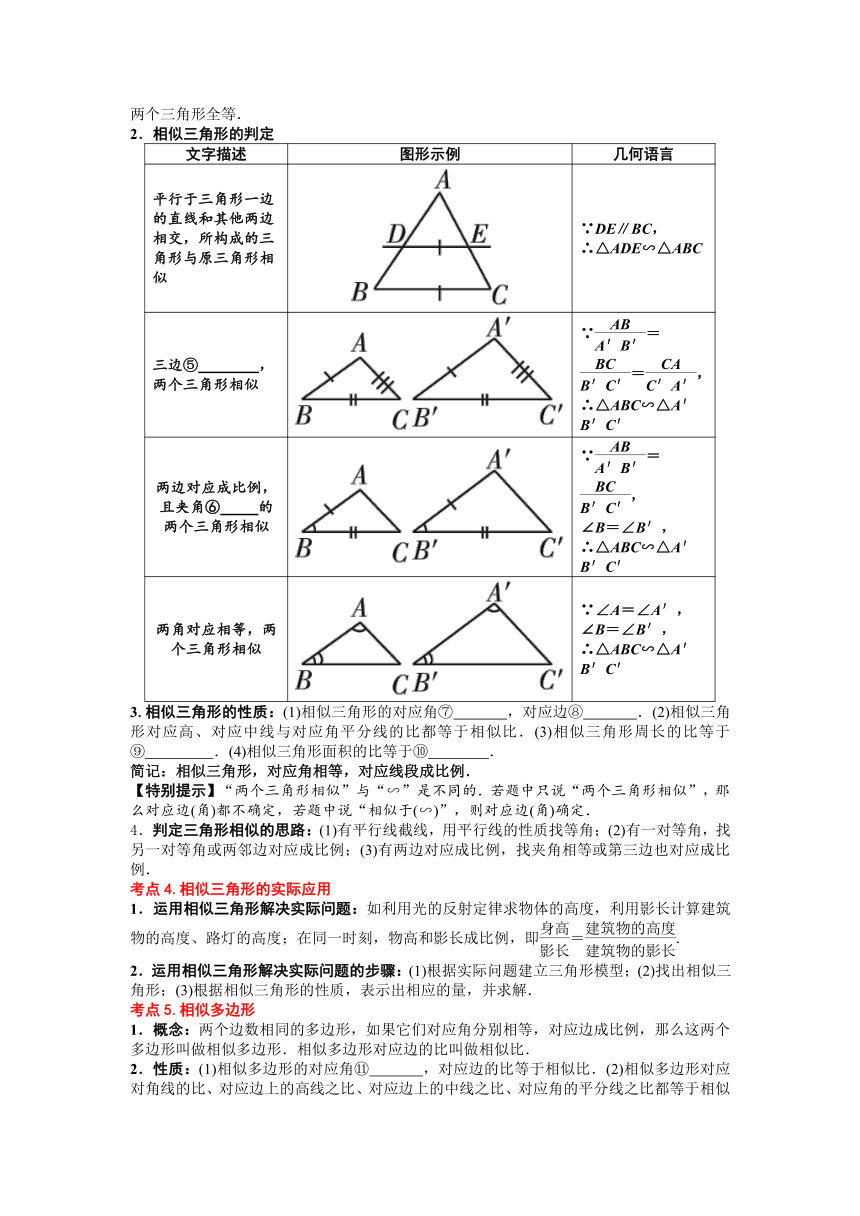
2.相似三角形的判定
文字描述 图形示例 几何语言
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似 ∵DE∥BC, ∴△ADE∽△ABC
三边⑤ ,两个三角形相似 ∵==, ∴△ABC∽△A′B′C′
两边对应成比例,且夹角⑥ 的两个三角形相似 ∵=, ∠B=∠B′, ∴△ABC∽△A′B′C′
两角对应相等,两个三角形相似 ∵∠A=∠A′, ∠B=∠B′, ∴△ABC∽△A′B′C′
3.相似三角形的性质:(1)相似三角形的对应角⑦ ,对应边⑧ .(2)相似三角形对应高、对应中线与对应角平分线的比都等于相似比.(3)相似三角形周长的比等于⑨ .(4)相似三角形面积的比等于⑩ .
简记:相似三角形,对应角相等,对应线段成比例.
【特别提示】“两个三角形相似”与“∽”是不同的.若题中只说“两个三角形相似”,那么对应边(角)都不确定,若题中说“相似于(∽)”,则对应边(角)确定.
判定三角形相似的思路:(1)有平行线截线,用平行线的性质找等角;(2)有一对等角,找另一对等角或两邻边对应成比例;(3)有两边对应成比例,找夹角相等或第三边也对应成比例.
考点4.相似三角形的实际应用
1.运用相似三角形解决实际问题:如利用光的反射定律求物体的高度,利用影长计算建筑物的高度、路灯的高度;在同一时刻,物高和影长成比例,即=.
2.运用相似三角形解决实际问题的步骤:(1)根据实际问题建立三角形模型;(2)找出相似三角形;(3)根据相似三角形的性质,表示出相应的量,并求解.
考点5.相似多边形
1.概念:两个边数相同的多边形,如果它们对应角分别相等,对应边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
2.性质:(1)相似多边形的对应角 ,对应边的比等于相似比.(2)相似多边形对应对角线的比、对应边上的高线之比、对应边上的中线之比、对应角的平分线之比都等于相似比.(3)相似多边形的周长之比等于相似比.(4)相似多边形的面积之比等于相似比的 .
【预学习考点巩固专练】
考点巩固专练1:平行线分线段成比例
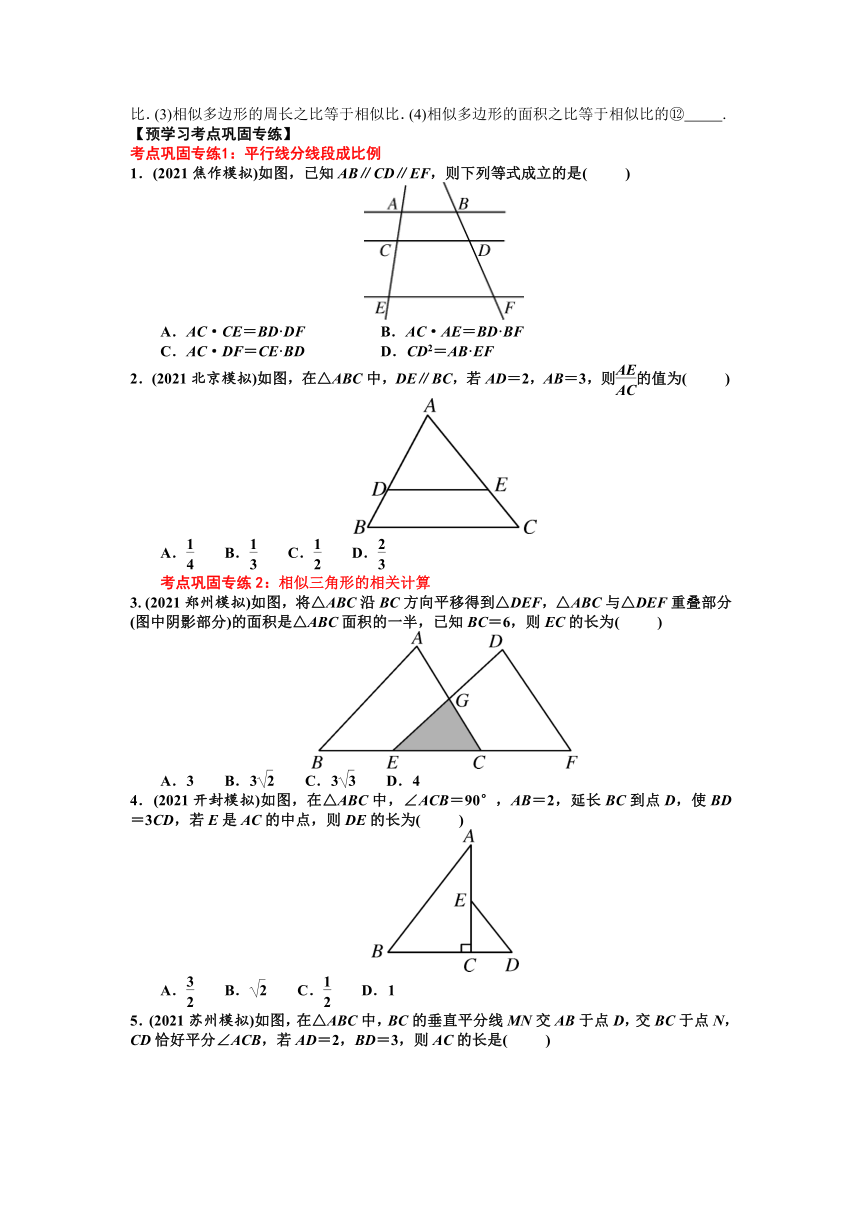
1.(2021焦作模拟)如图,已知AB∥CD∥EF,则下列等式成立的是( )
A.AC·CE=BD·DF B.AC·AE=BD·BF
C.AC·DF=CE·BD D.CD2=AB·EF
2.(2021北京模拟)如图,在△ABC中,DE∥BC,若AD=2,AB=3,则的值为( )
A. B. C. D.
考点巩固专练2:相似三角形的相关计算
3.(2021郑州模拟)如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC面积的一半,已知BC=6,则EC的长为( )
A.3 B.3 C.3 D.4
4.(2021开封模拟)如图,在△ABC中,∠ACB=90°,AB=2,延长BC到点D,使BD=3CD,若E是AC的中点,则DE的长为( )
A. B. C. D.1
5.(2021苏州模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,交BC于点N,CD恰好平分∠ACB,若AD=2,BD=3,则AC的长是( )
A. B.3 C.2 D.6
6.(2021商丘模拟)如图,在等边三角形ABC中,BC=6,BD=2,点P是边BC上一动点(不与端点重合),作∠DPE=60°,PE交边AC于点E.若CE=,则BP的长为( )
A.4 B.2 C.3 D.4或2
7.(2021北京模拟)如图所示的网格是正方形网格,A,B,C是网格线的交点,D,E是AC,BC与网格线的交点,若小正方形的边长为1,则DE的长为 .
8.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=15,点E在边CB上,CE=2EB,点D在边AB上,CD⊥AE,垂足为F,则AD的长为
.
【预学习考点真题回顾】
历年考情分析解读:相似三角形是河南中考的必考内容,但很少单独出题考查,多作为解题的重要工具使用,常应用于复杂几何图形的计算、与圆有关的计算与证明以及几何图形的类比探究综合题等.
命题点:相似三角形的判定与性质
如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
【河南历年中考备用卷试题精选】
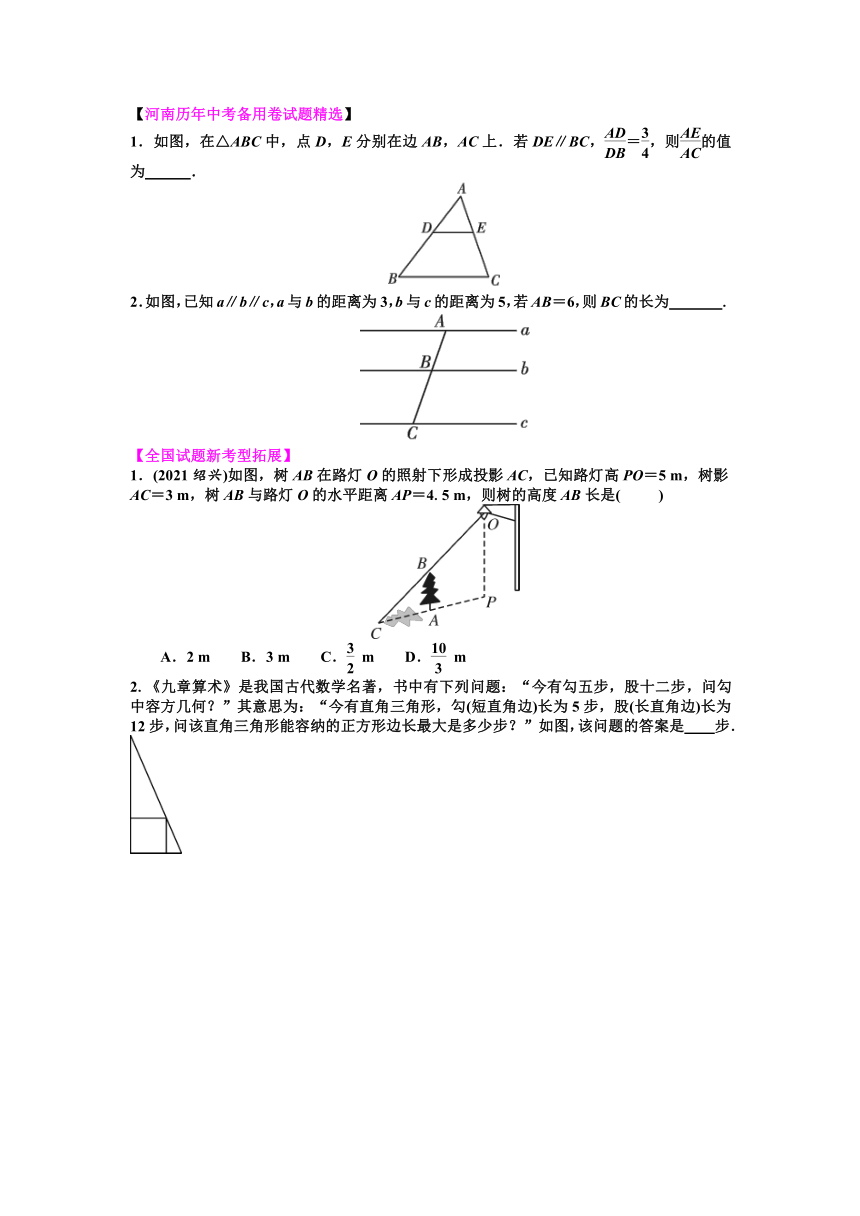
1.如图,在△ABC中,点D,E分别在边AB,AC上.若DE∥BC,=,则的值为 .
2.如图,已知a∥b∥c,a与b的距离为3,b与c的距离为5,若AB=6,则BC的长为 .
【全国试题新考型拓展】
1.(2021绍兴)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB长是( )
A.2 m B.3 m C. m D. m
2.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”如图,该问题的答案是 步.
2022年河南省中考数学总复习
寒假阶段考点解析
第四章 三角形
第7节 相似三角形
【预学习内容课本范围】人教:九下P23~P46
【预学习目标定位导航】
1 了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割;
2 掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;
3 了解相似三角形的性质定理和判定定理;
4 通过具体实例认识图形的相似,了解相似多边形和相似比;
5 会利用图形的相似解决一些简单的实际问题;
6 了解相似三角形判定定理的证明;
7 了解图形的位似,知道利用位似可以将一个图形放大或缩小;
8 在直角坐标系中,探索并了解将一个多边形的顶点坐标(有一个顶点为原点、有一条边在横坐标轴上)分别扩大或缩小相同倍数时所对应的图形与原图形是位似的.
【预学习考点解读分析】
考点1.比例及其性质
1.定义:两个比相等的式子叫做比例,比如=.
2.基本性质:= ① ad=bc .(a,b,c,d都不等于0)
3.合比性质:= =② .(bd≠0)
4.等比性质:==…=(b+d+…+n≠0) =③ .
5.平行线分线段成比例
定理:两条直线被一组平行线所截,所得的对应线段成比例.
如图,由l1∥l2∥l3,可得:
(1)=;(2)=④ ;(3)= .
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
【特别提示】求两条线段的比时,要统一长度单位.
考点2.黄金分割:把一条线段分成两条线段,使较长的线段是原线段与较短的线段的比例中项,叫做把这条线段黄金分割.如图,在线段AB上,点C把线段AB分成两条线段AC和BC(AC>BC),如果=,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,且黄金比为=≈0.618.
【特别提示】一条线段的黄金分割点有2个.
考点3.相似三角形的判定与性质:
1.相似的概念:(1)定义:三个角分别相等,三条边成比例的两个三角形叫做相似三角形.(2)相似比:相似三角形对应边的比叫做相似比(或叫做相似系数).特别地,当相似比等于1时,两个三角形全等.
2.相似三角形的判定
文字描述 图形示例 几何语言
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似 ∵DE∥BC, ∴△ADE∽△ABC
三边⑤ 对应成比例 ,两个三角形相似 ∵==, ∴△ABC∽△A′B′C′
两边对应成比例,且夹角⑥ 相等 的两个三角形相似 ∵=, ∠B=∠B′, ∴△ABC∽△A′B′C′
两角对应相等,两个三角形相似 ∵∠A=∠A′, ∠B=∠B′, ∴△ABC∽△A′B′C′
3.相似三角形的性质:(1)相似三角形的对应角⑦ 相等 ,对应边⑧ 成比例 .(2)相似三角形对应高、对应中线与对应角平分线的比都等于相似比.(3)相似三角形周长的比等于⑨ 相似比 .(4)相似三角形面积的比等于⑩ 相似比的平方 .
简记:相似三角形,对应角相等,对应线段成比例.
【特别提示】“两个三角形相似”与“∽”是不同的.若题中只说“两个三角形相似”,那么对应边(角)都不确定,若题中说“相似于(∽)”,则对应边(角)确定.
判定三角形相似的思路:(1)有平行线截线,用平行线的性质找等角;(2)有一对等角,找另一对等角或两邻边对应成比例;(3)有两边对应成比例,找夹角相等或第三边也对应成比例.
考点4.相似三角形的实际应用
1.运用相似三角形解决实际问题:如利用光的反射定律求物体的高度,利用影长计算建筑物的高度、路灯的高度;在同一时刻,物高和影长成比例,即=.
2.运用相似三角形解决实际问题的步骤:(1)根据实际问题建立三角形模型;(2)找出相似三角形;(3)根据相似三角形的性质,表示出相应的量,并求解.
考点5.相似多边形
1.概念:两个边数相同的多边形,如果它们对应角分别相等,对应边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
2.性质:(1)相似多边形的对应角 相等 ,对应边的比等于相似比.(2)相似多边形对应对角线的比、对应边上的高线之比、对应边上的中线之比、对应角的平分线之比都等于相似比.(3)相似多边形的周长之比等于相似比.(4)相似多边形的面积之比等于相似比的 平方 .
【预学习考点巩固专练】
考点巩固专练1:平行线分线段成比例
1.(2021焦作模拟)如图,已知AB∥CD∥EF,则下列等式成立的是( C )
A.AC·CE=BD·DF B.AC·AE=BD·BF
C.AC·DF=CE·BD D.CD2=AB·EF
2.(2021北京模拟)如图,在△ABC中,DE∥BC,若AD=2,AB=3,则的值为( D )
A. B. C. D.
考点巩固专练2:相似三角形的相关计算
3.(2021郑州模拟)如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC面积的一半,已知BC=6,则EC的长为( B )
A.3 B.3 C.3 D.4
4.(2021开封模拟)如图,在△ABC中,∠ACB=90°,AB=2,延长BC到点D,使BD=3CD,若E是AC的中点,则DE的长为( D )
A. B. C. D.1
5.(2021苏州模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,交BC于点N,CD恰好平分∠ACB,若AD=2,BD=3,则AC的长是( A )
A. B.3 C.2 D.6
6.(2021商丘模拟)如图,在等边三角形ABC中,BC=6,BD=2,点P是边BC上一动点(不与端点重合),作∠DPE=60°,PE交边AC于点E.若CE=,则BP的长为( C )
A.4 B.2 C.3 D.4或2
7.(2021北京模拟)如图所示的网格是正方形网格,A,B,C是网格线的交点,D,E是AC,BC与网格线的交点,若小正方形的边长为1,则DE的长为 2 .
8.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=15,点E在边CB上,CE=2EB,点D在边AB上,CD⊥AE,垂足为F,则AD的长为
9 .
【预学习考点真题回顾】
历年考情分析解读:相似三角形是河南中考的必考内容,但很少单独出题考查,多作为解题的重要工具使用,常应用于复杂几何图形的计算、与圆有关的计算与证明以及几何图形的类比探究综合题等.
命题点:相似三角形的判定与性质
(2015河南第10题,3分)如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
【河南历年中考备用卷试题精选】
1.如图,在△ABC中,点D,E分别在边AB,AC上.若DE∥BC,=,则的值为 .
2.如图,已知a∥b∥c,a与b的距离为3,b与c的距离为5,若AB=6,则BC的长为 10 .
【全国试题新考型拓展】
1.(2021绍兴)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB长是( A )
A.2 m B.3 m C. m D. m
2.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”如图,该问题的答案是 步.
寒假阶段考点解析
第四章 三角形
第7节 相似三角形
【预学习内容课本范围】人教:九下P23~P46
【预学习目标定位导航】
1 了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割;
2 掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;
3 了解相似三角形的性质定理和判定定理;
4 通过具体实例认识图形的相似,了解相似多边形和相似比;
5 会利用图形的相似解决一些简单的实际问题;
6 了解相似三角形判定定理的证明;
7 了解图形的位似,知道利用位似可以将一个图形放大或缩小;
8 在直角坐标系中,探索并了解将一个多边形的顶点坐标(有一个顶点为原点、有一条边在横坐标轴上)分别扩大或缩小相同倍数时所对应的图形与原图形是位似的.
【预学习考点解读分析】
考点1.比例及其性质
1.定义:两个比相等的式子叫做比例,比如=.
2.基本性质:= .(a,b,c,d都不等于0)
3.合比性质:= =② .(bd≠0)
4.等比性质:==…=(b+d+…+n≠0) =③ .
5.平行线分线段成比例
定理:两条直线被一组平行线所截,所得的对应线段成比例.
如图,由l1∥l2∥l3,可得:
(1)=;(2)=④ ;(3)= .
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
【特别提示】求两条线段的比时,要统一长度单位.
考点2.黄金分割:把一条线段分成两条线段,使较长的线段是原线段与较短的线段的比例中项,叫做把这条线段黄金分割.如图,在线段AB上,点C把线段AB分成两条线段AC和BC(AC>BC),如果=,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,且黄金比为=≈0.618.
【特别提示】一条线段的黄金分割点有2个.
考点3.相似三角形的判定与性质:
1.相似的概念:(1)定义:三个角分别相等,三条边成比例的两个三角形叫做相似三角形.(2)相似比:相似三角形对应边的比叫做相似比(或叫做相似系数).特别地,当相似比等于1时,两个三角形全等.
2.相似三角形的判定
文字描述 图形示例 几何语言
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似 ∵DE∥BC, ∴△ADE∽△ABC
三边⑤ ,两个三角形相似 ∵==, ∴△ABC∽△A′B′C′
两边对应成比例,且夹角⑥ 的两个三角形相似 ∵=, ∠B=∠B′, ∴△ABC∽△A′B′C′
两角对应相等,两个三角形相似 ∵∠A=∠A′, ∠B=∠B′, ∴△ABC∽△A′B′C′
3.相似三角形的性质:(1)相似三角形的对应角⑦ ,对应边⑧ .(2)相似三角形对应高、对应中线与对应角平分线的比都等于相似比.(3)相似三角形周长的比等于⑨ .(4)相似三角形面积的比等于⑩ .
简记:相似三角形,对应角相等,对应线段成比例.
【特别提示】“两个三角形相似”与“∽”是不同的.若题中只说“两个三角形相似”,那么对应边(角)都不确定,若题中说“相似于(∽)”,则对应边(角)确定.
判定三角形相似的思路:(1)有平行线截线,用平行线的性质找等角;(2)有一对等角,找另一对等角或两邻边对应成比例;(3)有两边对应成比例,找夹角相等或第三边也对应成比例.
考点4.相似三角形的实际应用
1.运用相似三角形解决实际问题:如利用光的反射定律求物体的高度,利用影长计算建筑物的高度、路灯的高度;在同一时刻,物高和影长成比例,即=.
2.运用相似三角形解决实际问题的步骤:(1)根据实际问题建立三角形模型;(2)找出相似三角形;(3)根据相似三角形的性质,表示出相应的量,并求解.
考点5.相似多边形
1.概念:两个边数相同的多边形,如果它们对应角分别相等,对应边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
2.性质:(1)相似多边形的对应角 ,对应边的比等于相似比.(2)相似多边形对应对角线的比、对应边上的高线之比、对应边上的中线之比、对应角的平分线之比都等于相似比.(3)相似多边形的周长之比等于相似比.(4)相似多边形的面积之比等于相似比的 .
【预学习考点巩固专练】
考点巩固专练1:平行线分线段成比例
1.(2021焦作模拟)如图,已知AB∥CD∥EF,则下列等式成立的是( )
A.AC·CE=BD·DF B.AC·AE=BD·BF
C.AC·DF=CE·BD D.CD2=AB·EF
2.(2021北京模拟)如图,在△ABC中,DE∥BC,若AD=2,AB=3,则的值为( )
A. B. C. D.
考点巩固专练2:相似三角形的相关计算
3.(2021郑州模拟)如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC面积的一半,已知BC=6,则EC的长为( )
A.3 B.3 C.3 D.4
4.(2021开封模拟)如图,在△ABC中,∠ACB=90°,AB=2,延长BC到点D,使BD=3CD,若E是AC的中点,则DE的长为( )
A. B. C. D.1
5.(2021苏州模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,交BC于点N,CD恰好平分∠ACB,若AD=2,BD=3,则AC的长是( )
A. B.3 C.2 D.6
6.(2021商丘模拟)如图,在等边三角形ABC中,BC=6,BD=2,点P是边BC上一动点(不与端点重合),作∠DPE=60°,PE交边AC于点E.若CE=,则BP的长为( )
A.4 B.2 C.3 D.4或2
7.(2021北京模拟)如图所示的网格是正方形网格,A,B,C是网格线的交点,D,E是AC,BC与网格线的交点,若小正方形的边长为1,则DE的长为 .
8.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=15,点E在边CB上,CE=2EB,点D在边AB上,CD⊥AE,垂足为F,则AD的长为
.
【预学习考点真题回顾】
历年考情分析解读:相似三角形是河南中考的必考内容,但很少单独出题考查,多作为解题的重要工具使用,常应用于复杂几何图形的计算、与圆有关的计算与证明以及几何图形的类比探究综合题等.
命题点:相似三角形的判定与性质
如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
【河南历年中考备用卷试题精选】
1.如图,在△ABC中,点D,E分别在边AB,AC上.若DE∥BC,=,则的值为 .
2.如图,已知a∥b∥c,a与b的距离为3,b与c的距离为5,若AB=6,则BC的长为 .
【全国试题新考型拓展】
1.(2021绍兴)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB长是( )
A.2 m B.3 m C. m D. m
2.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”如图,该问题的答案是 步.
2022年河南省中考数学总复习
寒假阶段考点解析
第四章 三角形
第7节 相似三角形
【预学习内容课本范围】人教:九下P23~P46
【预学习目标定位导航】
1 了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割;
2 掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例;
3 了解相似三角形的性质定理和判定定理;
4 通过具体实例认识图形的相似,了解相似多边形和相似比;
5 会利用图形的相似解决一些简单的实际问题;
6 了解相似三角形判定定理的证明;
7 了解图形的位似,知道利用位似可以将一个图形放大或缩小;
8 在直角坐标系中,探索并了解将一个多边形的顶点坐标(有一个顶点为原点、有一条边在横坐标轴上)分别扩大或缩小相同倍数时所对应的图形与原图形是位似的.
【预学习考点解读分析】
考点1.比例及其性质
1.定义:两个比相等的式子叫做比例,比如=.
2.基本性质:= ① ad=bc .(a,b,c,d都不等于0)
3.合比性质:= =② .(bd≠0)
4.等比性质:==…=(b+d+…+n≠0) =③ .
5.平行线分线段成比例
定理:两条直线被一组平行线所截,所得的对应线段成比例.
如图,由l1∥l2∥l3,可得:
(1)=;(2)=④ ;(3)= .
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
【特别提示】求两条线段的比时,要统一长度单位.
考点2.黄金分割:把一条线段分成两条线段,使较长的线段是原线段与较短的线段的比例中项,叫做把这条线段黄金分割.如图,在线段AB上,点C把线段AB分成两条线段AC和BC(AC>BC),如果=,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,且黄金比为=≈0.618.
【特别提示】一条线段的黄金分割点有2个.
考点3.相似三角形的判定与性质:
1.相似的概念:(1)定义:三个角分别相等,三条边成比例的两个三角形叫做相似三角形.(2)相似比:相似三角形对应边的比叫做相似比(或叫做相似系数).特别地,当相似比等于1时,两个三角形全等.
2.相似三角形的判定
文字描述 图形示例 几何语言
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似 ∵DE∥BC, ∴△ADE∽△ABC
三边⑤ 对应成比例 ,两个三角形相似 ∵==, ∴△ABC∽△A′B′C′
两边对应成比例,且夹角⑥ 相等 的两个三角形相似 ∵=, ∠B=∠B′, ∴△ABC∽△A′B′C′
两角对应相等,两个三角形相似 ∵∠A=∠A′, ∠B=∠B′, ∴△ABC∽△A′B′C′
3.相似三角形的性质:(1)相似三角形的对应角⑦ 相等 ,对应边⑧ 成比例 .(2)相似三角形对应高、对应中线与对应角平分线的比都等于相似比.(3)相似三角形周长的比等于⑨ 相似比 .(4)相似三角形面积的比等于⑩ 相似比的平方 .
简记:相似三角形,对应角相等,对应线段成比例.
【特别提示】“两个三角形相似”与“∽”是不同的.若题中只说“两个三角形相似”,那么对应边(角)都不确定,若题中说“相似于(∽)”,则对应边(角)确定.
判定三角形相似的思路:(1)有平行线截线,用平行线的性质找等角;(2)有一对等角,找另一对等角或两邻边对应成比例;(3)有两边对应成比例,找夹角相等或第三边也对应成比例.
考点4.相似三角形的实际应用
1.运用相似三角形解决实际问题:如利用光的反射定律求物体的高度,利用影长计算建筑物的高度、路灯的高度;在同一时刻,物高和影长成比例,即=.
2.运用相似三角形解决实际问题的步骤:(1)根据实际问题建立三角形模型;(2)找出相似三角形;(3)根据相似三角形的性质,表示出相应的量,并求解.
考点5.相似多边形
1.概念:两个边数相同的多边形,如果它们对应角分别相等,对应边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
2.性质:(1)相似多边形的对应角 相等 ,对应边的比等于相似比.(2)相似多边形对应对角线的比、对应边上的高线之比、对应边上的中线之比、对应角的平分线之比都等于相似比.(3)相似多边形的周长之比等于相似比.(4)相似多边形的面积之比等于相似比的 平方 .
【预学习考点巩固专练】
考点巩固专练1:平行线分线段成比例
1.(2021焦作模拟)如图,已知AB∥CD∥EF,则下列等式成立的是( C )
A.AC·CE=BD·DF B.AC·AE=BD·BF
C.AC·DF=CE·BD D.CD2=AB·EF
2.(2021北京模拟)如图,在△ABC中,DE∥BC,若AD=2,AB=3,则的值为( D )
A. B. C. D.
考点巩固专练2:相似三角形的相关计算
3.(2021郑州模拟)如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC面积的一半,已知BC=6,则EC的长为( B )
A.3 B.3 C.3 D.4
4.(2021开封模拟)如图,在△ABC中,∠ACB=90°,AB=2,延长BC到点D,使BD=3CD,若E是AC的中点,则DE的长为( D )
A. B. C. D.1
5.(2021苏州模拟)如图,在△ABC中,BC的垂直平分线MN交AB于点D,交BC于点N,CD恰好平分∠ACB,若AD=2,BD=3,则AC的长是( A )
A. B.3 C.2 D.6
6.(2021商丘模拟)如图,在等边三角形ABC中,BC=6,BD=2,点P是边BC上一动点(不与端点重合),作∠DPE=60°,PE交边AC于点E.若CE=,则BP的长为( C )
A.4 B.2 C.3 D.4或2
7.(2021北京模拟)如图所示的网格是正方形网格,A,B,C是网格线的交点,D,E是AC,BC与网格线的交点,若小正方形的边长为1,则DE的长为 2 .
8.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=15,点E在边CB上,CE=2EB,点D在边AB上,CD⊥AE,垂足为F,则AD的长为
9 .
【预学习考点真题回顾】
历年考情分析解读:相似三角形是河南中考的必考内容,但很少单独出题考查,多作为解题的重要工具使用,常应用于复杂几何图形的计算、与圆有关的计算与证明以及几何图形的类比探究综合题等.
命题点:相似三角形的判定与性质
(2015河南第10题,3分)如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
【河南历年中考备用卷试题精选】
1.如图,在△ABC中,点D,E分别在边AB,AC上.若DE∥BC,=,则的值为 .
2.如图,已知a∥b∥c,a与b的距离为3,b与c的距离为5,若AB=6,则BC的长为 10 .
【全国试题新考型拓展】
1.(2021绍兴)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB长是( A )
A.2 m B.3 m C. m D. m
2.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”如图,该问题的答案是 步.
同课章节目录
